このページでは、インボリューション行列とは何かを学びます。また、次元 2×2、3×3、および 4×4 のインボリューティブ行列の例も示します。そして最後に、累積行列の公式を見つけます。
累積行列とは何ですか?
累積行列の意味は次のとおりです。
インボリューティブ行列の定義 : 逆行列が行列そのものである可逆正方行列。
![]()
金
![]()
は任意の行列であり、
![]()
はその逆を表します。
したがって、明らかに、畳み込み行列は、正規行列または非縮退行列の一例です。
行列の逆行列がわからない場合は、ここで3×3 逆行列の計算方法を参照してください。逆行列の方法を知ることは重要ですが、そのためには行列の随伴がどのように計算されるかを知る必要もあります。
しかし、本題に戻ります。行列が包含的である場合、行列と行列自体を乗算すると単位行列が得られます。デモを見てみましょう:
行列にその逆行列を乗算すると、アイデンティティ (またはユニット) 行列が得られます。それで:
![]()
そして、インボリューション行列の逆行列は行列そのものであるため、次のようになります。
![]()
したがって、平方インボリューション行列は単位行列を与えます。
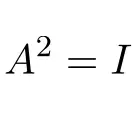
インボリューション行列の例
2×2 積分行列の例:
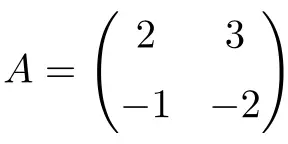
行列の 2 乗を計算することで、それがインボリューション行列であることを確認できます。
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-314aebadfe3da501264c0eb14e1dfc2f_l3.png)
行列 A の 2 乗は恒等行列であるため、行列 A は 2×2 の累積行列になります。
3×3 の積分行列の例:
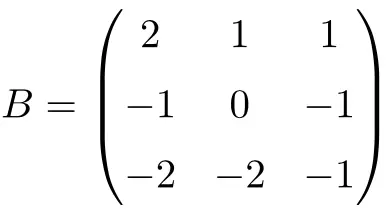
行列の積を単独で解くことで、それが累積行列であることを検証できます。
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-599241f00e8a89f8b55ed2ae8cb42ddb_l3.png)
行列 B の 2 乗は単位行列であるため、行列 B は 3×3 の累積行列になります。
4×4 の積分行列の例:
Identity (または Unit) 行列は、その次元が何であれ、定義上、インボリューショナル行列です。
![Rendered by QuickLaTeX.com \displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4278c2b46761d3b258eb9ba04c87bbf1_l3.png)
行列を 2 に増やすことで、それが累積行列であることを確認できます。
![Rendered by QuickLaTeX.com \displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3190f24d196c4b96a60ec06fe7180e6_l3.png)
二乗単位行列は単位行列なので、単位行列は 4×4 の累積行列になります。
明らかに、単位行列は、主対角がすべて 1 で残りが 0 の単純な対角行列であるため、任意の次元にすることができます。したがって、単位行列は、その順序に関係なく、常にインボリューション行列になります。
畳み込み行列の公式
インボリューション行列の特性の 1 つは、その式が既知であることです。ただし、2 次の累積行列の公式の証明は非常に面倒なので、結果についてはそのままにしておきます。それが本当に重要です。デモに興味がある場合は、以下のコメントで段階的に説明されています。
2 × 2 次元のインボリューティブ行列の式は次のとおりです。

したがって、主対角値が反対で、行列式が -1 である行列は、累積行列になります。
ただし、この式で記述される行列に加えて、単位行列とその逆行列も次数 2 の累積行列であることを考慮する必要があります。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-395beb5a766a10eefa56a087e8c8d098_l3.png)
インボリューション行列のプロパティ
インボリューション行列には次の特徴があります。
- 累積行列の行列式は常に -1 または +1 に等しくなります。
- 累積行列と冪等行列の間には関係があります:行列

行列が次の場合に限り、累積的です。
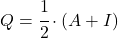
べき等です。
- うん

そして

2 つの可換累積行列であり、行列積
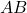
も別のインボリューション行列です。
- 累積行列の累乗は、別の累積行列になります。特に、奇数の指数に累乗されたインボリューション行列はそれ自体と等しくなりますが、一方、偶数の指数に累乗された場合は恒等行列と等価になります。
![]()
![]()