このページでは、空間における解析幾何学 (および公式) に関するすべての説明が見つかります。直線と平面の方程式、平面と直線の間の相対位置、空間での距離と角度の計算方法などです。
空間における幾何学とは何ですか?
空間幾何学は、三次元 (3D) 幾何学図形、つまり空間内の場所を占める幾何学図形の研究を担当する幾何学の分野です。円錐、立方体、角錐、球、円柱、角柱、多面体など。
ただし、このページでは、点、線、平面、2 つの幾何学的図形の間の距離、それらが形成する角度、異なる幾何学間の交点の分析に焦点を当てる空間幾何学の一部である、空間における解析幾何学に焦点を当てます。数字。要素など
空間内の直線の方程式
線の数学的定義は、曲線や角度を持たずに同じ方向に表現された一連の点であることを思い出してください。
したがって、(R3 で) 3 次元空間内の任意の線を数学的に表現するには、線の方程式を使用します。それらを見つけるには、線に属する点とその線の方向ベクトルのみが必要です。

これら 2 つの幾何学的要素だけを使用すると、次のような直線のさまざまな方程式をすべて見つけることができます。
直線の方程式は、ベクトル方程式、パラメトリック方程式、連続方程式、および陰的 (または一般) 方程式です。
以下に、さまざまなタイプの直線の方程式について説明します。
空間内の直線のベクトル方程式
うん
![]()
は直線の方向ベクトルであり、
![]()
右側に属する点:
![]()
直線のベクトル方程式の式は次のとおりです。
![]()
空間内の線のパラメトリック方程式
コンポーネントをコンポーネントと等しくすることで、ベクトル方程式から線のパラメトリック方程式の式を取得できます。
![]()
空間内の直線の連続方程式
直線の連続方程式の公式は次のとおりです。
![]()
このタイプの直線方程式はパラメトリック方程式からも取得できます。連続方程式のページでデモをご覧いただけます。さらに、右側から方程式の例を見て、解いた演習で練習することもできます。
空間内の直線の一般 (または暗黙の) 方程式
最後に、直線の連続方程式の分数を 2 で乗算することにより、直線の一般 (または陰的) 方程式が得られます。
![]()
このタイプの直線の方程式は、デカルト方程式とも呼ばれます。
最も関連性の高い直線の 4 つの方程式 (ベクトル、パラメトリック、連続、および一般) を見てきましたが、少し特殊な方程式がもう 1 つあるため、それを説明するには 1 ページかかります。これは正準方程式です。このリンクでは、その説明全体、なぜそれが特別なのか、他の方程式と何が違うのかを見ることができます。
空間における平面方程式
解析幾何学において、平面の方程式は、任意の平面を解析的に表現できる方程式です。したがって、平面の方程式を見つけるには、1 つの点と、その平面に属する 2 つの線形に独立したベクトルのみが必要です。

したがって、平面のすべてのタイプの方程式は、平面のベクトル方程式、パラメトリック方程式、陰的 (または一般) 方程式、および正準 (または部分) 方程式です。
次に、計画のすべての方程式の説明と式を見ていきます。
平面のベクトル方程式
点と平面の 2 つの方向ベクトルが与えられると、次のようになります。
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
平面のベクトル方程式の公式は次のとおりです。
![]()
または同等のもの:
![]()
金
![]()
そして
![]()
これらは 2 つのスカラー、つまり 2 つの実数です。
平面のパラメトリック方程式
一方、平面のパラメトリック方程式の公式は次のとおりです。
![]()
平面の暗黙的または一般方程式
計画の暗黙的な方程式は、一般方程式とも呼ばれ、次の行列式を解き、結果を 0 に設定することによって取得されます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
したがって、結果として得られる計画の暗黙的方程式または一般方程式は次の形式になります。
![]()
このタイプの平面方程式は、デカルト平面方程式とも呼ばれます。
平面の正準方程式または部分方程式
平面の正準方程式または部分方程式の式は次のとおりです。
![]()
金:
-

これは、平面と X 軸の交点です。
-

これは、平面と Y 軸の交点です。
-

これは、平面が Z 軸と交差する場所です。
平面に垂直なベクトル
平面に垂直なベクトルは、この平面に含まれるすべての線に垂直なベクトルです。したがって、平面に垂直なベクトルは、平面に垂直であることを意味します。
空間解析幾何学における計量問題の多くは、平面とその法線ベクトルに関係します。これらの演習を解決するには、平面とその法線ベクトルの間の数学的関係を知る必要があるだけです。
平面に垂直なベクトルの成分 X、Y、Z は、それぞれ前記平面の陰的な (または一般的な) 方程式の係数 A、B、C と一致します。
![]()
金
![]()
平面に直交するベクトルです
![]()
空間内の 2 つの幾何学的要素の相対位置
明らかに、線や平面は必ずしも空間内に単独で存在する必要はありませんが、逆に、通常は互いに影響し合います。交差したり、平行したり、垂直になったりします。さて、このセクションでは、線と平面のさまざまな相対位置と、それらがどのように決定されるかを見ていきます。
空間内の 2 つの線の相対位置
解析幾何学では、3 次元空間 (R3) で作業する場合、2 つの線の間には 4 つの相対位置が考えられます。2 つの線は、一致線、平行線、割線、または割線になります。
平行線

2 本の線は、方向が同じでも共通点がない場合、平行です。さらに、平行線は常に互いに同じ距離にあります。
一致する線

2 本の線が同じ方向を持ち、すべての点が共通している場合、2 本の線は一致します。
交線

交差する 2 つの線は方向が異なりますが、1 点で接触します。
交線

交差する 2 つの線は方向が異なり、どの点でも交差しません。したがって、2 つの交差した線は同じ平面上にありません。たとえば、線の上のグラフィック表現では、
![]()
いつも直線の先にある
![]()
, したがって、彼らは決してお互いに触れることはありません。
範囲によって 2 つの線の相対位置を見つける方法
2 つの行の相対位置を見つける 1 つの方法は、以下に示すように、2 つの特定の行列の範囲を計算することです。この方法は、2 つの直線が陰的な (または一般的な) 方程式の形式で表現される場合に非常に役立ちます。
したがって、3 次元空間 (R3) で暗黙的な (または一般的な) 方程式で表現された 2 つの直線があるとします。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-500405383e97627c17d01023fd9dd198_l3.png)
![Rendered by QuickLaTeX.com \displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c96b6990dae5ce476ee55689cf4f4fb_l3.png)
A を 2 つのラインの係数で構成される行列とします。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9199790c5f157691d9307604f25fc873_l3.png)
そして、展開された行列 A’ を考えると、これは 2 つの行のすべてのパラメータで構成される行列です。
![Rendered by QuickLaTeX.com \displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f087aea2d9209341c2acf240eab2bc77_l3.png)
次に、2 つの線の相対位置は、次の表に従って、前の 2 つの行列の範囲によって決定できます。

したがって、2 つの行間の相対位置を見つけるには、両方の行列の範囲を計算する必要があり、各行列の範囲に応じてどちらかの場合が決まります。
この定理はルーシェ-フロベニウスの定理 (連立一次方程式を解くために使用される方法) を使用して証明できますが、非常に面倒であまり追加しないため、このページでは証明を行いません。 。
空間内の 2 つの平面の相対位置
解析幾何学では、2 つの平面間に可能な相対位置は、交差する平面、平行な平面、一致する平面の 3 つだけです。
- 交差する平面: 2 つの平面が 1 つの線上でのみ交差する場合、2 つの平面は交差しています。
- 平行平面: 2 つの平面は、どの点でも交差しなければ平行です。
- 一致する平面: 2 つの平面は、すべての点が共通している場合に一致します。
交差するショット

平行面

マッチングプラン

係数によって 2 つの平面の相対位置を決定する方法
2 つの平面間の相対位置を知る 1 つの方法は、一般 (または暗黙的な) 方程式の係数を使用することです。
次に、2 つの異なる平面の一般 (または暗黙の) 方程式を考えてみましょう。
![]()
![]()
3 次元空間における 2 つの平面間の相対位置は、それらの係数またはパラメーターの比例性に依存します。

したがって、係数 A、B、または C のいずれかが他の係数に比例しない場合、2 つの平面は交差します。一方、独立項のみが比例しない場合、2 つの平面は平行になります。そして最後に、2 つの方程式の係数がすべて比例する場合、計画は一致します。
空間内の距離
以下は、点と線の間、2 つの平面の間、平面と線の間など、さまざまな幾何学的要素間の距離を計算する式です。
2 点間の距離
2 点間の距離は、これら 2 点によって決定されるベクトルのノルムに対応します。
したがって、2 つの一般的な点があるとします。
![]()
2 点間の距離の公式は次のとおりです。
![]()
点から線までの距離
空間内の点から線までの距離を計算する式は次のとおりです。
![]()
金:
-

線の方向ベクトルのモジュールです

-

右側の点です


線上の点

そして

2 つの点によって定義されるベクトル
-

ベクトル間のベクトル積の係数です。

そして

2本の線の間の距離
2 つの線の間の距離は、それらの相対位置によって異なります。
- 2 つの線が一致するか交差する場合、2 つの線は (少なくとも) 1 点で交差するため、2 つの線の間の距離はゼロに等しくなります。
- 2 本の線が平行または交差している場合は、場合に応じて公式を適用する必要があります (両方の説明は以下で参照できます)。
2 本の平行線の間の距離
2 本の平行線は常に同じ距離離れています。したがって、空間内 (R3) の 2 本の平行線の間の距離を計算するには、平面 (R2) での場合と同じ方法で行います。必要なのは、2 本の線のうちの 1 つの上の点を取り、そこにある距離を見つけることだけです。は、この点から他の行までです。

したがって、2 本の平行線の間の距離を決定するには、点と線の間の距離の公式を使用する必要があります。
交差する 2 本の線の間の距離
方向ベクトルと 2 つの交差する線の任意の点を次のようにします。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-569f8d554a0f3704d247862d0b8ef852_l3.png)
交差する 2 本の線の間の距離の公式は次のとおりです。
![]()
金:
-
![Rendered by QuickLaTeX.com \left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|](https://mathority.org/wp-content/ql-cache/quicklatex.com-dbc3e38427d29b2f4444ea732f955500_l3.png)
ベクトルの混合積の絶対値です。
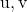
および点によって定義されるベクトル

そして

。
-
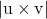
は、2 つの交差した線の方向ベクトル間のベクトル積の係数です。
ここに公式がありますが、交差する 2 つの線の間の距離を決定することは、思っているよりも複雑です。したがって、練習したい場合は、次のリンクで、交差する 2 つの線の間の距離に関する例と解決済みの演習を参照できます。
点から面までの距離
点と平面の一般 (または暗黙の) 方程式が与えられると、次のようになります。
![]()
点から平面までの距離の公式は次のとおりです。
![]()

式を適用してゼロに等しい結果が得られた場合、これは明らかに、点と平面の間の距離がゼロであり、したがって点はこの平面の一部であることを意味します。
2 つの平面間の距離
空間内の 2 つの平面間の距離は、これら 2 つの平面間の相対位置によって異なります。
- 2 つの平面が交差または一致している場合、それらは特定の点で交差するため、それらの間の距離はゼロに等しくなります。
- 2 つの平面が平行である場合、2 つの平面間の距離は、2 つの平面の一方の点を取得し、その点ともう一方の平面の間の距離を計算することによって計算されます。
2 つの平行な平面間の距離
2 つの平行な平面は常に互いに同じ距離にあるため、2 つの平行な平面間の距離を見つけるには、2 つの平面の一方の点を取得し、その点からもう一方の平面までの距離を計算できます。

したがって、2 つの平行な平面間の距離を計算するには、2 つの平面のいずれかで点を見つけて、点と平面の間の距離の公式を使用する必要があります。
空間の角度
距離と同様に、空間内の 2 つの幾何学的オブジェクト間の角度の決定は、それらの幾何学的特性に依存します。 2 本の線によって形成される角度を計算することは、2 つの平面によって形成される角度を計算することと同じではないためです。以下に、線と平面の間の角度を求める公式を示します。
2本の線の間の角度
ユークリッド空間の 2 本の線の間の角度を知るには、それらの方向ベクトルによって形成される角度を計算する必要があります。したがって、次のようになります。
2 つの異なるラインの方向ベクトルを考えると、次のようになります。
![]()
これら 2 つの線によって形成される角度は、次の式で計算できます。
![]()
金
![]()
そして
![]()
ベクトルのモジュールです
![]()
そして
![]()
それぞれ。
ベクトルの係数の公式は次のとおりであることを思い出してください。
![]()
2 つの平面間の角度
2つの平面間の角度は、前記平面の法線ベクトルによって形成される角度に等しい。したがって、 2 つの平面間の角度を見つけるには、それらの法線ベクトルが等価であるため、それらの法線ベクトルによって形成される角度を計算します。
2 つの異なる平面の一般 (または暗黙の) 方程式を考えると、次のようになります。
![]()
![]()
各平面の法線ベクトルは次のとおりです。
![]()
![]()
これら 2 つの平面によって形成される角度は、次の式を使用して法線ベクトルによって形成される角度を計算することによって決定されます。
![]()
線と平面の間の角度
線と平面によって形成される角度は、線の方向ベクトルと平面の法線ベクトルによって形成される 2 つの補角のうち小さい方として定義されます。
したがって、もし
![]()
は直線の方向ベクトルであり、
![]()
は平面に垂直なベクトルです。
![]()
![]()
線と平面によって形成される角度を計算するために使用される公式は次のとおりです。
![]()