直線方程式 -

ここでは、直線のあらゆるタイプの方程式の公式が見つかります。さらに、それらの計算方法の例を確認したり、直線の方程式の演習問題を解いて練習したりすることができます。

直線の方程式はすべて何ですか?

線の数学的定義は、曲線や角度を持たずに同じ方向に表現される一連の連続する点であることに注意してください。

したがって、平面 (R2) 内の直線を解析的に表現するには、直線の方程式を使用します。直線の方程式を求めるには、直線に属する点と、その直線の方向ベクトルのみが必要です。これら 2 つの幾何学的要素だけを使用すると、次のような直線のさまざまな方程式をすべて見つけることができます。

直線の方程式は、ベクトル方程式、パラメトリック方程式、連続方程式、陰的 (または一般) 方程式、陽的方程式、点-傾き方程式、および正準 (または部分) 方程式です。

すべてのタイプの線方程式には、線を数学的に表すという同じ目的があります。ただし、直線の方程式にはそれぞれ特性があるため、問題に応じてどちらかを使用する方がよいでしょう。

直線方程式の概念を理解したら、次に、特に各種類の直線方程式の特性の分析に進みます。以下では、行内のさまざまなタイプの方程式の詳細な説明が示されていますが、必要に応じて、行内のすべての方程式の式を含む概要表の最後に直接移動することもできます。

直線のベクトル方程式

うん

$\vv{\text{v}}$

は直線の方向ベクトルであり、

$P$

右側に属する点:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

直線のベクトル方程式の式は次のとおりです。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2) \end{empheq}$

金：

$x$

そして

$y$

は、線上の任意の点のデカルト座標です。
$P_1$

そして

$P_2$

直線の一部を形成する既知の点の座標です

$P(P}_1,P_2).$
$\text{v}_1$

そして

$\text{v}_2$

線の方向ベクトルの成分です

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

はスカラー (実数) であり、その値は線上の各点に依存します。

これは、平面内の直線のベクトル方程式、つまり 2 つの座標 (R2 内) の点とベクトルを操作する場合です。ただし、空間 (R3) で計算を行っている場合は、直線の方程式に追加のコンポーネントを追加する必要があります。

$(x,y,z)=(P_1,P_2,P_3)+t\cdot (\text{v}_1,\text{v}_2,\text{v}_3)$

直線のパラメトリック方程式

線のパラメトリック方程式は、そのベクトル方程式から取得できます。

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

まずパラメータを乗算します

$t$

右の方向ベクトルによる：

$(x,y)=(P_1,P_2)+ (t\cdot\text{v}_1,t\cdot\text{v}_2)$

次に、X 座標と Y 座標を追加します。

$(x,y)=(P_1+t\cdot\text{v}_1,P_2+t\cdot\text{v}_2)$

そして最後に、各変数を個別にクリアして、次の直線のパラメトリック方程式を取得します。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases} \end{empheq}$

金：

$x$

そして

$y$

は、線上の任意の点のデカルト座標です。
$P_1$

そして

$P_2$

直線の一部を形成する既知の点の座標です

$P(P}_1,P_2).$
$\text{v}_1$

そして

$\text{v}_2$

線の方向ベクトルの成分です

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

はスカラー (実数) であり、その値は線上の各点に依存します。

前と同様、これらは平面 (R2) 内の線のパラメトリック方程式ですが、空間 (R3) 内の線のパラメトリック方程式を見つけるには、3 番目の変数 Z にもう 1 つ方程式を追加する必要があります。

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}$

連続直線方程式

任意の直線の連続方程式は、パラメトリック方程式から推定できます。

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

設定をクリアすると

$t$

各パラメトリック方程式から次の式が得られます。

$t =\cfrac{x-P_1}{\text{v}_1}}$

$t =\cfrac{y-P_2}{\text{v}_2}}$

E 結果として得られる 2 つの方程式を等価すると、直線の連続方程式が得られます。

$t= t$

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

つまり、直線の連続方程式は次のようになります。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2} \end{empheq}$

金：

$x$

そして

$y$

は、線上の任意の点のデカルト座標です。
$P_1$

そして

$P_2$

直線の一部を形成する既知の点の座標です

$P(P}_1,P_2).$
$\text{v}_1$

そして

$\text{v}_2$

線の方向ベクトルの成分です

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$

この公式は、2 次元 (2D) で作業する場合の直線の連続方程式用です。しかし、3 次元 (3D) で演算を実行している場合は、直線方程式に追加のコンポーネントを追加する必要があります。

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}$

暗黙的または一般的な直線の方程式

うん

$\vv{\text{v}}$

は直線の方向ベクトルであり、

$P$

右側に属する点:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

直線の陰的な一般方程式またはデカルト方程式の式は次のとおりです。

金：

$x$

そして

$y$

は、線上の任意の点のデカルト座標です。
係数
$A$

は線の方向ベクトルの 2 番目の成分です。

$A=\text{v}_2}$
係数
$B$

方向ベクトルの最初の成分が符号を変更します。

$B=-\text{v}_1}$
係数
$C$

既知の点を置き換えることによって計算されます

$P$

直線の方程式で。

この公式では、直線の陰的な方程式は、連続方程式の分数を乗算することによっても取得できます。

明示的な直線の方程式

直線の明示的な方程式の式は次のとおりです。

金：

$m$

線の傾きです。
$n$

y 切片、つまり Y 軸と交差する高さです。

以下のセクションでは、パラメータがどのように決定されるかを説明します。

$m$

そして

$n$

しかし、特に、陽的な方程式を見つける別の方法は、陰的な方程式を使用することです。そのためには未知の部分を解決する必要があります

$y$

暗黙的な方程式の。

パラメータ m と n の意味

直線の明示的な方程式の定義で見たように、パラメータは

$m$

は線の傾きであり、

$n$

その y 切片。しかし、それは何を意味するのでしょうか？これを線のグラフィック表現から見てみましょう。

独立という言葉

$\bm{n}$

線とコンピュータ軸 (OY 軸) の交点です。たとえば、上のグラフでは

$n$

直線は y=1 で y 軸と交差するため、は 1 に等しくなります。

一方で、この用語は、

$\bm{m}$

は線の傾き、つまり傾きを示します。グラフからわかるように、

$m$

ラインは 1 水平単位に対して 2 垂直単位ずつ上昇するため、は 2 に等しくなります。

明らかに、傾きが正の場合、関数は増加 (上昇) し、一方、傾きが負の場合、関数は減少 (下降) します。

線の傾きを計算する

線の傾きが正確にわかったら、それがどのように計算されるかを見てみましょう。したがって、線の傾きを数値的に決定するには 3 つの異なる方法があります。

直線上の 2 つの異なる点が与えられると、
$P_1(x_1,y_1)$

そして

$P_2(x_2,y_2),$

線の傾きは次のようになります。

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

うん
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

は線の方向ベクトルであり、その傾きは次のとおりです。

$m = \cfrac{\text{v}_2}{\text{v}_1}$

うん
$\alpha$

は横軸 (X 軸) と線によって形成される角度であり、線の傾きはその角度の正接に相当します。

$m = \text{tg}(\alpha )$

直線の点と傾きの方程式

直線の点と傾きの方程式の式は次のとおりです。

金：

$m$

線の傾きです。
$P_1, P_2$

線上の点の座標です

$P(P_1,P_2).$

直線の正準方程式または部分方程式

この直線の方程式の変形はあまり知られていませんが、直線の正準方程式は直線とデカルト軸の交点から取得できます。

指定された直線の軸との 2 つの交点を次のようにします。

X 軸でカットします。

$(a,0)$

Y 軸でカット:

$(0,b)$

直線の正準方程式の式は次のとおりです。

数学では、直線の正準方程式は部分方程式または対称方程式とも呼ばれます。

一方、係数は

$a$

そして

$b$

これらは、次の式を使用して直線の一般方程式から求めることもできます。

$Ax+By+C=0$

$a = -\cfrac{C}{A} \qquad \qquad b = -\cfrac{C}{B}$

すべての直線の方程式（公式）

要約すると、直線のすべての方程式の公式を示す表が次のとおりです。

直線の方程式の計算例

直線の方程式の全体的な説明を見たところで、直線の方程式の典型的な問題がどのように解決されるかを見てみましょう。

点によって決まる直線の方程式をすべて求めます
$P$

そしてベクトル

$\vv{\text{v}}.$

$P(3,-1) \qquad \qquad \vv{\text{v}}=(2,4)$

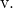
まず第一に、その公式から直線のベクトル方程式を見つけます。

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

点とベクトルの座標を式に代入するだけです。

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(3,-1)+t\cdot (2,4)} \quad \vphantom{\Bigl(}}$

次に、対応する式を通じて線のパラメトリック方程式を見つけます。

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

また、その公式を使用して直線の連続方程式も決定します。

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-3}{2}=\cfrac{y-(-1)}{4}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x-3}}{\bm{2}}\bm{=}\cfrac{\bm{y+1}}{\bm{4}}\quad \vphantom{\Biggl(}}$

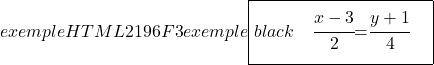
これまで見てきたように、ベクトル、パラメトリック、連続方程式はそれぞれの公式を使用するだけで簡単に計算できます。

次に、直線の一般 (または暗黙の) 方程式を見つけることに移りましょう。これを行うには、連続方程式の 2 つの部分を交差させます。

$4\cdot (x-3)= 2 \cdot (y+1)$

$4x-12= 2y+2$

$4x-12-2y-2=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{4x-2y-14=0}\quad \vphantom{\Bigl(}}$

これで、未知数を解く直線の明示的な方程式を決定できるようになりました。

$y$

暗黙的な方程式:

$4x-2y-14=0$

$-2y=-4x+14$

$y=\cfrac{-4x+14}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=2x-7}\quad \vphantom{\Bigl(}}$

したがって、直線の傾きは 2 (独立変数に付随する項) に等しくなります。

$x$

）。

$m=2$

これにより、直線の点と傾きの方程式を次の式で計算できます。

$y-P_2=m(x-P_1)$

$y-(-1)=2(x-3)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y+1=2(x-3)}\quad \vphantom{\Bigl(}}$

最後に、線の部分方程式を見つけるために、軸 OX および OY との交点を計算し、その式を適用します。

$y=2x-7$

横軸（X軸）との交点

$y=0$

$0=2x-7$

$-2x=-7$

$x=\cfrac{-7}{-2} = \cfrac{7}{2}$

$\displaystyle \left(\frac{7}{2}, 0\right)$

y軸との交点(Y軸)

$x=0$

$y=2\cdot 0-7$

$y=-7$

$\displaystyle \left(0,-7\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\frac{\bm{7}}{\bm{2}}}+\cfrac{\bm{y}}{\bm{-7}} \bm{= 1} \quad \vphantom{\Biggl(}}$

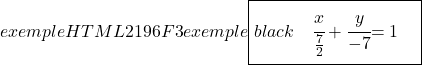
2点を通る直線方程式

直線方程式におけるもう 1 つの非常に一般的な問題は、指定された 2 つの点によって決定される直線の方程式を見つけることです。 2 つの点を使用して直線の方向ベクトルを計算し、方程式を計算することもできますが、以下では、直線の方程式を直接かつ簡単に求めることができる公式を提供します。

直線上にある 2 つの点を考えてみましょう。

$P_1(x_1,y_1) \qquad \qquad P_2(x_2,y_2)$

2 点から直線の方程式を求める公式は次のとおりです。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1) \end{empheq}$

この公式を使用すると、直線が通過する 2 つの点が与えられた場合に、直線の点と傾きの方程式を直接計算できます。

直線の方程式の問題を解決しました

演習 1

点によって定義される直線のベクトル方程式、パラメトリック方程式、連続方程式を求めます。

$P$

そしてその方向性のベクトル

$\vv{\text{v}}.$

両方である:

$P(0,3) \qquad \qquad \vv{\text{v}}=(-1,5)$

解決策を参照

まず、式から直線のベクトル方程式を計算します。

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(0,3)+t\cdot (-1,5)} \quad \vphantom{\Bigl(}}$

次に、対応する式を使用して、線のパラメトリック方程式を見つけます。

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

そして最後に、それぞれの式を使用して直線の連続方程式を決定します。

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-0}{-1}=\cfrac{y-3}{5}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x}}{\bm{-1}}\bm{=}\cfrac{\bm{y-3}}{\bm{5}}\quad \vphantom{\Biggl(}}$

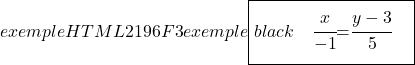
演習 2

点によって決定される直線の陰的な方程式、陽的な方程式、および点と傾きの方程式を求めます。

$P$

そしてその方向ベクトルは

$\vv{\text{v}}.$

$P(-4,3) \qquad \qquad \vv{\text{v}}=(2,6)$

解決策を参照

直線の暗黙的な方程式の式は次のとおりです。

$Ax+By+C=0$

したがって、係数 A、B、C を見つける必要があります。次の等式が常に検証されるため、未知数 A と B は直線の方向ベクトルの座標から取得されます。

$\vv{\text{v}}= (-B,A)$

したがって、係数 A はベクトルの 2 番目の座標であり、係数 B は符号が変更されたベクトルの最初の座標です。

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}$

したがって、係数 C を見つけるだけで済みます。これを行うには、直線に属することがわかっている点をその方程式に代入する必要があります。

$P(-4,3)$

$6x-2y+C=0 \ \xrightarrow{x=-4 \ ; \ y=3} \ 6\cdot (-4)-2\cdot 3+C=0$

$-24-6+C=0$

$-30+C=0$

$C=30$

したがって、この直線の暗黙的な一般方程式またはデカルト方程式は次のようになります。

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x-2y+30=0}\quad \vphantom{\Bigl(}}$

これで、未知数を解く直線の明示的な方程式を決定できるようになりました。

$y$

暗黙的な方程式:

$6x-2y+30=0$

$-2y=-6x-30$

$y=\cfrac{-6x-30}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=3x+15}\quad \vphantom{\Bigl(}}$

したがって、直線の傾きは 3 (独立変数の前の項) に等しくなります。

$x$

）。

$m=3$

そして、線の傾きの値から、次の式で線の点と傾きの方程式を計算できます。

$y-P_2=m(x-P_1)$

$y-3=3(x-(-4))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-3=3(x+4)}\quad \vphantom{\Bigl(}}$

演習 3

陰的な方程式または一般方程式として表される、次の直線上の 3 つの点を決定します。

$4x+2y-8 = 0$

解決策を参照

直線上の点を計算するには、変数の 1 つに値を代入し、その点でのもう 1 つの変数の値を見つけるだけです。

次のようにして最初の点を計算します

$x=0:$

$4\cdot 0+2y-8 = 0$

$2y = 8$

$y = \cfrac{8}{2}$

$y = 4$

$\bm{P_1(0,4)}$

次に、変数に別の値を与える 2 番目の点を見つけます。

$x,$

例えば

$x=1:$

$4\cdot 1+2y-8 = 0$

$2y = 8-4$

$2y = 4$

$y = \cfrac{4}{2}$

$y = 2$

$\bm{P_2(1,2)}$

そして最後に、次のことを解いて 3 番目の点を計算します。

$x=2:$

$4\cdot 2+2y-8 = 0$

$2y = 8-8$

$2y = 0$

$y = \cfrac{0}{2}$

$y = 0$

$\bm{P_3(2,0)}$

演習 4

点によって定義される直線のすべての方程式を検索します

$P$

そしてベクトル

$\vv{\text{v}}.$

$P(-1,4) \qquad \qquad \vv{\text{v}}=(-3,6)$

解決策を参照

まず第一に、その公式から直線のベクトル方程式を見つけます。

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(-1,4)+t\cdot (-3,6)} \quad \vphantom{\Bigl(}}$

次に、対応する式を通じて線のパラメトリック方程式を見つけます。

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

また、その公式を使用して直線の連続方程式も決定します。

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{-3}=\cfrac{y-4}{6}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x+1}}{\bm{-3}}\bm{=}\cfrac{\bm{y-4}}{\bm{6}}\quad \vphantom{\Biggl(}}$

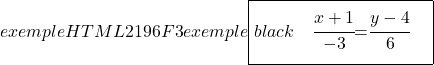
次に、直線の陰的方程式または一般方程式を求める作業に移りましょう。これを行うには、連続方程式の 2 つの部分を交差させます。

$6\cdot (x+1)= -3 \cdot (y-4)$

$6x+6= -3y+12$

$6x+6+3y-12=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x+3y-6=0}\quad \vphantom{\Bigl(}}$

これで、未知数を解く直線の明示的な方程式を決定できるようになりました。

$y$

暗黙的な方程式:

$6x+3y-6=0$

$3y=-6x+6$

$y=\cfrac{-6x+6}{3}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=-2x+2}\quad \vphantom{\Bigl(}}$

したがって、直線の傾きは -2 (独立変数に伴う項) に相当します。

$x$

）。

$m=-2$

これにより、直線の点と傾きの方程式を次の式で計算できます。

$y-P_2=m(x-P_1)$

$y-4=-2(x-(-1))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-4=-2(x+1)}\quad \vphantom{\Bigl(}}$

最後に、線の部分方程式を見つけるために、線と軸 OX および OY の交点を計算し、その式を使用します。

$y=-2x+2$

横軸（X軸）との交点

$y=0$

$0=-2x+2$

$2x=2$

$x=\cfrac{2}{2} =1$

$\displaystyle \left(1, 0\right)$

y軸との交点(Y軸)

$x=0$

$y=-2\cdot 0+2$

$y=2$

$\displaystyle \left(0,2\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\bm{1}}+\cfrac{\bm{y}}{\bm{2}} \bm{= 1} \quad \vphantom{\Biggl(}}$

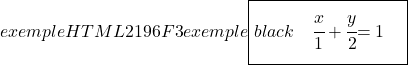
演習 5

次の 2 点を通る直線の方程式を求めます。

$P_1 (4,-1) \qquad \qquad P_2(5,2)$

解決策を参照

直線上の 2 つの点がすでにわかっているので、直線の方程式の公式を指定された 2 つの点に直接適用します。

$y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1)$

次に、点のデカルト座標を式に代入します。

$y-(-1)= \cfrac{2-(-1)}{5-4} (x-4)$

そして最後に、線の傾きを計算します。

$y+1= \cfrac{3}{1} (x-4)$

$y+1= 3(x-4)$

したがって、これら 2 点を通る直線の方程式は次のようになります。

$\bm{y+1= 3(x-4)}$

直線の方程式はすべて何ですか?

直線のベクトル方程式

直線のパラメトリック方程式

連続直線方程式

暗黙的または一般的な直線の方程式

明示的な直線の方程式

パラメータ m と n の意味

線の傾きを計算する

直線の点と傾きの方程式

直線の正準方程式または部分方程式

すべての直線の方程式（公式）

直線の方程式の計算例

2点を通る直線方程式

直線の方程式の問題を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

コメントする返信をキャンセル