別の点、線、平面に対して対称な点

ここでは、別の点、線、平面に対する対称点を計算する方法を説明します。さらに、例題や演習を段階的に解くことができます。

別の点に対して対称な点

対称点がどのように計算されるかを説明する前に、別の点に関して対称点とは正確には何なのかを確認してみましょう。

点 A’ が点 M から点 A と点 M の間の距離と同じ距離に対称的に位置する場合、点 A’ は別の点 M に関して点 A の対称点です。したがって、M は次の式で形成される線分の中点です。点AとA’。

$d(A,M) = d(A',M )$

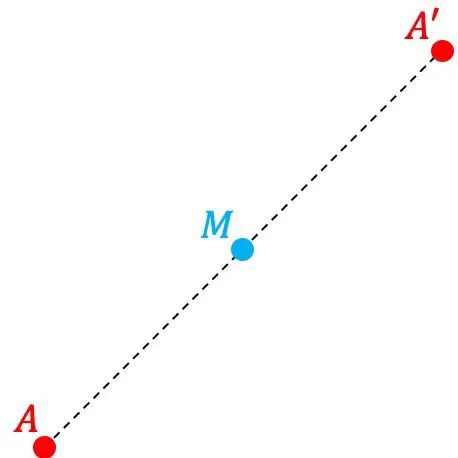
一方で、点 M が対称の中心であるとも言います。

したがって、対称点の座標を計算するには、セグメントの中点の公式を使用します。

$\cfrac{A+A'}{2}=M$

この方程式から未知の点 A’ を抽出し、別の点に関して対称な点の公式を取得します。

$\color{orange} \boxed{ \color{black} \quad A' = 2M - A \quad \vphantom{\Bigl)}}$

他の点に対して対称な点を求める例

例として、点 M に対する点 A の対称点を計算します。次の 2 つの点を考慮します。

$A(1,3,0) \qquad \qquad M(-1,4,2)$

これら 2 つの点間の対称点を決定するには、別の点に関する対称点の公式を適用します。

$A' = 2M - A$

ここで、式内の点を置き換えます。

$A' = 2(-1,4,2) -(1,3,0)$

そして私たちは以下のことを行っています。

$A' = (-2,8,4) -(1,3,0)$

$\bm{A'=(-3,5,4)}$

直線に対して対称な点

別の点に関して対称な点の概念を見てきました。さて、線に対する点の対称点は非常によく似ています。

点A’は、2つの点A’とAが直線に垂直な同一直線上にあり、さらに、点A’と直線の間の距離が距離に等しい場合、点Aの線対称な点です。点Aと直線の間。

$d(A,r)= d(A',r)$

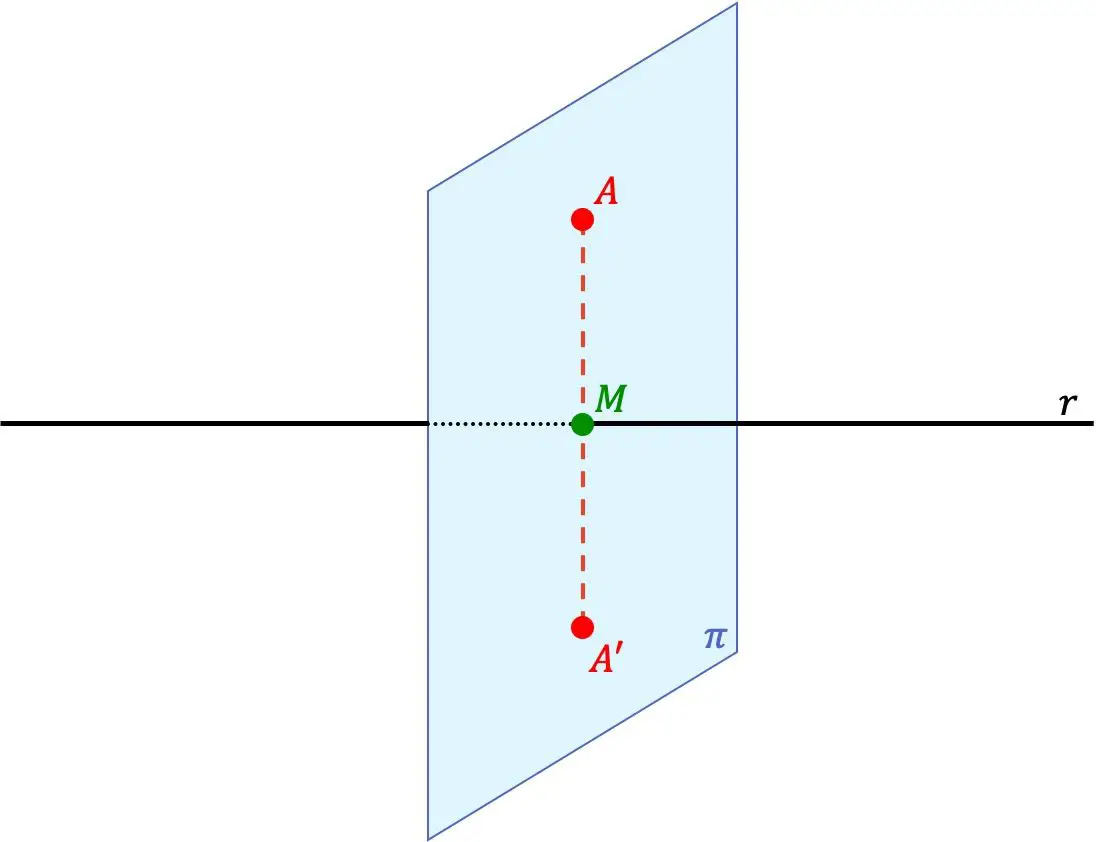
したがって、線r は点間の対称軸でもあります。

したがって、線rに対する点 A の対称点を決定するには、次の手順に従う必要があります。

点 A を通過する線rに垂直な平面 (前のグラフィック表現の平面 π) を見つけます。これを行うには、平面の法線ベクトルとなる線の方向ベクトルを使用する必要があります。
見つかった平面と直線との交点(前の画像の点 M) を計算します。
点に関する対称点の式 (上のセクションで参照) を使用して、点 M に対する点 A の対称点を見つけます。結果は、探していた対称点です。

線対称点の計算例

線に対する別の点の対称点を計算する方法がわかったら、例として演習を解いていきます。

直線rに関して点Aの対称点を求めます。点と線でこう言われます。

$\displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}$

まず、点 A を通る直線 r に垂直な平面を計算する必要があります。この平面に垂直なベクトルが直線の方向ベクトルとなり、その成分がパラメーターの前の項になります。

$t$

それはパラメトリック方程式の形式で表現されるためです。

$\vv{n}=(1,4,-3)$

そして、平面の方程式の係数 A、B、C はその法線ベクトルの座標と一致するため、次のようになります。

$\vv{n}=(1,4,-3) \quad \longrightarrow \quad \pi : \ 1x+4y-3z+D=0$

点 A はこの平面上にある必要があるため、点 A を平面の方程式に代入して係数 D を求めることができます。

$A(4,0,-1)$

$4+4\cdot 0-3\cdot (-1)+D=0$

$4+3+D=0$

$7+D=0$

$D=-7$

したがって、点 A を通る直線 ry に垂直な平面の方程式は次のようになります。

$\pi : \ x+4y-3z-7=0$

平面の方程式がわかったら、平面と直線の交点を計算する必要があります。これを行うには、線の座標を平面の方程式に代入し、結果として得られる方程式を解きます。

$\displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0$

$(1+t)+4(5+4t)-3(-4-3t)-7=0$

$1+t+20+16t+12+9t-7=0$

$26t+26=0$

$26t=-26$

$t=\cfrac{-26}{26}$

$t=-1$

ここで、次の値を置き換えます。

$t$

次の直線の方程式で得られます。

$\displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}$

したがって、線 r とそれに垂直な平面との交点は次のようになります。

$M(0,1,-1)$

最後に、点 M に関して点 A の対称点を見つけるだけで十分です。このためには、このページの冒頭にある式を使用できます。

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}$

平面に対して対称な点

平面に対する別の点の対称点を決定する方法を説明する前に、その定義が何であるかを見てみましょう。

点A’は、2つの点A’とAが平面に垂直な同一線上にあり、かつ、点A’と平面の間の距離が距離に等しい場合、点Aの対称点です。点Aと平面の間。

$d(A,\pi)= d(A',\pi)$

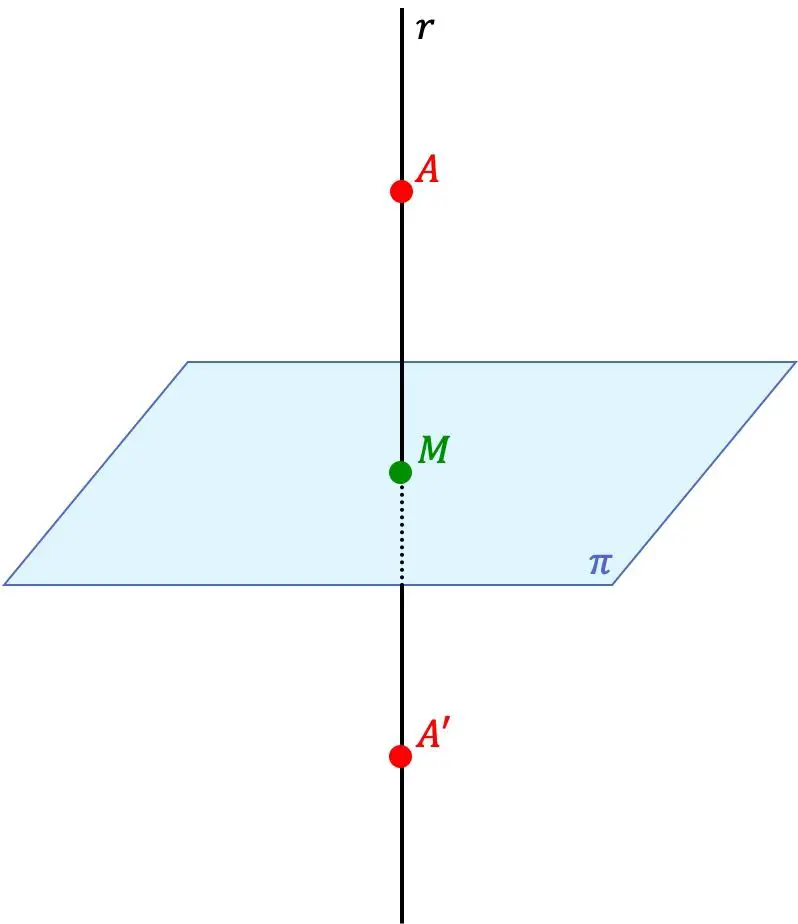
したがって、この平面は 2 点間の対称面でもあります。

したがって、平面 π に関して点 A の対称点のデカルト座標を知るには、次の手順に従う必要があります。

点 A を通る平面に垂直な線の方程式を求めます。このために、平面に垂直なベクトルを線の方向ベクトルとして使用します。
平面と見つかった線との交点 (前の画像の点 M) を計算します。
点に関する対称点の式 (最初のセクションで示した) を使用して、点 M に対する点 A の対称点を見つけます。結果は、探していた対称点です。

平面に対する対称点の決定例

以下に、平面に対する別の点の対称点に関する解決済みの問題を示します。

平面 π に対する A の対称点を決定します。要点と計画を述べた上で、次のようにします。

$\displaystyle A(3,-4,2) \qquad \qquad \pi: \ 2x+y-z-6=0$

最初に行う必要があるのは、点 A を通る平面に垂直な線の方程式を見つけることです。これを行うには、平面に垂直なベクトルを線の方向ベクトルとして使用できます。その成分 X、 Y、Z はそれぞれ、平面の方程式の項 A、B、および C の係数です。

$\pi: \ 2x+y-z-6=0 \quad \longrightarrow \quad \vv{n} = (2,1,-1)$

これで、見つかった方向ベクトルとその点 (点 A) の 1 つを使用して、平面に直交する直線のパラメトリック方程式を構築できます。

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases}$

垂線がわかったら、直線の座標を平面の方程式に代入して、平面と直線の交点を計算します。

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases} \qquad \qquad \pi : \ 2x+y-z-6=0$

$2(3+2t)+(-4+t)-(2-t)-6=0$

$6+4t-4+t-2+t-6=0$

$6t-6=0$

$6t=6$

$t=\cfrac{6}{6}$

$t=1$

ここで、次の値を置き換えます。

$t$

次の直線の方程式で得られます。

$\displaystyle t=1 \ \longrightarrow \ \begin{cases}x=3 + 2\cdot 1 =5\\[1.7ex] y=-4 +1=-3\\[1.7ex] z=2-1=1 \end{cases}$

したがって、平面と垂線の交点は次のようになります。

$M(5,-3,1)$

最後に、点 M に関して点 A の対称点を見つける必要があります。これを行うには、このページの冒頭にある公式を使用できます。

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(5,-3,1) - (3,-4,2) \\[2ex] & = (10,-6,2)-(3,-4,2)\\[2ex] & = \bm{(7,-2,0)} \end{aligned}$

他の点、線、面に対して対称な点

別の点に対して対称な点

他の点に対して対称な点を求める例

直線に対して対称な点

線対称点の計算例

平面に対して対称な点

平面に対する対称点の決定例

コメントする返信をキャンセル

別の点に対して対称な点

他の点に対して対称な点を求める例

直線に対して対称な点

線対称点の計算例

平面に対して対称な点

平面に対する対称点の決定例

コメントする 返信をキャンセル

コメントする返信をキャンセル