直交行列 - マソリティ

このページでは、直交行列とは何か、および直交行列と逆行列との関係について説明します。また、それを完全に理解するためにいくつかの例も表示されます。さらに、直交行列をチェックする公式も教えます。これを使用すると、直交行列をすばやく見つける方法がわかります。最後に、これらの特定の行列の特性と応用、および典型的な解答済みの試験演習が見つかります。

直交行列とは何ですか?

直交行列の定義は次のとおりです。

直交行列は、転置（または転置）を乗じた正方実数行列であり、単位行列と等しくなります。つまり、次の条件が満たされます。

$A\cdot A^t = A^t \cdot A =I$

金

$A$

は直交行列であり、

$A^t$

はその転置行列を表します。

この条件を満たすには、直交行列の列と行が直交単位ベクトルである必要があります。つまり、正規直交基底を形成している必要があります。このため、一部の数学者はこれらを正規直交行列と呼ぶこともあります。

直交行列の逆行列

直交行列の概念を説明するもう 1 つの方法は、直交行列の転置 (または転置) 行列がその逆行列に等しいため、逆行列を使用することです。

この定理を完全に理解するには、逆行列の方法を知っておくことが重要です。このリンクでは、逆行列とそのすべてのプロパティの詳細な説明が見つかり、さらにステップごとに解決された練習問題も提供されます。

直交行列の逆行列は、直交行列条件と逆行列の主な特性を使用して、その転置と同等であることを簡単に示すことができます。

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

したがって、直交行列は常に可逆行列、つまり、正規行列または非縮退行列になります。

次に、直交行列の例をいくつか見て、すべての概念を理解します。

2×2直交行列の例

次の行列は 2×2 次元の直交行列です。

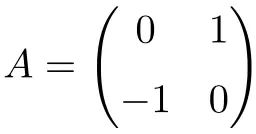
転置による積を計算することで、直交であることを確認できます。

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

結果は同一行列となるため、A が直交行列であることを確認します。

3×3直交行列の例

次の行列は 3×3 次元の直交行列です。

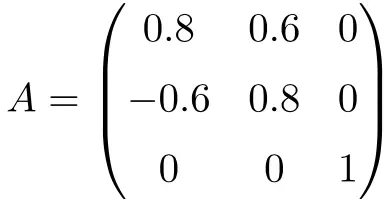
行列 A にその転置を乗算することで、それが直交であることを示すことができます。

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

解はユニタリ行列であるため、A が直交行列であることを示します。

2×2直交行列を求める公式

次に、次数 2 のすべての直交行列が同じパターンに従うという証明を見ていきます。

サイズ 2×2 の一般的な行列を考えてみましょう。

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

この行列が直交するには、次の行列方程式が満たされる必要があります。

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

行列の乗算を解くと、次の方程式が得られます。

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

よく見ると、これらの等式は基本的なピタゴラス三角関係によく似ています。

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

その結果、式 (1) および (3) を満たす項が得られます。

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

さらに、2 番目の方程式に値を代入すると、2 つの角度の関係が得られます。

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

つまり、次の 2 つの条件のいずれかを満たす必要があります。

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

したがって、結論として、直交行列は次の 2 つの行列のいずれかの構造を持つ必要があります。

金

$\theta$

は実数です。

実際、例として値を付与すると、

$\displaystyle\theta=\frac{\pi}{2}$

最初の構造を取得すると、「2×2 直交行列の例」セクションで直交であることが確認された行列が得られます。

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

直交行列のプロパティ

このタイプのマトリックスの特徴は次のとおりです。

直交行列は常に反転できるため、特異行列になることはありません。この意味で、直交行列の逆行列は別の直交行列です。

任意の直交行列は対角化できます。したがって、直交行列は直交対角化可能であると言います。

すべての固有値、または直交行列の固有値は、1 に等しい係数を持ちます。

実数のみで構成される直交行列も正規行列です。

複素数環境における直交行列の類似物は、ユニタリ行列です。

明らかに、単位行列は直交行列です。

n × n 次元の直交行列の集合と行列の積の演算は、直交群と呼ばれる群を形成します。つまり、2 つの直交行列の積は、別の直交行列と等しくなります。

さらに、直交行列に転置を乗算した結果は、クロネッカーデルタで表すことができます。

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

最後に、直交行列の行列式は常に +1 または -1 です。

$\displaystyle \text{det}(A)=\pm 1$

直交行列の解決済み演習

次に、直交行列の練習問題を解きます。

次の次数 3 の正方行列が与えられた場合、次の値を求めます。
$a$

そして

$b$

直交させるには:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

行列の直交性が満たされるためには、行列の転置による積が恒等行列に等しくなければなりません。それで：

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

行列を乗算します。

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$