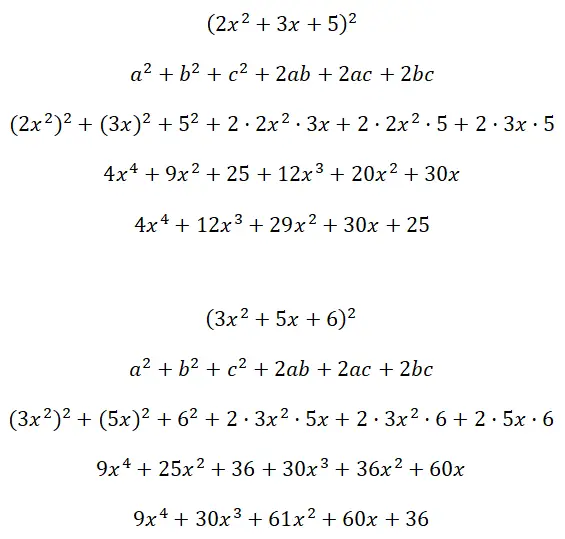注目すべき製品や注目すべきアイデンティティとは何ですか?
顕著な恒等式 は、顕著な積または顕著な等式とも呼ばれ、多項式の積と商をより迅速に解くことを可能にする数学的リソースです。恒等という言葉が示すように、これらは、これらの演算を解くことなく計算できるようにする等式です。この式は固定ルール (常に満たされる) に従っていることがわかっているため、チェックすることなく結果を取得できます。
注目に値するアイデンティティをいつ使用するか?
これらの恒等式は主に代数学の分野で使用され、その主な機能は、演算自体をすべて解く必要なく、特定の多項式の解を高速化することです。そこから注目すべき製品の配合を取得し、それについて記事全体で解説します。そして最後に、完全平方、因数多項式、またはその他のタイプの計算に数式を適用できます。
注目すべき製品を段階的に解決するにはどうすればよいでしょうか?
重要な ID を解決するには、非常に簡単な手順に従う必要がありますが、これも非常に理にかなっています。
- 注目すべきアイデンティティのタイプを特定する:最初のステップは、操作のタイプ (注目すべき製品または注目すべき商材) を特定することです。また、どのようなタイプの式を適用する必要があるのかを明確にする必要があります。これについては、注目すべきアイデンティティのさまざまなタイプを説明した後で理解します。
- 式を適用する:適用する必要がある式がわかったら、計算を実行します。 ID のタイプに応じて、多かれ少なかれ複雑な演算を解決する必要があり、ほとんどの場合、これらの計算は少なくとも 1 つの未知の項を含む項で構成されます。
- 式を簡略化する:最後に、結果を取得したら、それを簡略化する必要があります。このステップでは、類似した項をグループ化し、それらを順序付けして、適切に構造化された多項式を形成する必要があります。このステップは他のステップと同様に重要であることに注意してください。そうしないと演習が不完全なままになるためです。
注目すべきアイデンティティまたは主要な注目すべき製品の公式
以下に、注目すべきアイデンティティに対応するすべての式を示します。各ケースの理論的な説明に加えて、解決済みの注目すべき製品例もいくつかあり、それを通じてすべての概念をより深く理解できます。この最初のセクションでは、最も重要なアイデンティティのみを説明することに注意してください。しかし、この記事を読むことで、三項式で作られた製品など、より複雑で注目すべき製品を開発する方法を学ぶことができます。
和の二乗
最初のケースは、和の 2 乗に関するもので、代数学の世界で非常に一般的な多項式です。これは (a + b) 2と書くことができ、これは (a + b) · (a + b) と同等です。したがって、多項式乗算を使用して解決できることがわかります。しかし、注目に値するアイデンティティのおかげで、次の式を使用することで時間を節約できます: (a + b) 2 = a 2 + 2ab + b 2 。次に、今見た公式のデモンストレーションを示します。これにより、それがどこから来てどのように使用されるかを理解できるようになります。
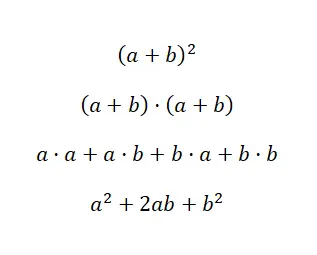
ご覧のとおり、以前にコメントした多項式の乗算を使用して検証を実行しました。そして、結果の式を暗記していれば、単純な値の置換を実行するだけで、より速く結果を得ることができると絶対の確信を持って言えます。したがって、これは非常に有用な数学的概念です。和の二乗がどのように機能するかがわかったので、具体的な例を示します。
和の二乗の例
注目すべき恒等式 (2x + 4) 2を計算します。
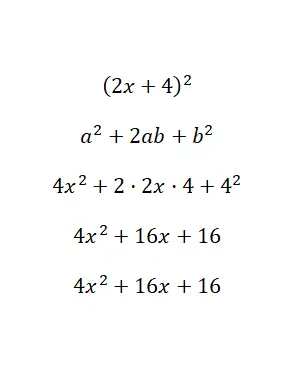
基本的に、二項式の値を式の文字に関連付けて、a = 2x および b = 4 を解きました。最後に、すべての計算を解いた後、多項式 4x 2 + 16x + 16 が得られます。これは次のとおりです。オリジナルと同等。この例では、縮小多項式から拡張多項式 (標準形式) を取得しました。
減算の二乗
もう 1 つの非常に一般的な表現は、減算の 2 乗です。これは加算の 2 乗によく似ており、符号が 1 つ変わるだけです。この場合、二項式の構造は (a – b) 2と等価であり、これを展開すると、(a – b) · (a – b) が得られます。前のケースと同様、これは多項式の乗算から計算できますが、解を容易にする公式 a 2 – 2ab +b 2もあります。以下にこれの経験的証明を示します。
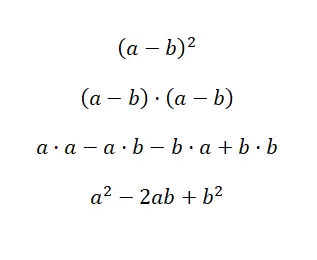
差の 2 乗の計算を簡素化するには、2 乗和の計算に使用したのと同じ式を使用できますが、最初の符号が負になります。この最小限の変更により、式を正の項と負の項で構成される二項式に適合させることができ、減算に役立ちます。解決された例を次に示します。
減算の二乗の例
注目すべき恒等式 (x – 3) 2を計算します。
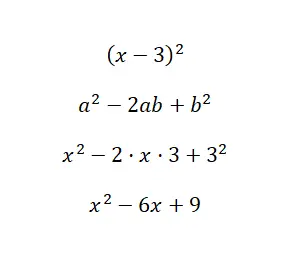
ソリューション例でわかるように、二項式の値を式 a = x および b = 3 に代入しました。 したがって、前に説明した式を使用すると、置換といくつかの非常に基本的な処理を実行するだけで済みます。計算。これにより、この式を使用して差の 2 乗をいかに簡単に計算できるかがわかります。
二乗の差または差による合計
注目すべき積の 3 番目のケースは二乗の差と呼ばれ、これは正の二項式と負の二項式の積によって形成されます。このスタイルの式は (a + b) · (a – b) という構造を持つため、この積を展開すると、計算を容易にする公式 a 2 – b 2が得られます。ご覧のとおり、これは非常に単純な式ですが、完全に理解するにはすべての計算を作成する必要があります。
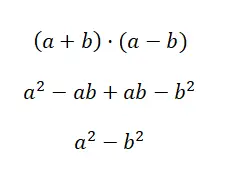
差による合計の例
注目すべき恒等式 (x + 1) · (x – 4) を計算します。
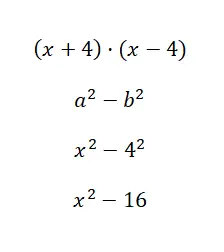
このときの数値計算は非常に簡単で、実際にはべき乗を解くだけで済みます。確かにこの公式は、二項式が同じ主項と同じ独立項を持ち、符号が変更されている場合にのみ適用できます。したがって、この ID は重要ですが、最も頻繁に使用するものではありません。
共通項を持つ 2 つの二項式の積
この 4 番目のケースでは、構造がわずかに変更されていますが、前のケースと非常によく似た状況に直面していることがわかります。 (x + a) · (x + b) と (a + b) · (a – b) の違いを観察してください。まだよくわからない場合は、(x + 4) · (x + 5) および (x + 4) · (x – 4) の例を考えてください。最初のケース ( 2 つの共通項 binomials の積) では共有項が 1 つだけありますが、2 番目のケース (差分による合計) では 2 つの項は共通ですが、独立項の符号が反転しています。そうは言っても、どのような式で動作できるかを見てみましょう。
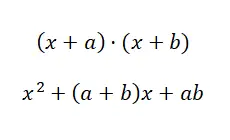
共通項を持つ 2 つの二項式の積の例
注目すべき積 (x + 2) · (x + 3) を解きます。
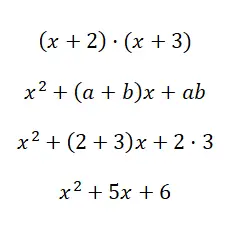
x 2 + (a + b)x + ab の公式を使用すると、2 つの二項式の乗算から得られる 2 次多項式を計算できます。場合によっては区別するのが難しい場合があるため、この例を通じて、説明した最後の 2 つのケースの違いを理解していただければ幸いです。
三項の二乗
三項式の二乗を計算しようとすると、作業を楽にしてくれる素晴らしい製品もあります。この式は、(a + b + c) 2のように表され、等価な積は、a 2 + b 2 + c 2 + 2ab + 2ac + 2bc となります。これは正の三項式の場合には有効ですが、係数の 1 つが負の場合は、式に負の値を書き込むだけでよいことに注意してください。以下は式のデモンストレーションです。
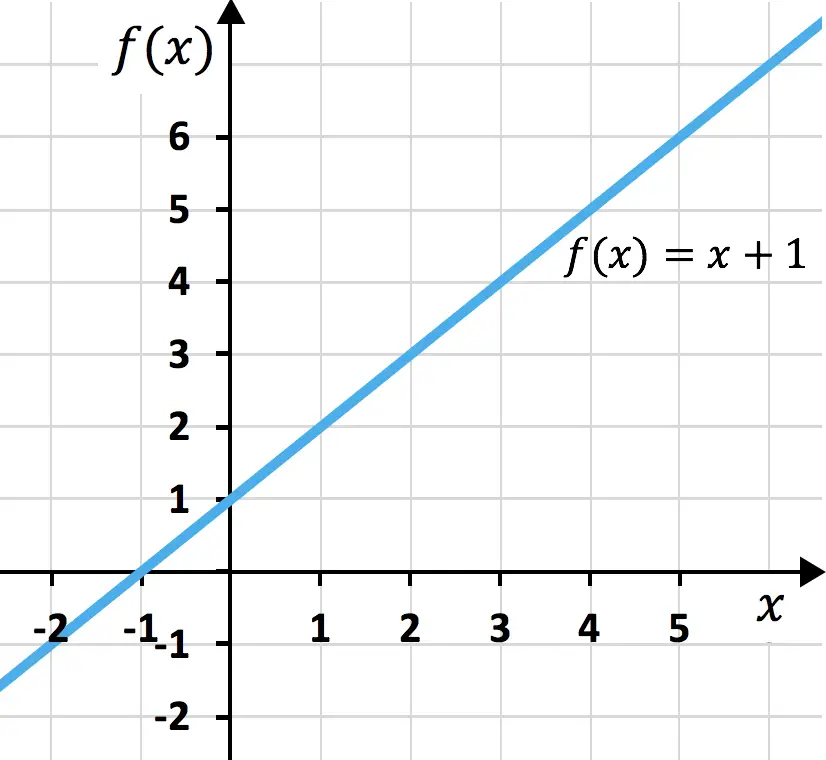
三項式の二乗の例
注目すべき恒等式 (2x + 1 + x 2 ) 2を計算します。
注目に値するアイデンティティ公式または注目に値する立方体積
主な注目すべき恒等式について説明したので、二項式の 3 乗から始めて、それらの導関数を見ていきます。このスタイルの注目すべき製品を計算するには、もう少し複雑ですが、すでに説明したものと同様の構造に従う式に頼る必要があります。
二項三乗
二項式の 3 乗は(a + b) 3および (a – b) 3と書きます。この式は次の式と同等です: (a 3 + 3a 2 b + 3ab 2 + b 3 )、および (a 3) – 3a 2 b + 3ab 2 – b 3 )。これら 2 つの場合は、二項の 3 乗であるため、和の 3 乗および減算の 3 乗と呼ばれます。以下に、各ケースの非常に詳細なデモを示します。
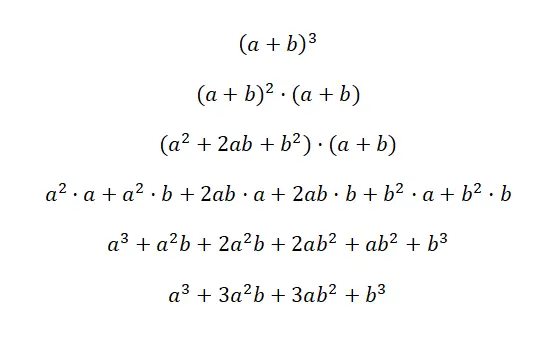
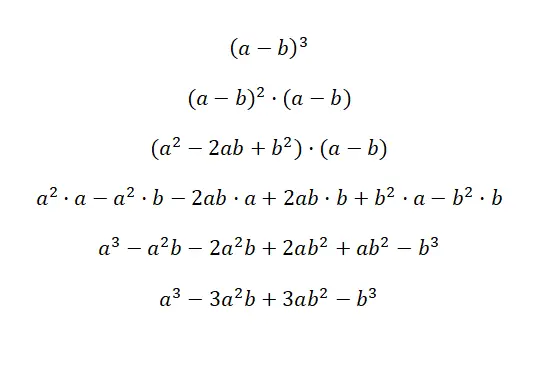
この最初の証明を理解する鍵は、(a + b) 3が (a + b) 2 · (a + b) と同等であることを理解することです。このようにして、他の係数を乗算するために以前に説明した sum の 2 乗の公式を使用します。次に、式を単純化して、対応する注目すべき恒等式 a 3 + 3a 2 b + 3ab 2 + b 3を取得します。 2 番目の例の場合も、符号が変わりますが、同じことが起こります。
二項立方体の例
注目すべき恒等式 (x + 3) 3を解く :
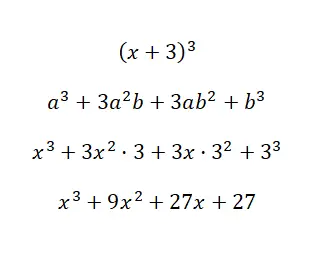
先ほど説明した公式を使用すると、a = xyb = 3 を考慮して多項式を計算できます。ご覧のとおり、手順は非常に単純で、計算に多くの複雑さはありません。これは、次の公式があるためです。 。そうしないと、これほど多くの乗算を行うのは非常に面倒になります。
3乗の和と3乗の差
前のケースと混同されやすい別のケースもあります。 2 つのケースは書き方が異なりますが、同等ではありません。立方体の和または差に相当する式は a 3 + b 3ですが、前のケースでは (a + b) 3について説明しました。ご覧のとおり、式の構造には紛れもない類似点がありますが、実際には、計算の開発となると、これらは 2 つのまったく異なるケースになります。
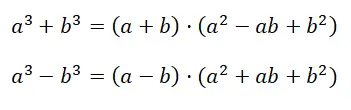
式のデモンストレーションでは、最初の多項式の因数分解を取得します。正確には、最初の二項式から二項式と三項式の積に進みます。得られた結果 (a + b) · (a 2 – ab + b 2 ) はまったく計算を単純化していないように見えますが、実際には、多項式を因数分解すると、非常に理解しやすい式が得られます。
3乗和の例
注目すべき積 x 3 + 27 を計算します。
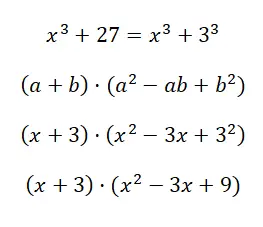
この場合、これ以上単純化できないため、得られる結果は非常に長くなります。しかし、この式に到達するのは通常のことであり、実際、このような場合には、この例のように、二項式と三項式の積に相当する構造の結果しか得られません。
三項三乗
三項式の 3 乗は(a + b + c) 3と書きます。これは、3 つの同一の三項式を乗算することになりますが、指数は付きません: (a + b + c) · (a + b + c) · (a + b +c)。これは、存在する積の中で最も複雑で注目すべき積ですが、式は非常に論理的であり、対応する多項式の乗算を実行すると、他の積と同じ方法で得られます。以下に、この注目すべきアイデンティティの公式の証明を示します。
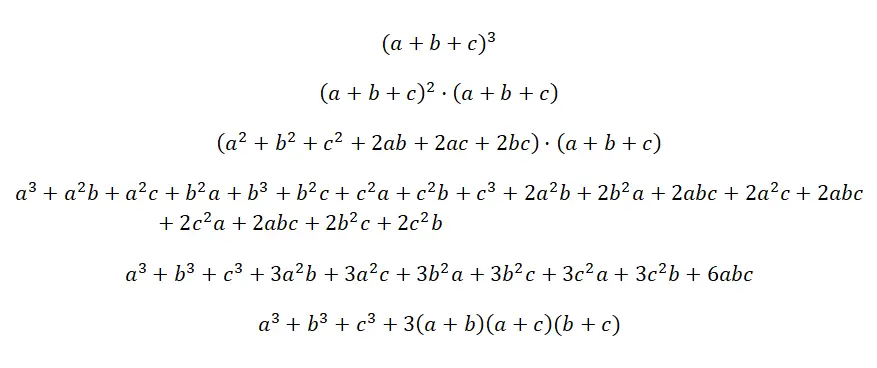
三項式の立方体の例
次の三項立方体 (x 2 + 3x – 4) 3を解きます。
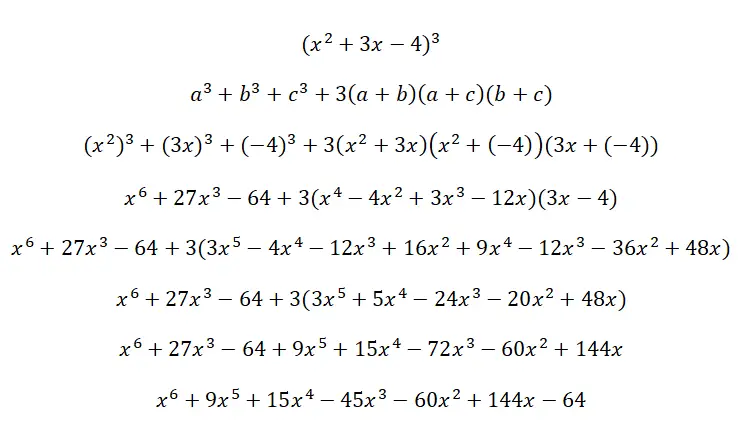
顕著な比率
最後に、特定の種類の代数分数をすばやく解くための注目すべき恒等式である注目すべき商について説明します。より正確には、4 つの異なるタイプがあり、1 つの特性を共有しています。それは、その結果が正確な多項式 (剰余が 0 に等しい) で構成されているということです。また、注目すべき商の公式は、すでに説明した注目すべき積の公式と一定の関係があることにも言及する価値があります。
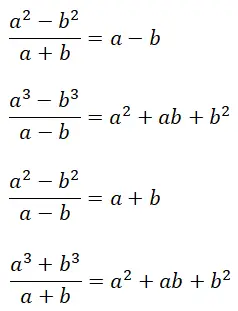
顕著な比率が解決された例
次の注目すべき比率を計算します。
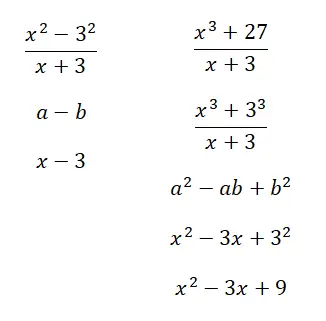
注目すべき製品に関する演習が解決されました
さまざまな注目点がどのように解決されるかがわかったので、少し練習してみましょう。これが、説明したすべての理論を適用するための6 つの演習を提供する理由です。また、すべての演習を解くときに手元に置いておけるように、主要な注目すべきアイデンティティの表を示します。

演習 1
二項平方 (x – 4) 2 、(x + 1) 2 、および (x – 3) 2を解きます。
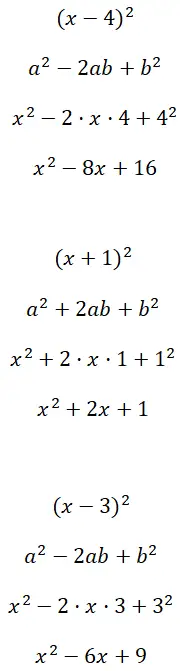
演習 2
2 乗の差 (x – 1) · (x + 1) と (x + 3) · (x – 3) を計算します。
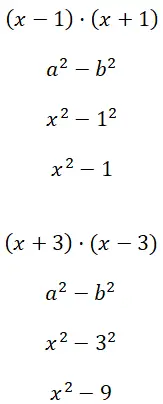
演習 3
注目すべき製品を 3 乗 (x – 5) 3および (x + 8) 3に展開します。
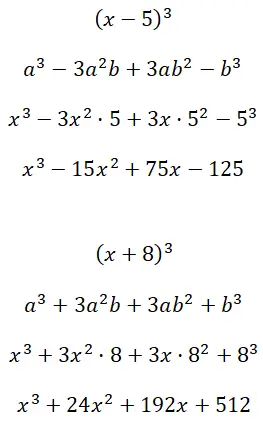
演習 4
多要素項 (4x 2 + 5y) 2 、(5x 3 + y 2 ) · (5x 3 – y 2 ) および (5xy 2 – 2xy) 2から形成される注目すべき恒等式を開発します。
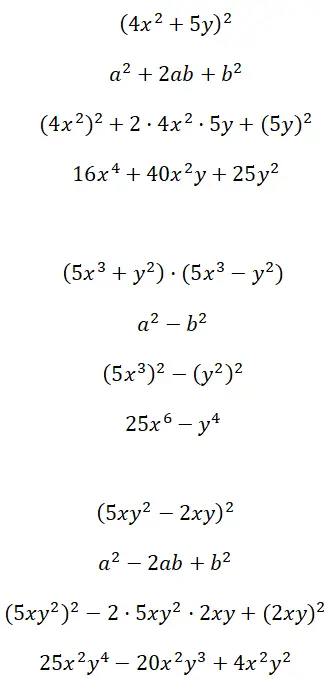
演習 5
多因子項 (3x 2 + y) 3および (5y 3 – 2x 2 ) 3によって形成される注目すべき 3 次積を計算します。
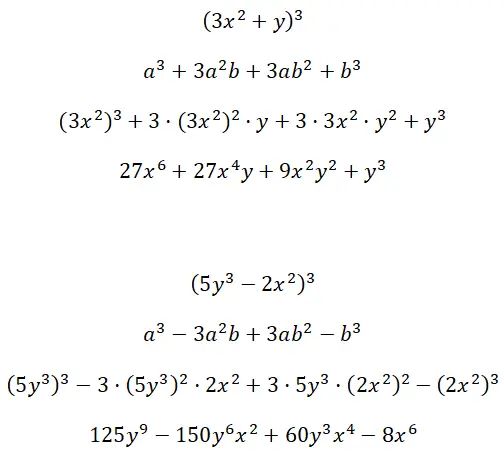
演習 6
三項式 (2x 2 + 3x + 5) 2および (3x 2 + 5x + 6) の 2 乗を解きます。