このページでは、正規行列とは何かと、正規行列の例を示します。さらに、このタイプの行列のプロパティと演習を段階的に解決します。
正規行列とは何ですか?
通常の配列定義は次のとおりです。
ただし、それらが実数行列の場合、前の条件は、行列が転置と可換であることを意味します。つまり、次のようになります。
![]()
なぜなら、明らかに、実数行列の共役転置行列は単に転置(または転置)行列だからです。
正規行列の例
複素数を使用した例
次の次元 2×2 の複素正方行列は正規です。
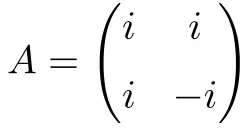
その正常性のデモンストレーションを以下に添付します。
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44b98cec879a8332c462d2393fbfbba_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fddc406493ac1c81c86edf1ad6e58d0b_l3.png)
実数を使った例
次の 2 次の実数を持つ正方行列も正規です。
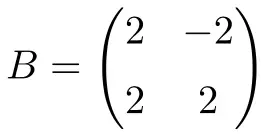
この場合、実数のみを持っているため、それが正規であることを証明するには、行列が転置で可換であることを検証するだけで十分です。
![Rendered by QuickLaTeX.com \displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a320a8e300315c6a48bb8095266408ca_l3.png)
![Rendered by QuickLaTeX.com \displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6ad5bd62deeb5bcbf561a2ee6b29741_l3.png)
正規行列の性質
正規行列には次の特徴があります。
- すべての正規行列は対角化可能な行列です。
- 各ユニタリ行列も正規行列です。
- 同様に、エルミート行列は正規行列です。
- 同様に、反エルミート行列は正規行列です。
- A が正規行列の場合、共役転置行列 A* の固有値 (または固有値) は A の共役固有値です。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91ee46b5f8dda0d51ecb57474f5b816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-48c80a017a9afd8b4cf3923757f4e945_l3.png)
- 通常の行列では、さまざまな固有値に関連付けられた固有ベクトル (または固有ベクトル) は直交します。
- 行列が実数のみで構成され、対称である場合、それは同時に正規行列でもあります。
- 同様に、反対称実行列も正規行列です。
- 最後に、実数で構成される直交行列も正規行列です。
正規行列の演習問題を解決しました
演習 1
次の 2 × 2 次元の複素行列が正規であることを確認します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff27d19373c5a4dc8e95472ec295c657_l3.png)
行列が正規であることを示すには、まず共役転置を計算する必要があります。
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17c96c654ce5b978f90a905b973d5ae7_l3.png)
そして、考えられる両方向で行列 A と行列 A* を乗算して検証を行います。
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36212e1d12cf35ea5dd27bd91d77ee56_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3db0fc8fdc948037452b4c6275896686_l3.png)
両方の乗算の結果は同じであるため、行列 A は正規です。
演習 2
次のサイズ 2 × 2 の実行列が正規行列であることを示します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854e13859be417985691b5ed6d2a050f_l3.png)
この場合、実数のみを含む環境を扱っているため、行列 A とその転置の間の行列積が、乗算の方向に関係なく同じ結果を与えることを検証するだけで十分です。
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1b6314188f394b3053d3dac0613cf5c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2b33f892cd29c0ee232b88eaa4946cc_l3.png)
両方の積の結果は同じであるため、行列 A は正規です。
演習 3
次の 2 次の複素数行列が正規かどうかを判断します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00075db37b045e08349f7d5b3f679570_l3.png)
行列が正規であることを確認するには、まず共役転置を計算する必要があります。
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0b39733376eb2aef269012eb1d6c24be_l3.png)
次に、行列 A とその共役転置が切り替え可能かどうかを確認します。
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c207cb9842dacbaf9bc59d4aaff00473_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bcf52f3da81fd7c56b090604c2b6f368_l3.png)
両方の乗算の結果は同じであるため、行列 A は正規です。
演習 4
次の次元 3×3 の実行列が正規行列であることを確認します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92ee07759c3e6e88af5a68479b5833ea_l3.png)
行列は完全に実数要素で構成されているため、行列 A とその転置の間の行列積が乗算の方向に依存しないことを検証するだけで十分です。
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc7ee02c75239b430c7fc2418f43e343_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e661b877ee225983c797584e2b61d429_l3.png)
両方の積の結果は同じであるため、行列 A は正規です。
演習 5
次の 3×3 次の複素行列が正規かどうかを判断します。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81ca0ac1da07c151a62dcfb06b4be877_l3.png)
まず、行列の共役転置を計算します。
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd0a2dfe1b8bfe18020ab68c1eb3bda6_l3.png)
次に、行列 A とその共役転置の間で行列の乗算を可能な両方の方向で実行する必要があります。ただし、A の共役転置行列は行列 A 自体と等しいため、エルミート行列になります。したがって、正規行列の性質から、すべてのエルミート行列は正規行列であるため、 A は正規行列であることがわかります。