この記事では、直接比例関数とは何か、その公式とは何か、グラフで表現する方法、および特定の点から方程式を計算する方法について説明します。
正比例関数とは何ですか?
正比例関数は、 2 つの正比例する量を関連付ける関数です。したがって、従属変数 (y) の値を計算するには、従属変数 (x) の値に比例定数を乗算する必要があります。
正比例関数は一次関数とも呼ばれます。
一方の量の値が増加すると同時にもう一方の量も増加する場合、およびその逆の場合、2 つの量は正比例することに注意してください。
直接比例関数の計算式
直接比例関数を定義する式は次のとおりです。
![]()
ここで、y は独立変数、x は従属変数、ym は関数の傾きまたは比例定数です。
ご覧のとおり、この式を使用すると、大きさ y の値を計算するのは非常に簡単です。大きさ x の値に、各直接比例関数の特徴である関数の傾きを掛けるだけです。
たとえば、次のような直接比例関数があるとします。
![]()
x が 5 のときに量 y がどのくらいになるかを決定したい場合は、関数 (3) の傾きに 5 を掛けるだけで済みます。
![]()
直接比例関数のグラフ表示
次に、正比例関数をグラフ化する方法を見ていきます。例として次の演習を実行します。
![]()
グラフ上で正比例関数を表すには、座標の原点(点 (0,0)) を通り、関数の傾きを持つ直線を描くだけです。
この場合、表現したい関数の傾きは次のようになります。
![]()
したがって、線は x の単位ごとに y の 2 単位ずつ増加する必要があります。
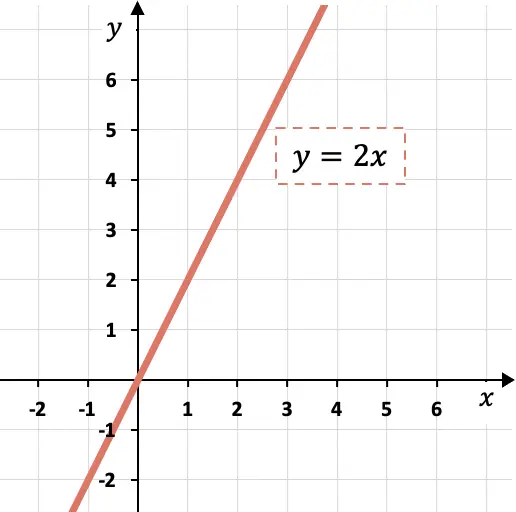
グラフからわかるように、傾きが 2 に等しい場合、y の大きさが x の大きさの 2 倍に増加することを意味します。
直接比例関数はアフィン関数とよく似たグラフを持ちますが、これらは 2 つの異なるタイプの関数です。アフィン関数と線形関数の違いについては、次のリンクで確認できます。
➤参照: 線形関数とアフィン関数の違い
正比例関数の求め方
直接比例関数の点がわかれば、その方程式を簡単に見つけることができます。直接比例関数の問題を解くことでこれがどのように行われるかを見てみましょう。
- 画家が描く部屋の数は、その労働時間にほぼ正比例します。つまり、労働時間が長くなればなるほど、より多くの部屋を描くことができます。彼が 1 日 8 時間で 2 つの部屋全体を塗装したことがわかっている場合、塗装した部屋の数と労働時間を関連付ける正比例関数は何でしょうか?
まず、どれが従属変数でどれが独立変数であるかを判断する必要があります。描かれた作品の数は作業時間に依存し、その逆はありません。したがって、独立変数 (x) は労働時間数、従属変数 (y) は塗装された部屋の数になります。
この問題は、画家が 8 時間で 2 つの部屋をペイントできることを示しているため、関数のグラフは点 (8,2) を通過する必要があります。
![]()
さらに、このステートメントは、2 つの量が直接比例関係にあることを示しています。これは、これらが次の直接比例関数の式に数学的に関連していることを意味します。
![]()
点 (8,2) の座標を方程式に代入することで、関数の傾きの値を計算できます。
![]()
そして最後に、方程式の未知の m を解きます。
![]()
![]()
![]()
つまり、問題の直接比例関数は次のとおりです。
![]()
あなたはおそらくそれも好きでしょう: