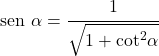このページでは、サイン関数とは何か、その公式、グラフでの表現方法、このタイプの関数の特性、振幅、周期など、サイン関数に関するすべてがわかります。さらに、正弦関数のさまざまな例を見て、概念を完全に理解することができます。正弦定理や正弦関数が他の三角比と持つ関係についても説明しています。
正弦関数の公式
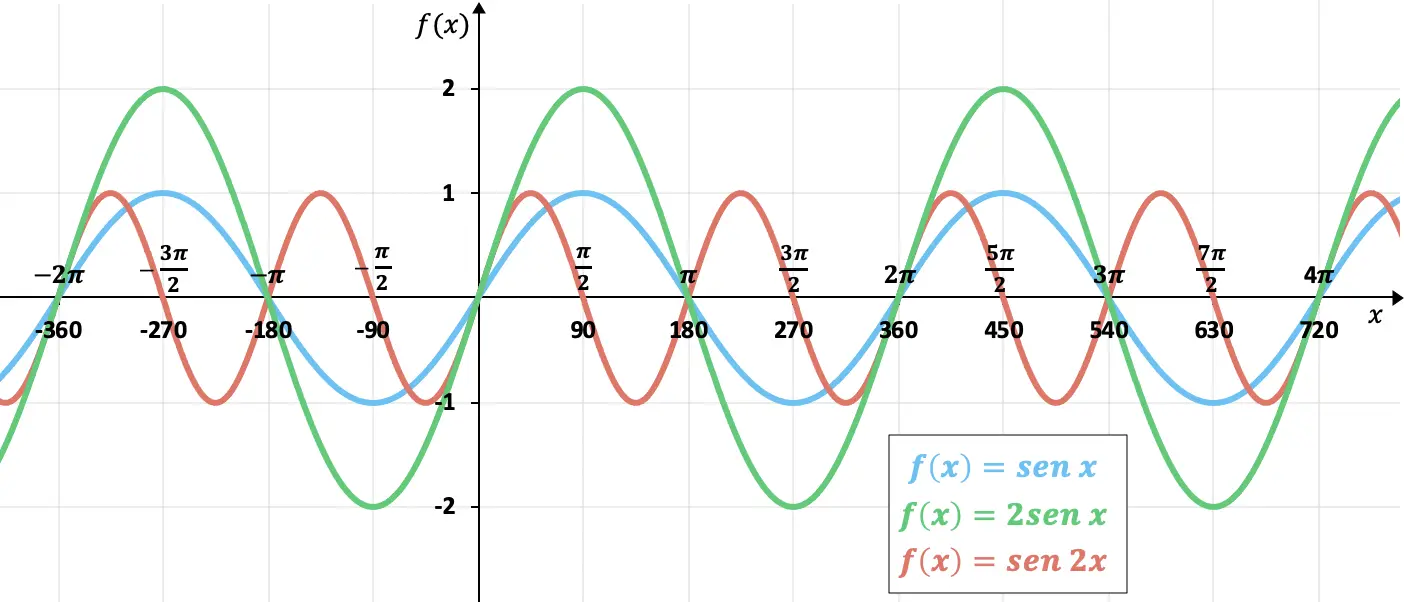
角度αの正弦関数は、直角三角形(直角三角形)の反対側の脚と斜辺との比として式が定義される三角関数です。

このタイプの数学関数は、多くの場合、「sin」または「sin」(ラテン語のsinusに由来)という略語で書かれます。さらに、正弦関数、正弦関数、または正弦波関数と呼ばれることもあります。
サイン関数は、角度のコサインおよびタンジェントと並んで、最もよく知られている三角比の 1 つです。
サイン関数の特性値
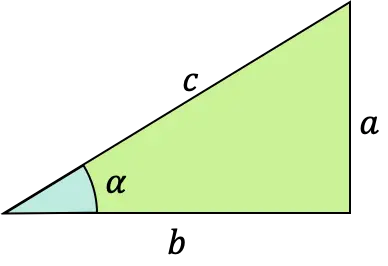
一部の角度は頻繁に繰り返されるため、次の角度での正弦関数の値を知っておくと便利です。
したがって、サイン関数の符号は、角度が位置する象限によって異なります。角度が第 1 象限または第 2 象限にある場合、サインは正になります。一方、角度が第 3 象限または第 4 象限にある場合は、正弦になります。 、正弦は負になります。
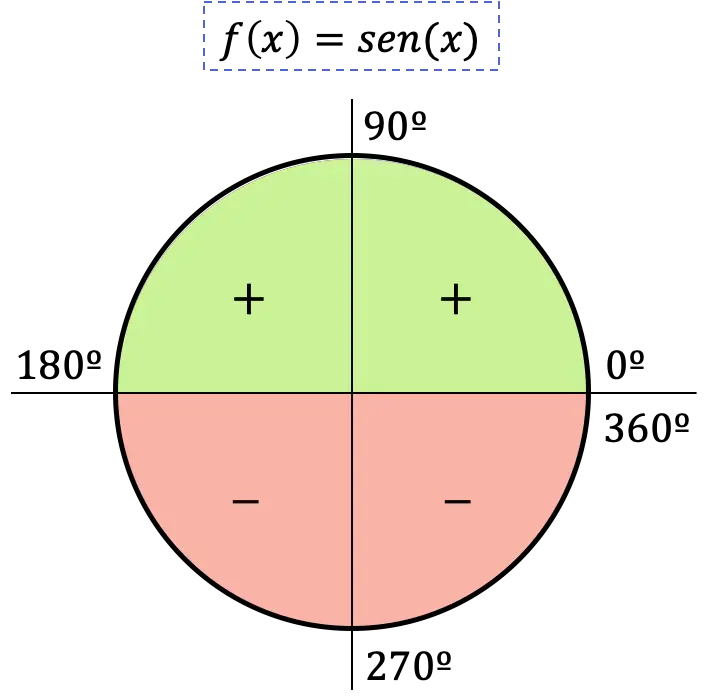
サイン関数のグラフ表示
前のセクションで見た値の表を使用して、正弦関数をグラフ化できます。したがって、サイン関数をグラフにすると、次のようになります。
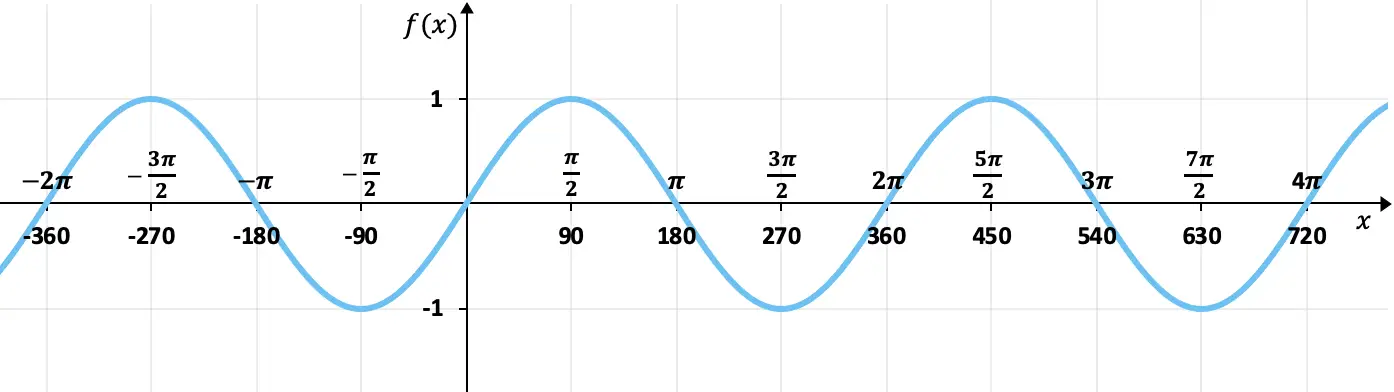
グラフからわかるように、サイン関数の画像の値は常に +1 と -1 の間にあります。つまり、上部は +1 で制限され、下部は -1 で制限されます。さらに、値は 360 度 (2π ラジアン) ごとに繰り返されるため、周期が 360 度の周期関数になります。
一方、このグラフでは、正弦関数が奇数であることが完全に理解できます。これは、正弦関数の反対の要素が反対のイメージを持っているためです。つまり、原点 (0,0) に対して対称です。たとえば、90 度のサインは 1、-90 度のサインは -1 です。
サイン関数のプロパティ
サイン関数には次の特性があります。
- グラフが示すように、関数は独立変数 x の任意の値に対して存在するため、サイン関数の定義域はすべて実数です。
![]()
- サイン関数のパスまたは範囲は、マイナス 1 からプラス 1 (両方を含む) です。
![]()
- これは、周期性 2π を持つ連続奇数関数です。
![]()
- このタイプの三角関数は、点 (0,0) に y 軸 (Y 軸) との交点が 1 つあります。
![]()
- 代わりに、pi のいくつかの座標で横座標 (X 軸) を定期的に切断します。
![]()
- サイン関数の最大値は、次の場合に発生します。
![]()
- 逆に、正弦関数の最小値は次のときに発生します。
![]()
- サイン関数の導関数はコサインです。
![]()
- 最後に、サイン関数の積分は、符号を変更したコサインになります。
![]()
サイン関数の周期と振幅
彼のグラフで見たように、サイン関数は周期関数です。つまり、その値は周波数に従って繰り返されます。さらに、振動する最大値と最小値は振幅によって異なります。したがって、正弦波関数を決定する 2 つの特性は、その周期と振幅です。
![]()
- サイン関数の周期は、グラフが繰り返される 2 点間の距離であり、次の式で計算されます。
![]()
- サイン関数の振幅は、サイン項の前の係数に相当します。
![]()
以下に、周期または振幅を変更した場合の影響を示すグラフを示します。

緑色で示された関数では、振幅を 2 倍にすることにより、関数が +1 から -1 ではなく +2 から -2 になることがわかります。一方、赤で示した関数では、周期が半分になっているため、「標準」サイン関数の 2 倍の速度になっていることがわかります。
正弦定理
サインは通常直角三角形に適用されますが、あらゆる種類の三角形に適用できる定理、sine(s) 定理もあります。
サインの法則は、三角形の辺と角度を次のように関連付けます。
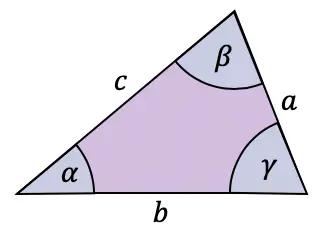
![]()
サイン関数と他の三角比の関係
以下に、三角法で最も重要な三角比と正弦波の関係を示します。
コサイン比
- コサイン関数のグラフはサイン曲線と等価ですが、シフトされています。
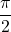
したがって、2 つの関数は次の式で関連付けられます。
![]()
- サインとコサインを三角関数の基本恒等式に関連付けることもできます。
![]()
接線との関係
- 証明するのは複雑ですが、サインは正接に従ってのみ表現できます。
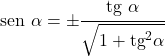
コセカントとの関係
- サインとコセカントは逆乗法です。
![]()
セカントとの関係
- サインを消去して、セカントのみに依存するようにすることができます。
![]()
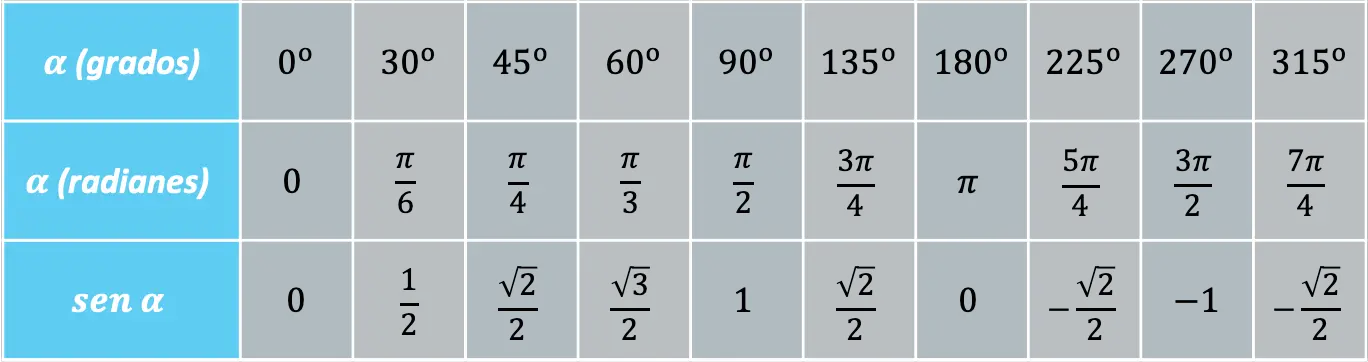
コタンジェントとの関係
- 角度の正弦と余接は、次の方程式によって関係付けられます。