この記事では、関数の横方向の制限とは何かを (例とともに) 説明します。また、関数の左右の横方向の限界をグラフと数値の両方で計算する方法も教えます。さらに、横方向の限界を段階的に解決するエクササイズでトレーニングすることができます。
横方向の制限は何ですか?
ある点における関数の横方向の限界は、その点の周囲での関数の動作を研究します。左横限界と右横限界があり、それぞれ考慮された点の左側と右側の関数の値を分析します。
左右の横方向の制限
側方境界の定義で見たように、左側の側方境界と右側の側方境界の 2 つのタイプがあります。
関数の左限界は、限界を解析する時点でマイナス記号で表され、一方、右限界はプラス記号で示されます。
左側の横方向の限界
![]()
右側の横方向の限界
![]()
横方向の制限の意味をよりよく理解するには、次の例を見てください。
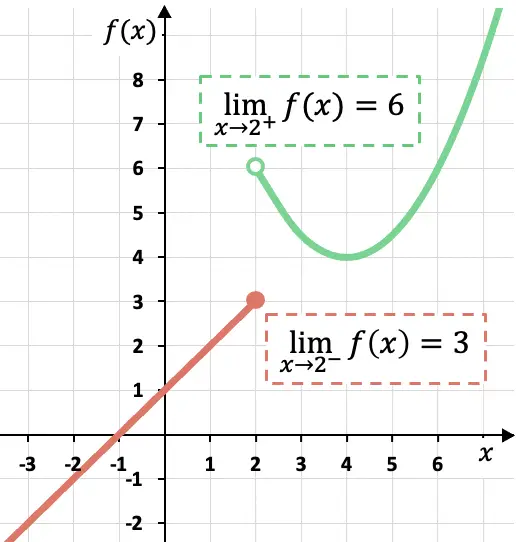
この区分関数のグラフ表示からわかるように、横方向の制限は計算される側によって異なります。
この場合、関数は、x が左から x=2 に近づくにつれて 3 に近い値を取るため、 x が左から 2 に近づくにつれて関数は 3 に近づきます。
一方、直線による x=2 における関数の横方向の限界は 6 の価値があります。その直線によって点 x=2 に近づくと、関数は f(x)= にどんどん近づく値を取るからです。 6.
一方、横方向の制限には通常の制限と同じ特性があることを知っておく必要があります。次のリンクでは、境界プロパティが何であるかを確認できます。
➤参照: 境界プロパティ
等しい横方向の制限
関数の辺の制限が異なる例を見ましたが…辺の制限が同じ場合はどうなるでしょうか?
ある点における関数の両方の横方向の限界が存在し、それらが等しい場合、関数の限界はその点に存在し、その極限の結果は横方向の限界の値になります。
つまり、ある点に関数の限界が存在するには、次の条件が満たされる必要があります。
![]()
したがって、ある点における関数の横方向の限界が異なる場合、その点における関数の限界は存在しません。
また、ある点における関数の極限が存在することは、その関数が点における連続関数であるための必須の条件です。
横方向の制限の概念を理解するために、例を解いてみましょう。

グラフで表された関数の点 x=-2 における横方向の限界は一致します。これは、x=-2 に左から近づくか右から近づくかに関係なく、関数の値が 3 に近づく傾向があるためです。したがって、x=-2 における関数の極限は 3 に等しくなります。
![]()
一方、点 x=4 では、関数は左からは f(x)=3 に近づきますが、右からは関数は f(x)=2 に近づくため、横方向の限界が異なります。したがって、この時点では関数の制限は存在しません。
![]()
横方向の限界の計算
横方向の制限の定義を考慮して、次の例を解くことで、横方向の制限が数値的にどのように計算されるかを確認します。
![]()
通常どおり極限を計算すると、実数を 0 で割った不確定性が得られます。
![]()
ただし、横方向の限界を計算する場合、不確定性は得られません。
![]()
x=2 における関数の横方向の限界を左から計算するには、x=2 より小さいがそれに非常に近い数値 (たとえば、x=1.999) を取得する必要があります。
![]()
この場合、分母は非常に小さい値を持つ負の数になりますが、ゼロではなく、通常はその前にゼロとマイナス記号を付けて表されます。
![]()
したがって、横方向の制限の結果はマイナス無限大になります。数値を 0 で割ると無限大となり、正を負で割ると負になるからです。
![]()
左から x=2 に近い値を持つ関数の画像を計算することで、関数がマイナス無限大に近づいていることを確認できます。
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(1,9)=\cfrac{3}{1,9-2}=-30\\[2ex]f(1,99)=\cfrac{3}{1,99-2}=-300\\[2ex]f(1,999)=\cfrac{3}{1,999-2}=-3000\\[2ex]f(1,9999)=\cfrac{3}{1,9999-2}=-30000\\[2ex]f(1,99999)=\cfrac{3}{1,99999-2}=-300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^-)=-\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-97d799f09c2e0890cf3a856bf9c711a2_l3.png)
同様に、右側の点 x=2 での関数の極限を見つけるには、同じ推論を適用できます。つまり、2 より大きいが非常に近い値 (2001 など) を採用します。
![]()
同様に、右から x=2 に近い値を持つ関数の画像を計算することで、関数が無限大に向かう傾向があることを確認できます。
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(2,1)=\cfrac{3}{2,1-2}=30\\[2ex]f(2,01)=\cfrac{3}{2,01-2}=300\\[2ex]f(2,001)=\cfrac{3}{2,001-2}=3000\\[2ex]f(2,0001)=\cfrac{3}{2,0001-2}=30000\\[2ex]f(2,00001)=\cfrac{3}{2,00001-2}=300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^+)=+\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6d448cdad3ac6ba82e749b30d2bcc11_l3.png)
次のグラフでは、分析された関数が表されていることがわかります。ご覧のとおり、左側の点 x=2 における関数の横方向の限界はマイナス無限大であり、右側の点 x=2 における関数の横方向の限界はプラス無限大です。

横方向の境界の問題が修正されました
演習 1
次の区分的に定義された関数の、定義が変化する点 (x=-2 および x=4) における横方向の限界を求めます。

横方向の限界は点 x=-2 では一致せず、左側では関数は f(x)=5 に向かう傾向があり、一方、右側では関数は定数であり、値は 3 です。
![]()
![]()
x が 4 に近づくにつれて辺の限界も異なります。区分関数は左から 3 に近づきますが、右から -2 に近づきます。
![]()
![]()
演習 2
x が次の区分関数の 3 に近づくときに極限が存在するかどうかを判断し、存在する場合はその値が何かを判断します。
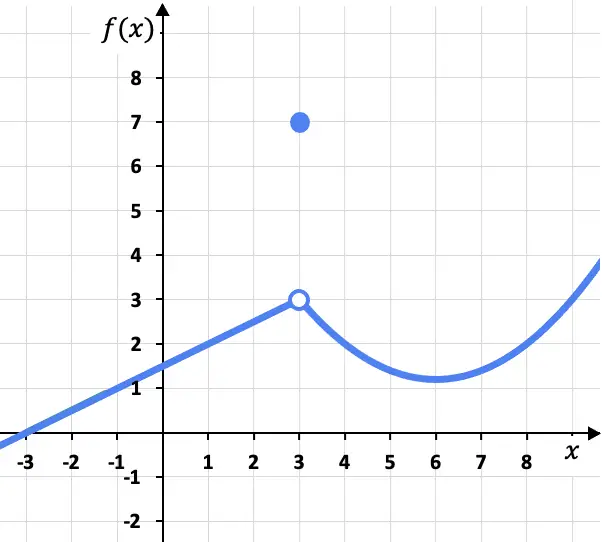
この問題では、左からでも右からでも関数は同じ値 (f(x)=3) に向かう傾向があるため、点 x=3 の左からと右からの横方向の限界は同じです。 。彼の右側:
![]()
![]()
したがって、極限の数学的定義によれば、この同じ点の 2 つの横方向の極限がこの値で一致するため、x が 3 になる傾向があるときの関数の極限は 3 に等しくなります。
![]()
x=3 での関数の限界は 3 ですが、この時点での関数は 3 ではなく、f(3)=7 であることを考慮する必要があります。後で説明するように、これは関数が x=3 で連続的ではなく、回避可能な不連続性があることを意味します。
演習 3
次の有理関数の点 x=4 における横方向の極限を計算します。
![]()
x が左から 4 に向かう傾向がある場合の制限を計算するには、4 より小さいがそれに非常に近い値 (たとえば 3,999) を採用します。
![]()
したがって、x が左から 4 に近づくときの横方向の限界はプラス無限大になります。
そして、x が右から 4 に向かう傾向がある場合の制限を解決するには、関数を 4 より大きく、それに非常に近い値、たとえば 4,001 で評価します。
![]()
したがって、x が右から 4 に近づくときの横方向の限界はマイナス無限大になります。
演習 4
点 x=2 で定義された次の区分関数の極限が存在する場合は、それを求めます。
![\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3 & \text{si} & x \leq 2 \\[2ex]\displaystyle \frac{-3x+5}{x-3} & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”75″ width=”235″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-40d5632016e70b9d9ab8e46e76e0102b_l3.png)