この記事では、有界 (上位および下位) 関数とは何かについて説明します。さらに、関数がある点で制限されることが何を意味するのかを示し、最後にこのタイプの関数のプロパティを示します。
有界関数とは何ですか?
有界関数とは、グラフが範囲内にある関数です。つまり、K (f(x)≤K) を超える関数の値が存在しないような数値 K が存在する場合、関数は上に限定され、次のような数値 K が存在する場合、関数は下に限定されます。関数のすべての値より小さい (f(x)≥K)。したがって、有界関数とは、上下に境界がある関数のことです。
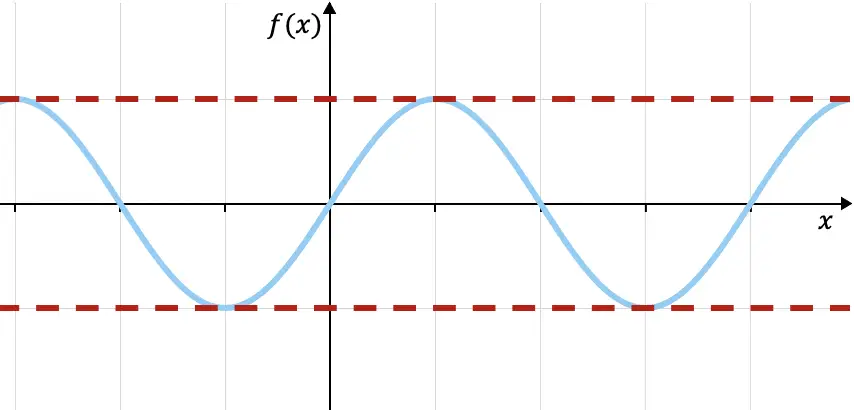
たとえば、上にグラフ化された三角正弦関数は、上部が f(x)=1 で境界付けされ、下部が f(x)=-1 (赤い点線) で境界付けされます。関数はこれら 2 つの制限内にあります。次のリンクで、この関数のその他のプロパティを確認できます。
➤参照:サイン関数の特性
上に制限された関数
ただし、すべての関数が上下に制限されるわけではなく、関数は上下にのみ制限されます。
上記の有界関数は、特定の値を超えない関数、つまり次の条件が満たされる関数です。
![]()
ここで、値 K は関数の上限です。
たとえば、次の放物線は上部が K=7 によって制限されていますが、関数の分岐は無限に伸びているため、関数の下部は制限されていません。

論理的には、関数が K=7 で制限されている場合、関数は K=8 以上の値でも制限されます。
最小の上限は上限と呼ばれ、 sup(f)で表されます。さらに、関数がその領域内で上記の上限に達した場合、この点が関数の絶対最大値であると言えます。
➤参照: 関数の最大値と最小値とは何ですか?
私たちの場合、関数は幾何学的に K=7 によって境界付けられているため、これは関数の上限であり、絶対最大値です。
以下で区切られた関数
以下で区切られた関数は、特定の数値未満の値を持たない関数、つまり次の数式を満たす関数です。
![]()
ここで、K 値は関数の下限です。
以下は、K=3 で区切られた指数関数のグラフ表示です。

明らかに、関数は K=3 未満の値によって制限されます。
前と同様、最大の下限は下限と呼ばれ、 inf(f)で表されます。さらに、関数がその領域内で前記下限に達した場合、この点が関数の絶対最小値であると言えます。
この場合、K=3 は関数の絶対最小値ではありません。関数は無限大でこの値に到達し、したがって関数の領域の外にあるからです。言い換えれば、f(x)=3 は関数 の水平漸近線です。
グラフ表現がなくても、関数が上下で境界があるかどうかを知ることができる定理があります。ワイエルシュトラスの定理とは何かを確認するには、ここをクリックしてください。
➤参照: ワイエルシュトラスの定理
一点で区切られた関数
一般的な関数の境界の概念を学習しましたが、関数がより小さな近傍、つまり関数の一部で境界があるかどうかを分析することもできます。
うん
![]()
は関数の領域内の点であり、
![]()
任意の値の場合、関数はその点で上下に制限されていると言えます。
![]()
環境があれば
![]()
ここで、関数は上下に制限されます。
したがって、関数は次の点で制限されます。
![]()
近傍で上下で区切られている場合
![]()
明らかに、関数が一般に有界であれば、その各点でも有界になります。しかし、その逆は誤りです。つまり、関数はその各点で制限されることはありますが、ドメイン全体にわたって制限されることはありません。
たとえば、次のアフィン関数は各点で部分的に境界がありますが、有界関数ではありません。

有界関数のプロパティ
有界関数には次のプロパティがあります。
- うん

そして

2 つの有界関数、2 つの関数の加算 (または減算) です。
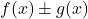
も有界関数です。
- うん

そして

2 つの有界関数、2 つの関数の積です。
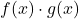
たまたま有界関数でもあります。
- 関数に垂直方向の漸近線がある場合、その関数を完全に制限することはできません。一方、関数は上下に制限することができます。
- 区間上の任意の連続かつ有界関数は積分可能です。