ここでは、関数最適化問題がどのように段階的に解決されるかを説明します。さらに、最適化問題を解く演習で練習することもできます。
最適化問題とは何ですか?
最適化問題は、関数の最大値または最小値を見つけなければならない問題です。たとえば、最適化問題には、企業の利益を定義する関数の最大値の計算が含まれます。
最適化問題の解き方
関数の最適化の問題を解決する手順:
- 最適化が必要な機能を設定します。
- 最適化する関数を導出します。
- 最適化する関数の重要な点を見つけます。これを行うには、関数の導関数をゼロに設定し、結果の方程式を解く必要があります。
- 関数の単調性を調べて、関数の最大値または最小値を決定します。
最適化問題の例
最適化問題の理論を考慮して、このタイプの問題を段階的に解決して、どのように実行されるかを見ていきます。
- 脚の合計が10cmの直角三角形のうち、表面積が最大のものの寸法を計算します。
この問題を解決するために、三角形の 1 つの分岐をxと呼び、もう 1 つの分岐をyと呼びます。

ステップ 1:最適化する機能を設定します。
三角形の面積を最大にする必要があり、三角形の面積の公式は次のとおりです。
![]()
この場合、三角形の底辺はx 、高さは y です。まだ:
![]()
最適化する関数はすでにありますが、この関数は 2 つの変数に依存しますが、依存できるのは 1 つだけです。ただし、2 つの脚の合計は 10 cm でなければならないと記載されています。まだ:
![]()
この方程式からyを解きます。
![]()
そして、その式を関数に代入します。
![]()
![]()
これで、計画された最適化関数が完成しました。この関数は 1 つの変数にのみ依存するため、次のステップに進むことができます。
ステップ 2:最適化する関数の導関数を計算します。
これは有理関数なので、除算の導関数の公式を適用して導出します。
![]()
![]()
ステップ 3:重要なポイントを見つけます。
関数の臨界点を見つけるには、導関数をゼロに設定し、結果として得られる方程式を解く必要があります。
![]()
![]()
4 は左側全体を除算するので、右側全体を乗算することで乗算できます。
![]()
![]()
![]()
![]()
![]()
ステップ 4:関数の単調性を調べ、関数の最大値または最小値を決定します。
関数の単調性を調べるために、右側にある臨界点を表します。
次に、各区間の導関数の符号を評価して、関数が増加しているか減少しているかを確認します。これを行うには、各区間の点 (臨界点ではない) を取得し、その点で導関数がどのような符号を持つかを調べます。
![]()
![]()
![]()
導関数が正の場合、関数が増加していることを意味し、導関数が負の場合、関数が減少していることを意味します。したがって、関数を増減する間隔は次のようになります。
成長:
![]()
減少:
![]()
x=5 では、関数は増加から減少に移行するため、 x=5 は最適化される関数の相対最大値です。
したがって、x=5 が最大面積を持つ三角形の枝の値になります。もう一方の脚の値を単純に計算します。
![]()
結論として、三角形の最大面積を最大化する値は次のとおりです。
![]()
![]()
最適化の問題が解決されました
問題 1
その薬は病気の人に与えられ、
![]()
数時間後の有効成分の血中濃度は次の関数で求められます。
![]()
ミリリットルあたりのミリグラム。の最大値を決定します。
![]()
そして、その値に達したときを示します。
ステップ 1: 最適化する機能を設定します。
この問題では、提案された関数がすでに与えられています。
![]()
ステップ 2: 最適化する関数の導関数を計算します。
この関数は 2 つの関数の積で構成されます。したがって、関数の導関数を計算するには、積の導関数のルールを適用する必要があります。
![]()
![]()
ステップ 3: 重要なポイントを見つけます。
関数の臨界点を見つけるために、次を解決します。
![]()
![]()
![]()
共通因数を使って方程式を解きます。
![]()
乗算が 0 になるには、乗算の 2 つの要素のうちの 1 つがゼロでなければなりません。したがって、各係数を 0 に設定します。
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
数値を別の数値に累乗しても 0 になることはありません。したがって、
![]()
解決策はありません。
ステップ 4: 関数の単調性を調べ、関数の最大値または最小値を決定します。
関数の単調性を調べるために、右側にある臨界点を表します。
次に、各区間の導関数の符号を評価して、関数が増加しているか減少しているかを確認します。したがって、各区間の点 (臨界点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
微分値が正の場合は関数が増加することを意味し、一方、微分値が負の場合は関数が減少することを意味します。したがって、最適化される関数の増加と減少の間隔は次のようになります。
成長:
![]()
減少:
![]()
関数は t=2 で増加から減少に転じるため、 t=2 が関数の最大値になります。したがって、最大濃度には t=2 時間で到達します。
最後に、最大値が発生する値を元の関数に代入して、最大濃度の値を求めます。
![]()
問題 2
ある店は電動スクーターを 40 台、1 台あたり 1,000 ユーロの価格で販売したいと考えています。しかし、市場調査によると、スクーターの価格が 50 ユーロ下がるごとに、ベストセラー スクーターのトップ 10 の売上が増加します。
まず、スクーターの元の 1,000 ドルの価格が 50 ドル値下げされる回数に基づいて、店舗の収益関数を作成します。次に、最大の利益が得られるスクーターの価格と、その価格で得られる収益を決定します。
ステップ 1: 最適化する機能を設定します。
問題文は、この関数が初期価格が 50 ドル減額される回数に依存する必要があることを示しているため、ヒントを与えてくれます。したがって、価格が €50 減額される回数を x と呼びます。
![]()
ユーロ
収益関数は、販売されたスクーターの数に各スクーターの価格を乗じたものになります。
![]()
販売されるスクーターの台数は 40 台で、さらに 50 ユーロの値下げごとに 10 台のスクーターが販売されます。まだ:
![]()
各スクーターの価格は開始時に 1000 ユーロで、価格が下がるたびに 50 ユーロずつ下がります。まだ:
![]()
したがって、問題を最適化する関数は次のようになります。
![]()
![]()
![]()
![]()
ステップ 2: 最適化する関数の導関数を計算します。
多項式関数であるため、導関数は計算が簡単です。
![]()
ステップ 3: 関数の重要なポイントを見つけます。
関数の臨界点を見つけるために、次を解決します。
![]()
![]()
![]()
![]()
![]()
ステップ 4: 関数の単調性を調べ、関数の最大値または最小値を決定します。
関数の単調性を調べるために、数直線上で計算された臨界点を表します。
次に、各区間の導関数の符号を評価して、関数が増加しているか減少しているかを確認します。したがって、各区間の点 (臨界点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
導関数が正の場合、関数が増加していることを意味し、導関数が負の場合、関数が減少していることを意味します。したがって、成長と衰退の間隔は次のようになります。
成長:
![]()
減少:
![]()
関数は x=8 で増加から減少に転じるため、 x=8 が関数の最大値となります。したがって、 50ユーロの減額の8倍で最大の収入が得られることになります。
ここで、最大収入が現れる値を元の関数に代入して、最大収入の値を求めます。
![]()
![]()
ユーロ
50 ユーロの割引を 8 回行った後の各スクーターの価格は次のようになります。
![]()
![]()
ユーロ
問題 3
企業のコスト関数 (単位は数千ユーロ) は、次の式を使用して決定できます。
![]()
金
![]()
特定の品目から生産された数千単位を表します。
コストを最小限にするにはどれくらいの量を生産する必要があるか、そのコストはいくらか、これらのアイテムがまったく生産されなかった場合のコストはいくらになるかを決定します。
ステップ 1: 最適化する機能を設定します。
問題ステートメントは、最適化される関数をすでに提供しています。
![]()
ステップ 2: 最適化する関数の導関数を計算します。
![]()
ステップ 3: 重要なポイントを見つけます。
関数の臨界点を見つけるために、次を解決します。
![]()
![]()
![]()
![]()
![]()
ステップ 4: 関数の単調性を調べ、関数の最大値または最小値を決定します。
右側にある重要な点を表します。
次に、各区間の導関数の符号を評価して、関数が増加しているか減少しているかを確認します。したがって、各区間の点 (臨界点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
導関数がゼロより大きい場合、関数はこの区間にわたって増加します。一方、導関数がゼロより小さい場合、関数はこの区間で減少します。したがって、関数の増加と減少の間隔は次のようになります。
成長:
![]()
減少:
![]()
この関数は x=3 で減少から増加に変わるため、 x=3 が関数の最小値となります。したがって、最小コストは3,000 個の生産によって達成されます。
ここで、最小コストに達する値を元の関数に代入して、最小コスト値を見つけます。
![]()
数百万ユーロ。
一方で、何も生産されなかった場合、つまりいつ生産された場合のコストはいくらになるのかを尋ねます。
![]()
したがって、計算する必要があります
![]()
![]()
数百万ユーロ。
問題4
2 m 2の領域を区切る長方形の木製フレームを構築したいと考えています。木材の価格は、水平方向の場合は 7.5 ユーロ/m、垂直方向の場合は 12.5 ユーロ/m であることがわかります。フレームの総コストが可能な限り最小になり、そのコストが最小になるように、長方形に必要な寸法を決定します。
ステップ 1: 最適化する機能を設定します。
この問題を解決するために、水平辺をx 、垂直辺をyと呼びます。

水平面の購入には 7.5 ユーロ、垂直面の購入には 12.5 ユーロがかかります。さらに、各フレームには 2 つの水平辺と 2 つの垂直辺が必要です。したがって、フレームのコストは次の関数で決定できます。
![]()
最適化する機能はすでにあります。ただし、1 つの変数にしか依存できない場合、2 つの変数に依存します。ただし、この声明によれば、フレームの表面積は 2 m 2でなければなりません。まだ:
![]()
変数yを削除します。
![]()
そして、最適化する関数内で見つかった式を次のように置き換えます。
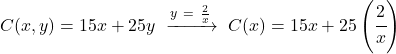
![]()
ステップ 2: 最適化する関数の導関数を計算します。
![]()
ステップ 3: 重要なポイントを見つけます。
関数の臨界点を見つけるために、次を解決します。
![]()
![]()
![]()
![]()
![]()
![]()
分数を使って方程式を解くために横に乗算します。
![]()
![]()
![]()
![]()
![]()
ステップ 4: 関数の単調性を調べ、関数の最大値または最小値を決定します。
直線上の関数の単調性を分析するために見つかった臨界点を表します。
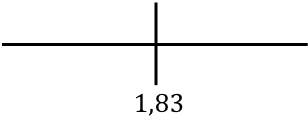
次に、各区間の導関数の符号を評価して、関数が増加しているか減少しているかを確認します。したがって、各区間の点 (臨界点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
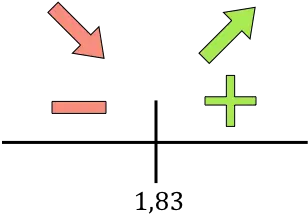
導関数が正の場合、関数が増加していることを意味し、導関数が負の場合、関数が減少していることを意味します。したがって、成長と衰退の間隔は次のようになります。
成長:
![]()
減少:
![]()
関数は x=1.83 で減少から増加に変化するため、 x=1.83 が関数の最小値になります。
したがって、x=1.83 が最小コストを表す横辺の値になります。次に、垂直辺の値を計算してみましょう。
![]()
したがって、最小フレームワークコストを構成する値は次のとおりです。
水平方向の側面
![]()
垂直面
![]()
これらの値で到達する最小コストは次のとおりです。
![]()
ユーロ
問題5
次の図に示すように、大聖堂の扉は 2 本の柱で支えられた半円形のアーチで形成されています。
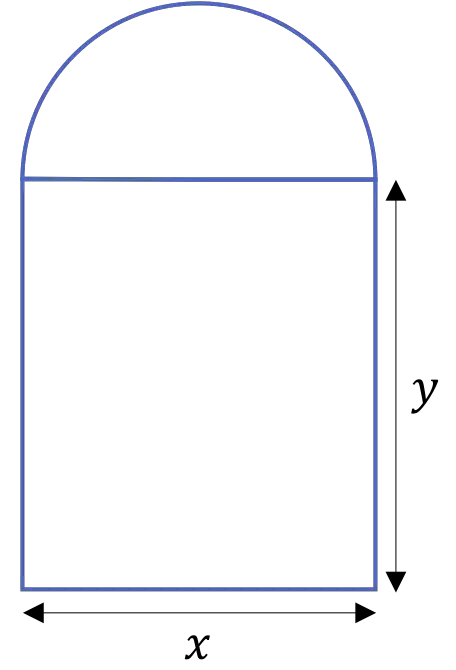
ドアの周囲が 20 m の場合、寸法を決定します。
![]()
そして
![]()
ドア全体の表面積を最大化します。
ステップ 1: 最適化する機能を設定します。
円の面積は次の式で計算されます。
![]()
したがって、ドア全体の面積は、長方形の面積に円周の半分の面積を加えたものになります。
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
最適化する機能はすでにあります。ただし、1 つの変数にしか依存できない場合、2 つの変数に依存します。
ただし、リリースによれば、ゲート全体の周囲は20メートルです。円の周長は次の式で計算されます。
![]()
したがって、ドア全体の周囲の長さは次のようになります。
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
周囲は20メートルでなければなりません。したがって、前の式を 20 に設定して、次の関係を調べます。
![]()
そして
![]()
![]()
すべての項に 2 を掛けて、端数を削除します。
![]()
![]()
クリアします
![]()
![]()
![]()
そして、最適化する関数内で見つかった式を次のように置き換えます。
![]()
![]()
![]()
ステップ 2: 最適化する関数の導関数を計算します。
![]()
![]()
ステップ 3: 重要なポイントを見つけます。
関数の臨界点を見つけるために、次を解決します。
![]()
![]()
![]()
これは分数を含む方程式なので、各項に分母の lcm を乗算して分数を消去します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ステップ 4: 関数の単調性を調べ、関数の最大値または最小値を決定します。
関数の単調性を調べるために、右側にある臨界点を表します。
次に、各区間の導関数の符号を評価して、関数が増加しているか減少しているかを確認します。したがって、各区間の点 (臨界点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
導関数が正の場合、関数が増加していることを意味し、導関数が負の場合、関数が減少していることを意味します。したがって、成長と衰退の間隔は次のようになります。
成長:
![]()
減少:
![]()
関数は x=5.6 で増加から減少に転じるため、 x=5.6 が関数の最大値となります。
まだ、
![]()
最大の面を作る値です。次に、次の値を計算します。
![]()
![]()
したがって、最大表面を構成する値は次のとおりです。
![]()
![]()
問題6
面積 54 cm 2の円筒形のタンクを構築したいと考えています。体積が最大になるように、底面の半径と円柱の高さを決定します。
ステップ 1: 最適化する機能を設定します。
シリンダーの体積は次の式で計算されます。
![]()
底面の面積は円なので、式は次のようになります。
![]()
。したがって、シリンダーの体積の公式は次のようになります。
![]()
最適化する機能はすでにあります。しかし、それは 2 つの変数に依存します (
![]()
そして
![]()
) 一方、依存できるのは 1 つだけです。ただし、このステートメントでは、円柱の面積は 54 cm 2でなければならないと述べているため、この条件を利用して次の関係を求めます。
![]()
そして
![]()
円柱の面積を計算するには、その側面積と 2 つの底面の面積を加算する必要があります。
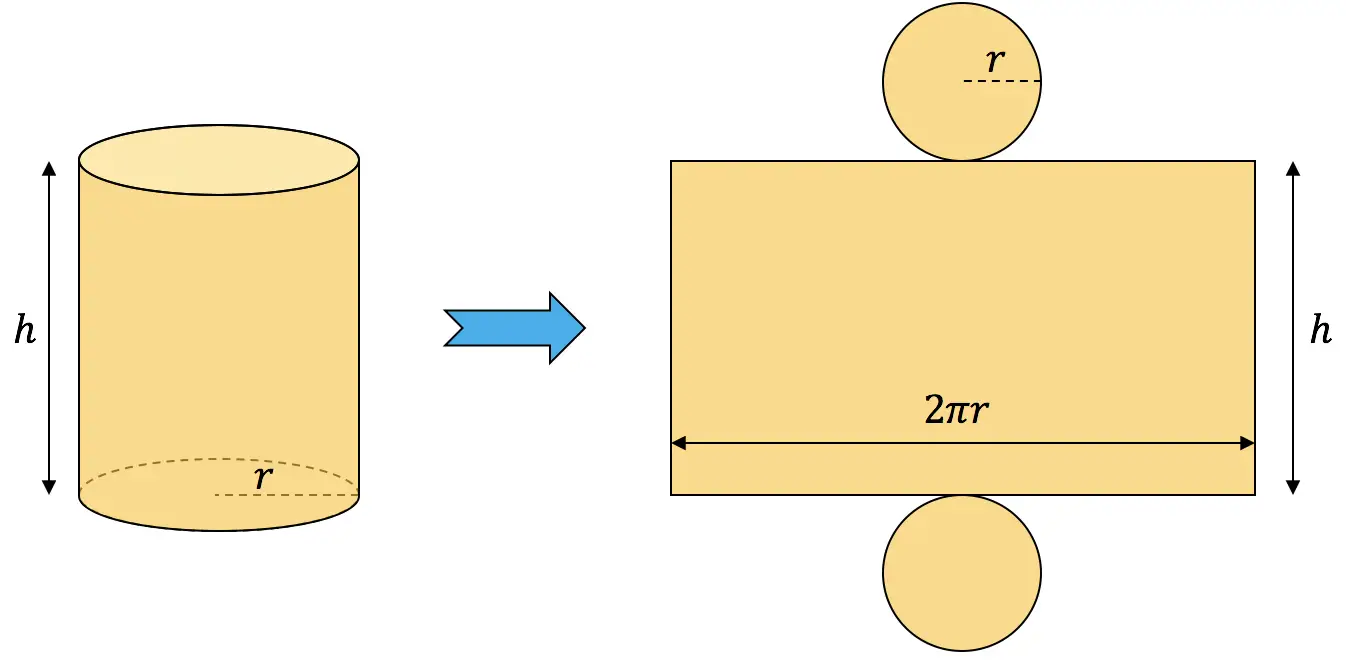
![]()
円柱の面積は 54 cm 2である必要があるため、前の式を 54 に設定して、次の関係を取得します。
![]()
そして
![]()
![]()
クリアします
![]()
![]()
![]()
そして、最適化する関数内で見つかった式を次のように置き換えます。
![]()
![]()
![]()
ステップ 2: 最適化する関数の導関数を計算します。
![]()
ステップ 3: 重要なポイントを見つけます。
関数の臨界点を見つけるために、次を解決します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ステップ 4: 関数の単調性を調べ、関数の最大値または最小値を決定します。
関数の単調性を調べるために、数直線上にある臨界点を表します。
次に、各区間の導関数の符号を評価して、関数が増加しているか減少しているかを確認します。したがって、各区間の点 (臨界点ではない) を取得し、この点で導関数がどのような符号を持つかを調べます。
![]()
![]()
導関数が正の場合、関数が増加していることを意味し、導関数が負の場合、関数が減少していることを意味します。したがって、成長と衰退の間隔は次のようになります。
成長:
![]()
減少:
![]()
この関数は r=1.69 で増加から減少に転じるため、 r=1.69 cm が関数の最大値になります。
したがって、r=1.69が最大体積を作る半径の値となります。次に高さを計算します。
![]()
したがって、最大音量となる値は次のとおりです。
無線
![]()
身長
![]()