最小二乗法は、一連の点に対応する最適な直線を見つけるための数学的ツールです。それを簡単に説明します。
グラフ上に点があちこちに点在していると想像してください。線と点の間の距離を最小限に抑えるために、これらの点に最もよく「適合」する直線を見つけたいとします。これが最小二乗法の背後にある考え方です。
この方法では、数式を使用して、点と直線の差の二乗和を最小にする直線の方程式を計算します。つまり、点からの「偏差」が最も小さい線を探します。
簡単に言えば、最小二乗法は調査中に得られたデータの分析に役立ち、彼らの行動を線形的に表現し、盗まれた情報のエラーを減らすことを目的としています。
最小二乗法を考案したのは誰ですか?
統計およびデータ分析の基本ツールである最小二乗法は、1794 年に提案したドイツの数学者カール フリードリヒ ガウスによるものとされています。ただし、ガウスがそれを発表したのは1809 年でした。
興味深いことに、フランスの数学者アンドリアン・マリー・ルジャンドルは、独自に開発して同様のバージョンを 1805 年に出版しました。
両数学者は、モデルを観察データに適合させ、正確な予測を行うためにさまざまな分野で広く使用されているこの手法の作成に貢献しました。
最小二乗の公式
この方法が何を意味するのかを理解するには、その公式とその実装プロセスを説明することが不可欠であることは間違いありません。最小二乗公式の詳細な説明は次のとおりです。
問題を定義する
独立変数 (x) と従属変数 (y) という 2 つの変数を含むデータ セットがあり、このデータに直線を近似したいとします。
目的は、y の実際の値と、y によって予測される値との差の二乗和を最小にする直線の方程式の係数の値 (切片と傾き) を見つけることです。フィットしたライン。
直線の方程式を計算します
直線の方程式は y = mx + b の形式になります。ここで、m は傾き、b は y 切片です。 myb 値を計算するための最小二乗公式は次のとおりです。
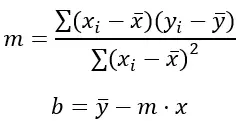
金:
Σは値の合計を表します。
x iと y iは、それぞれ各データ点の変数 x と y の値です。
x̄ と ϳ は、それぞれ x と y の値の平均です。
(x i – x̄) と (y i – ϳ) は、x と y の値の差とそれぞれの平均です。
(x i – x̄) 2 は、 x の値とその平均の差の 2 乗です。
結果を解釈する
式を使用して m と b の値を計算したら、それらを使用して近似直線の方程式を取得できます。たとえば、m = 2 および b = 3 の場合、近似直線の方程式は y = 2x + 3 になります。これにより、x のさまざまな値に対する y の値の予測または推定が可能になります。調整された右側に基づいて。
最小二乗法はいつ使用されますか?
おそらく、この方法はいつ使用されるのかと自問するでしょう。様々な場面で大活躍!たとえば、実験データや研究データを分析して関係性や傾向を見つけたい場合です。
家の価格とその平方メートル単位の広さの関係を調査しているとします。最小二乗法を使用すると、データに最もよく適合する直線を見つけることができ、この関係を明確に把握できます。
経済学でも、製品需要や価格動向などの変数をモデル化し、予測するために使用されます。さらに、エンジニアリングでは、数学的モデルをテストまたはシミュレーション データに適合させるために最小二乗法が適用されます。
最小二乗法は、データを分析して重要な関係を見つけるために、多くの研究分野や仕事で使用される強力で汎用性の高いツールです。
最小二乗法の他の定理への応用
最小二乗法は、それ自体で使用されるだけでなく、他の定理でも非常に役立ちます。以下で、この件についてもう少し詳しく見てみましょう。
回帰定理
これは、一連のデータに適合する最適な直線を見つけるための回帰定理で広く使用されています。たとえば、これを使用して植物の高さと植物が受け取る光の量の関係を分析し、さまざまな照明条件で植物がどのように成長するかを判断できます。
定理補間
この場合、点のセットに最もよく適合する多項式関数を見つけるために、最小二乗法が内挿定理にも適用されます。たとえば、位置と時間のデータに基づいて移動オブジェクトの軌道を近似するために使用できます。
カーブフィッティング定理
これは、一連のデータに適合する曲線を見つけるために曲線近似定理で使用されます。これは、気候変動を予測したり、発射体の軌道を予測するための気候データのモデリングなどのアプリケーションに役立ちます。
フーリエ解析定理
フーリエ解析定理では、最小二乗法を使用して、一連の離散データから周期関数を近似します。これは、データ シグナリングと画像と音声の圧縮に当てはまります。
非線形回帰定理
最後に、最小二乗法は非線形回帰定理にも適用され、線形関係に従わないデータセットに適合する最適な曲線を見つけます。たとえば、化学物質の濃度が反応速度にどのような影響を与えるかを分析するために使用できます。
最小二乗法の例
最小二乗法の適用方法をより深く理解するために、以下の例を見てみましょう。
さまざまな週の植物の次の高さデータ (センチメートル単位) があるとします。
| 週 | 身長(センチメートル) |
| 1 | 十 |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | 二十 |
将来の植物の高さを予測するために、このデータに適合する最適な直線を見つけたいと考えています。
ステップ 1 : データをグラフ化する
最初に行うことは、散布図にデータをプロットすることです。 X 軸は週を表し、Y 軸は身長をセンチメートル単位で表します。グラフは次のとおりです。
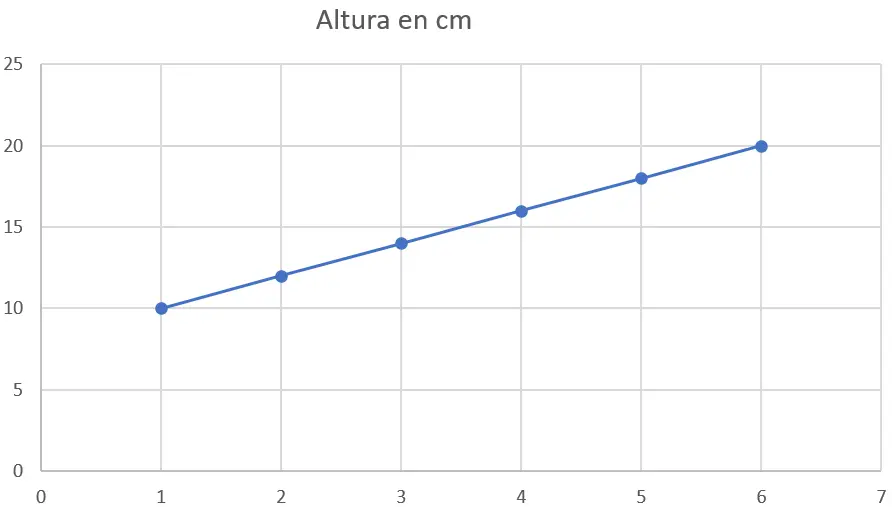
ステップ 2 : 最小二乗法を適用する
最小二乗法は、実際のデータと直線によって予測される値との差の二乗和を最小化する直線を見つけようとします。この場合、線は線の方程式 y = mx + b で表されます。ここで、「y」は高さ、「x」は週、「m」は線の傾き、「b」はy 切片。
差の二乗和を最小にする「m」と「b」の値を見つけるには、次の式が使用されます。
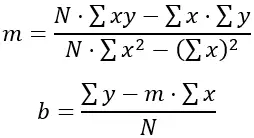
ここで、N はデータ ポイントの数 (この場合は 6)、Σxy は週の合計と高さの積、Σx は週の合計、Σy は高さの合計、Σx 2は週の二乗の合計です。 。
これらの式を高さデータに適用すると、次の結果が得られます。
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
これらの値を「m」と「b」の式に代入すると、次のようになります。
m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 2 ) ≈ 2.07
b = (90 – 2.07 · 21) ÷ 6 ≈ 3.24
したがって、高さデータに対応する直線の方程式は y となります。