このページでは、整列点とは何かについて説明します。また、3 つ (またはそれ以上) の点が揃っているかどうかを判断するために利用できるすべての方法も表示されます。さらに、練習できるように、いくつかの例と解決された練習問題も見つかります。
点が揃っているとはどういう意味でしょうか?
解析幾何学では、 3 つ以上の点がすべて同じ線上にある場合、つまり、点間に直線を引くことによって点を結ぶことができる場合、それらの点は整列していると見なされます。
2 点間にはいつでも線を引くことができるので、2 点は常に整列します。ただし、3 つの点が同一線上にある必要はありません。 3 つ以上の点が揃っているかどうかを確認するには、主に 2 つの方法があります。
- ベクトル法: 点を形成するベクトルが比例しているかどうかを確認することから構成されます。
- 直線方程式法: 点が同じ直線に属するかどうかを判断することで構成されます。
以下に各手順の説明と例を示しますので、どれが最適かを判断してください。
3 つ (またはそれ以上) の点がベクトル法で位置合わせされているかどうかを確認する方法
次の 3 つの点を考慮してください。
![]()
ベクトルが次の場合、3 つの点は整列します。
![]()
そして
![]()
それらは同じ方向を持っています。つまり、それらのコンポーネントが比例しているかどうかです。
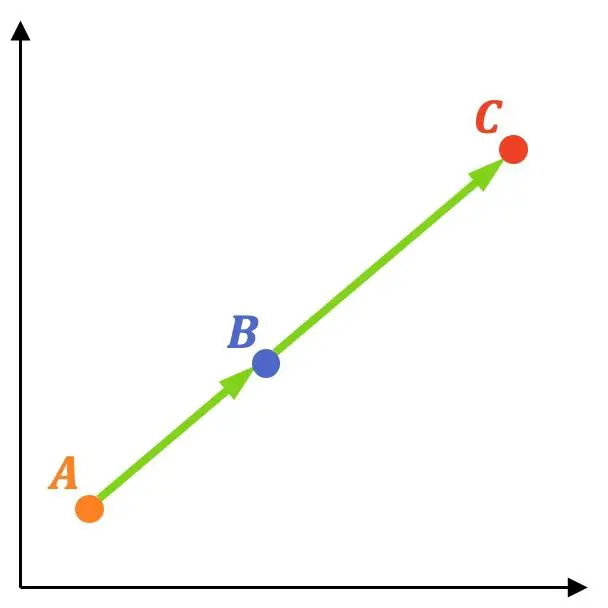
これがどのように行われるかの例を見てみましょう。
- 次の 3 点が揃っているかどうかを確認します。
![]()
まず、点間のベクトルを計算します。 2 つの異なるベクトルを計算するだけで十分です。
![]()
![]()
次に、ベクトルの座標が比例しているかどうかを確認します。
![]()
2 つのベクトルの X 成分と Y 成分を除算すると、同じ結果 (-2) が得られます。したがって、ベクトルは同じ方向を持ち、したがって点は整列します。
このメソッドは、空間 (R3) 内で 3 つ以上の点が整列しているかどうかを確認するためにも使用できます。追加する必要があるのは、2 つのベクトルの 3 番目の成分 (Z 成分) も比例しているかどうかを確認することだけです。
この記事が役立つ場合は、おそらく2 点の中点を計算する方法についても興味があるでしょう。なぜなら、2 点の中点を見つけることは、他の 2 点と並んだ 3 番目の点を決定する方法であることは明らかだからです。リンクされたページでその方法を確認することができ、さらに、段階的に解決された例や演習も確認できます。
直線方程式法で 3 つ (またはそれ以上) の点が揃っているかどうかを確認する方法
前のセクションで説明したように、3 つ以上の点の位置合わせを研究する 1 つの方法は、それらの点の間に形成されるベクトルを使用することです。そうですね、もう 1 つの方法は、直線の方程式から始めることです。
次の 3 つの点を考慮してください。
![]()
3 つの点がすべて同じ直線に属している場合、その点は位置合わせされます。したがって、3 つ以上の点が揃っているかどうかを確認するには、次の手順に従う必要があります。
- 3 点のうち 2 点を通る直線の方程式を求めます。
- 3 番目の点もラインに属しているかどうかを確認します。この場合は3点が揃っていることを意味しますが、条件を満たさない場合は点が揃っていないことを意味します。
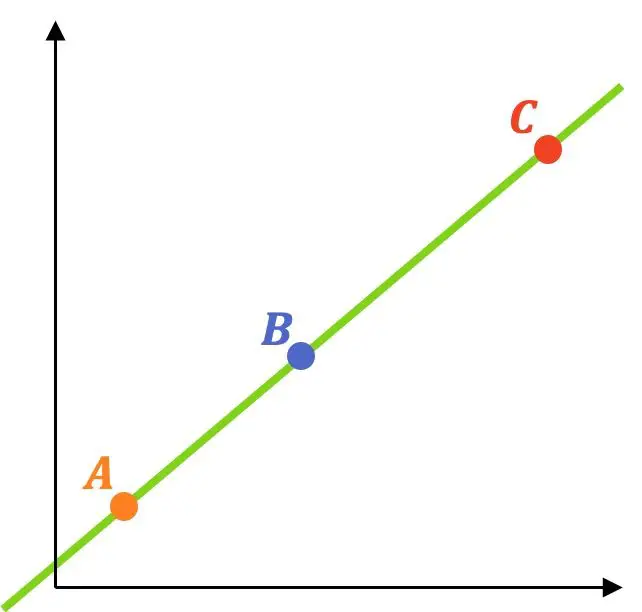
例として、次の方法を使用して演習を解きます。
- 以下の3点が揃っていることを確認してください。
![]()
まず、点 A と B を通過する直線の方程式を計算する必要があります。したがって、直線の方向ベクトルを求めます。
![]()
次に、直線の方程式を構築する必要があります。パラメトリック、暗黙的、一般など、必要なタイプを選択できます。ただし、この場合は連続方程式を使用します。したがって、点 A と点 B を通る直線の連続方程式は次のようになります。
![]()
直線の方程式が得られたら、他の点も同じ直線に属しているかどうかを確認する必要があります。これを行うには、点 C の座標を直線の方程式に代入します。
![]()
![]()
![]()
同点になったので、ポイントはラインの方程式を満たします。したがって、 3 つの点は同一線上にあります。
整列した点のセットは等距離である必要はなく、整列したいくつかの点間の距離は異なっていてもよいことに注意してください。 2 つの概念の違いは、2 点間の距離 (幾何学)の説明で確認できます。また、段階的に解決される例と演習も参照できます。
整列ドット演習を解決しました
演習 1
次の 3 点が揃っているかどうかを確認します。
![]()
問題を解決するには、これまでに説明した 2 つの方法のうち 1 つを選択できます。この場合、ベクトル法を使用します。
まず、点間のベクトルを計算します。
![]()
![]()
次に、ベクトルのデカルト座標が比例しているかどうかを確認します。
![]()
2 つのベクトルの X 成分と Y 成分を互いに除算すると、同じ結果 (-4) が得られるため、ベクトルは同じ方向になります。点が揃っていることを示す事実。
演習 2
3 つのポイントを与えると:
![]()
次の 2 つの点にどれが一致するかを判断します。
![]()
この場合、直線方程式法を使用するため、いくつかの計算が省略されます。
したがって、点 D と点 E を通過する直線の連続方程式を計算します。
![]()
![]()
次に、どの点が直線の方程式に対応し、したがって点 D および E と一致するか、またどの点が一致しないかを確認してみましょう。
ポイント A を確認します。
![]()
![]()
![]()
直線の方程式は真ではないため、点 A は点 D および点 E と一致しません。
次にポイント B を確認します。
![]()
![]()
![]()
この場合、直線の方程式が満たされるため、点 B は点 D および点 E と同一直線上にあります。
そして最後に、ポイント C でプロセスを繰り返します。
![]()
![]()
![]()
直線の方程式は真ではないため、点 C は点 D および E と整列しません。
演習 3
未知の価値を見つける
![]()
次の 3 点が揃うようにします。
![]()
この場合、ベクトル法を使用します。
したがって、点間のベクトルを計算しようとします。
![]()
![]()
3 点の共線性が満たされるためには、2 つのベクトルの座標が比例する必要があります。したがって、次の条件を適用します。
![]()
そして、次の方程式を解きます。
![]()
![]()
![]()
![]()
![]()
![]()
3点が揃うように
![]()
2の価値がある必要があります。