▷ 数値の階乗: それは何か、そしてその計算方法 ✅

このページでは、数値の階乗とは何か、およびその計算方法について説明します。さらに、いくつかの例と、最も使用される階乗の値を示す表が示されています。また、電卓を使って数値の階乗を計算する方法も教えます。最後に、階乗の応用と特性を示します。

数値の階乗とは何ですか?

数学では、数値の階乗は、1 からその数値までのすべての正の整数の積に等しくなります。さらに、数値の階乗は、数値の後の感嘆符 (!) で表されます。

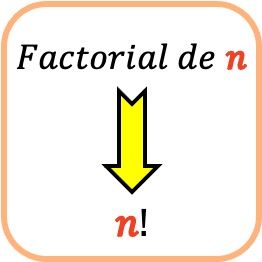
たとえば、数値nの階乗 (階乗nとも呼ばれます) を求めるには、数値nにその前にあるすべての整数 (1 から始まる) を乗算する必要があります。

$n! = 1 \cdot 2 \cdot 3 \cdots (n-2) \cdot (n-1) \cdot n$

数値の階乗を計算する方法

数値の階乗の意味を理解したら、例を使って階乗を決定する方法を見てみましょう。

4 の階乗を計算します。

数学的定義で見たように、数値の階乗は、それ以下のすべての正の整数の乗算と同等です。したがって、4 の階乗を計算するには、数値 1、2、3、4 を掛ける必要があります。

$4! = 1 \cdot 2 \cdot 3 \cdot 4 =24$

したがって、4 の階乗は 24 になります。

数値の階乗の例

数値の階乗の概念を理解するために、異なる数値のいくつかの階乗を計算する例を示します。

3 の階乗:

$3! = 1 \cdot 2 \cdot 3 =6$

5 の階乗:

$5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5=120$

6 の階乗:

$6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6=720$

1 の階乗:

$1! = 1$

論理的には、1 を乗算すれば十分であるため、数値 1 の階乗は 1 に等しくなります。

0 の階乗:

$0! = 1$

はい、わかりました。驚くべきことに、0 の階乗は 0 ではなく 1 です。理論的には 0 に 1 を掛ける必要があるため、これは少し奇妙に思えるかもしれません。しかし、慣例として 0 が採用されています。 =1。製品プロパティが空であるためです。さらに詳しく知りたい場合に備えて、このリンクを残しておきます。理由を知っているかどうかはあまり関係ありませんが、重要なことは、 0 の階乗は 1 に等しいということを覚えておくことです。

数値の階乗の結果のリスト

以下に、最もよく使用される数値の階乗を表にまとめましたので、手で計算する必要はありません。

人数、個数、総数	数値の階乗
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5,040
8	40,320
9	362,880
十	3,628,800
十一	39,916,800
12	479,001,600
13	6,227,020,800
14	87 178 291 200
15	1,307,674,368,000
16	20,922,789,888,000
17	355,687,428,096,000
18	6,402,373,705,728,000
19	121,645,100,408,832,000
二十	2,432,902,008 176,640,000
50	3,041,409,320 · ^10.64
100	9,332 621,544 · ^10,157
1,000	4,023,872,601 · ^10.2567
10,000	2,846,259,681 · ^10,35,659
100,000	2 824 229 408 · 10 ^{45 6573}
1,000,000	8,263,931,688 · 10 ^5,565,708

電卓を使った数値の階乗

前の例でわかるように、連続する 2 つの数値の階乗の結果は指数関数的に増加するため、大きな数値の階乗を知ることは非常に困難です。そこで、電卓を使って数値の階乗を求める方法を説明します。

関数電卓にはx という記号のキーがあります。とか、ん！整数の階乗を計算するために使用されます。したがって、階乗の価値を判断するには、電卓で次の手順を実行する必要があります。

$n! \quad \color{red} \bm{\longrightarrow} \quad \color{black} n\rightarrow \boxed{x!} \rightarrow \boxed{=}$

通常、CASIO 電卓には階乗キー x! が付いています。とか、ん！ x ^-1ボタンの上。

例として、計算機を使用して階乗を解くので、解き方を知っているかどうかを確認できます。たとえば、9 の階乗を実行します。

$9! \quad \color{red} \bm{\longrightarrow} \quad \color{black} 9\rightarrow \boxed{x!} \rightarrow \boxed{=} \rightarrow 362880$

9 の階乗を求めるには、まず数値 9 を入力し、次にキーを押す必要があります。

$\boxed{x!}$

最後にイコールボタンを押します。この場合、計算機は 362,880 という結果を表示するはずです。

階乗数の応用

数値の階乗関数は非常に単純でばかげた演算のように思えるかもしれませんが、高度な代数ではかなり頻繁に使用されます。次に、階乗の主な用途を見ていきます。

まず、階乗は組み合わせ数を計算するために不可欠な演算であり、特別な演算ではありません。組み合わせ数が何であるかわからない場合は、このリンクで組み合わせ数が何で構成され、どのように計算されるかを確認できます。ここには、例、解決された演習、およびその特性が記載されています。さらに、実際のアプリケーションが多数あるため、それが何に使用されているかを確認することができます。

階乗は、関数のテイラー多項式を決定するために数学でも使用されます。

同様に、階乗は特定の組み合わせ問題を解決するために、特に組み合わせと順列を計算するために使用されます。この意味で、階乗は、組み合わせ論を使用して確率を計算するためにもよく使用されます。

n 個の要素の順列は、これらの要素で作成できるさまざまな配置のそれぞれに対応します。したがって、順列を計算するには階乗が使用されます。たとえば、問題で 7 つのオブジェクトが配置される可能性の数を見つけたい場合は、7 の階乗を計算する必要があります。

次に、解決された演習を見てみましょう。

5足の靴がありますが、アレンジは何通りあるでしょうか？

この演習では、これら 5 足の靴を履く順序を考慮して組み合わせるすべての可能な方法を発見する必要があります。したがって、問題を解決するには、5 の階乗を計算するだけです。

$5! = 1\cdot 2 \cdot 3\cdot 4\cdot 5 =120$

つまり、5足の靴を120通りの配置ができるということです。

階乗数の性質

階乗数には次の特徴があります。

nがmより大きい 2 つの正の整数nおよびmである場合、明らかにnの階乗の値はmの階乗の値より大きくなります。

$n>m \quad \longrightarrow \quad n! > m!” title=”Rendered by QuickLaTeX.com” height=”15″ width=”183″ style=”vertical-align: -2px;”> <ul style=$

数値の階乗は、因数の 1 つがより小さい数値の階乗になるように階乗分解できます。

$n>m \quad \longrightarrow \quad n!= n\cdot (n-1) \cdots (m+1)\cdot m!” title=”Rendered by QuickLaTeX.com” height=”19″ width=”361″ style=”vertical-align: -5px;”> たとえば、6 は 4 より大きいため、6 の階乗の式は次のように簡略化できます。 <p class=$ $6! = 6 \cdot 5 \cdot 4!$

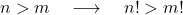
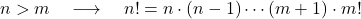
次の代数式は、1 の階乗を除く任意の数値の階乗に有効です。

$\displaystyle n!< \left( \frac{n+1}{2} \right)^n$

負または 10 進数の階乗

正の整数の階乗の値を求める方法を説明しましたが、負の数や 10 進数の階乗を計算することはできるでしょうか?答えは「はい」ですが、高度な数学の知識が必要です。

負の数と 10 進数の階乗は、オイラーの「ガンマ関数」と呼ばれる特別な関数を使用して計算されます。この関数は、次の積分で定義されます。

$\displaystyle \Gamma(z)=\int_0^\infty t^{z-1} e^{-t}\, \mathrm{d}t$

したがって、次の方程式が常に真であるため、ガンマ関数を使用して任意のタイプの階乗を解くことができます。

$n! = \Gamma(n+1)$

したがって、たとえば 0.5 の階乗を見つけるには、次の値を見つける必要があります。

$\Gamma(1,5)$

なぜなら：

$0,5! = \Gamma(0,5+1) =\Gamma(1,5)$

そして積分の解は0.5の階乗に相当します。

明らかに、ガンマ関数の積分を解くのは簡単ではありません。多くの数学的概念を事前に説明する必要があるため、この記事では説明しません。ただし、負の数または 10 進数の階乗を計算できる可能性があることを知っておいてください。

実際、例として、いくつかの負の階乗値と 10 進値を計算しました。

$\underline{\bm{n}}$	$\underline{\bm{n!}}$
$\displaystyle \left(\frac{1}{2}\right)!$	$\displaystyle \frac{1}{2}\sqrt{\pi}$
$\displaystyle \left(-\frac{1}{2}\right)!$	$\displaystyle \sqrt{\pi}$
$\displaystyle \left(\frac{3}{2}\right)!$	$\displaystyle \frac{3}{4}\sqrt{\pi}$
$\displaystyle \left(\frac{5}{2}\right)!$	$\displaystyle \frac{15}{8}\sqrt{\pi}$