▷ 共通因数を取り除く（または抽出する）方法✅（解決済み演習）

このページでは、多項式の共通約数の取り方（抽出）について説明します。ここでは、さまざまな種類の共通因数が見つかり、これがどのように達成されるかのいくつかの例を見ることができます。さらに、段階的に解決される演習でトレーニングすることもできます。

共通因数は何ですか?

数学では、共通因数は多項式のすべての項に存在する因数です。つまり、共通因数は多項式の各項を乗算する数値または文字で構成されます。

例として、次の多項式の共通因数を特定します。

$4x+4y$

4 番目では、多項式のすべての項で繰り返されます。

$\color{red} \bm{4} \color{black} x + \color{red} \bm{4} \color{black} y$

したがって、この多項式の共通因数は 4 に等しくなります。

$\displaystyle \text{Factor com\'un} = 4 {\phantom{\frac{1}{2}}$

共通因数を取得 (または抽出) する方法

共通因数の意味がわかったら、多項式から共通因数を求める方法を見てみましょう。

多項式の 2 つ以上の項に共通因数がある場合、その共通因数を取得 (または抽出) して、多項式の加算または減算を乗算に変換できます。

これを書くのは少し難しいように思えるかもしれないので、例を使って多項式から共通因数を抽出する方法を見てみましょう。

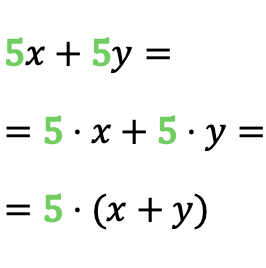
例でわかるように、数値 5 は単項式 5x と単項式 5y で繰り返されているため、多項式の共通因数は 5 です。したがって、共通因数を特定したら、単項式の合計を次のように変換できます。製品。

共通因数はすべての加数を乗算する必要があるため、共通因数を抽出するときは括弧を入れることを忘れないでください。

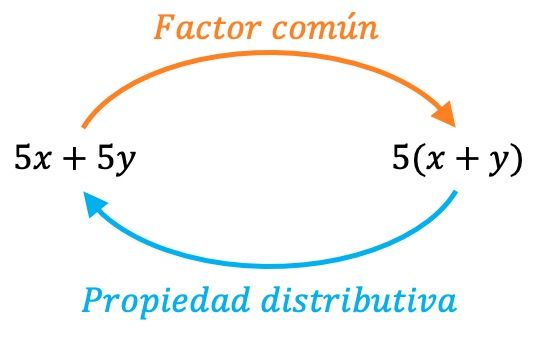
共通因数の除去は、分配特性の逆の操作です。つまり、実際には分配特性を逆に適用しています。したがって、逆のプロセスを実行することで、共通因数が正しく抽出されたことを常に検証できます。

分配特性を適用して最初から同じ多項式が得られた場合、これは共通因数が正しく得られたことを意味します。
一方、分配性質を利用した結果が元の多項式とは異なる多項式になった場合、それは共通因数を抽出する過程でミスがあったことを意味します。

共通因数の取得 (または抽出) の例

共通因数の概念を理解するために、さらに多くの例を示します。

例1

この例でわかるように、共通因数は 3 つ以上の項から同時に抽出できます。

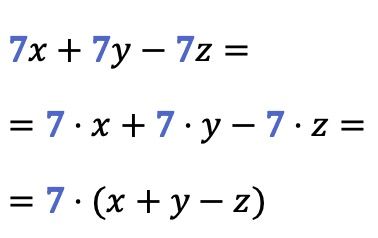
例 2

変数 (または文字) から共通因子を抽出することもできます。

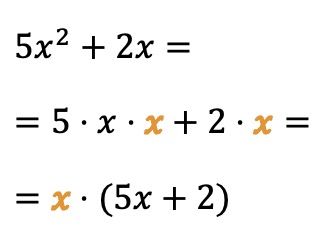
この場合、文字 x は多項式の 2 つの項を乗算するため、変数 x を共通因数として取ることで代数式を簡素化できます。

例 3

この例では、最初の項には変数 x の 3 乗があり、第 2 項では x の 2 乗があるため、両方の項に 2 つの x があります。したがって、共通因数は単なる x ではなく、 x ²になります。

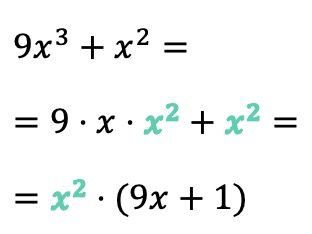
一方、多項式の共通因数が項と正確に一致する場合、共通因数を抽出するときに、その場所に 1 を置く必要があることに注意してください。そうでなければ、その場所に何も配置しなければ、同等の式は得られません。

例 4

場合によっては、共通因数がそれほど明白ではなく、直接目に見えない場合もありますが、むしろ単項式の係数の約数です。たとえば、6 と 9 の階乗分解には 3 が含まれるため、次の例の共通因数は 3 です。

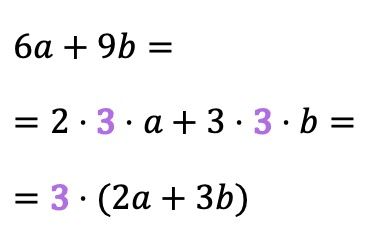
このタイプの共通因数は、代数学の書籍によっては最大公約数と呼ばれています。これは、共通因数が多項式項の係数の最大公約数 (GCD) でもあるためです。

ここまで読んだということは、多項式の共通因数を求める方法をすでに知っていることを意味します。しかし、その共通因数が何なのか疑問に思ったことはありませんか?共通因数の応用例の 1 つは、多項式の因数分解に使用されることです。まだそれが何であるかわからない場合は、このリンクで、多項式因数分解とは何なのか、そしてこの多項式演算を実行するために共通因数がなぜ非常に重要であるのかを確認できます。

分数の公約数

共通因数は、分子と分母に多項式を使用して項を分数に単純化する場合にも非常に役立ちます。

これがどのように行われるかを確認するために、例として次の分数を単純化してみましょう。

$\cfrac{2x^2+4}{14x+8y}$

最初に行う必要があるのは、分子多項式と分母多項式の公約数を見つけることです。この場合、2 つの多項式の公約数は 2 です。

$\cfrac{\color{red} \bm{2} \color{black}\cdot x^2+\color{red} \bm{2} \color{black}\cdot 2 }{\color{red} \bm{2} \color{black}\cdot 7x+\color{red} \bm{2} \color{black} \cdot 4y}$

次に、2 つの多項式の共通因数を抽出しましょう。

$\cfrac{\color{red} \bm{2} \color{black}\left(x^2+2\right)}{\color{red} \bm{2} \color{black}\left(7x+4y\right)}$

両方の多項式の共通因数を取得したら、分子と分母で繰り返される因数を削除する必要があります。

$\cfrac{\cancel{2}\left(x^2+2\right)}{ \cancel{2}\left(7x+4y\right)}$

結論として、簡略化された分数は次のようになります。

$\cfrac{x^2+2}{7x+4y}$

グループ分けによる共通因数

多項式の項を減らす 1 つの方法は、項をグループ化することによる共通因数法を使用することです。これは二重共通因数抽出とも呼ばれます。その名前が示すように、この手順は多項式の項を 2 回グループ化することで多項式の式を簡略化することで構成されます。

この方法は少し複雑なので、次の多項式を使用して段階的にどのように適用されるかを見てみましょう。

$x^2+2x+5x+10$

まず、考えられる 2 つの異なる共通因数を決定する必要があるため、多項式を 2 つの部分に分割します。

$(x^2+2x)+(5x+10)$

この場合、要素 x ²と 2x は共通因数として文字 x を持ち、項 5x と 10 は共通因数として 5 を持ちます (10 は 5 の倍数であるため)。したがって、次の 2 つの要素が共通しています。

$(x\cdot x+2\cdot x)+(5\cdot x+5\cdot 2)$

$x(x+2)+5(x+2)$

そして最後に、残りの 2 つの多項式積には因数 (x+2) があるため、次のように多項式を単純化できます。

$(x+2)\cdot (x+5)$

ご覧のとおり、この方法は決して簡単ではありません。コメントでご質問がございましたら、お気軽にお問い合わせください。できるだけ早くお答えいたします。

共通因数演習を段階的に解決

多項式から共通因数を抽出する練習ができるように、いくつかの演習を段階的に解決していきます。

演習 1

次の多項式から共通因数を抽出します。

$\text{A)} \ 6a+6b$

$\text{B)} \ 3x^2+8x$

$\text{C)} \ 2x-4$

$\text{D)} \ -5x^4+x^2$

解決策を見る

A)最初の多項式を構成するすべての項には 6 が含まれるため、多項式の共通因数は 6 になります。

$6a+6b = 6\cdot a + 6 \cdot b = \bm{6\cdot (a+b)}$

B) 2 番目の多項式では、そのすべての要素に少なくとも 1 つの文字 x が含まれます。多項式の共通因数は次のとおりです。

$3x^2+8x = 3x \cdot x+8\cdot x= \bm{x\cdot (3x+8)}$

C)多項式の最初の単項式は明らかに 2 であり、2 番目の単項式は 2 の倍数です。したがって、多項式の共通因数は 2 です。

$2x-4= 2\cdot x - 2\cdot 2 =\bm{2\cdot (x-2)}$

D)最後の多項式では、すべての変数が少なくとも 2 乗されます。したがって、共通因数は x ²になります。

$-5x^4+x^2= -5x^2\cdot x^2 +1 \cdot x^2 = \bm{x^2\cdot (-5x^2+1)}$

共通因数が項と同じである場合は、その位置に 1 を置く必要があることに注意してください。

演習 2

次の多項式の共通因数を考えてみましょう。

$\text{A)} \ 8x^2 + 10y^3$

$\text{B)} \ 5x^3-2x^2+4x$

$\text{C)} \ 25x^5+15x^3-20$

$\text{D)} \ 9x^4-3x^3-21x^2-6x$

解決策を見る

A)最初の多項式を構成する要素の係数はすべて 2 の倍数であるため、共通因数を抽出すると、多項式は次のようになります。

$\begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}$

B)多項式のすべての項において、少なくとも 1 つの x が存在するため、次のようになります。

$\begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}$

C)多項式のすべての項の係数の最大公約数は 5 であるため、上記多項式の公約数は 5 になります。

$\begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}$

D)多項式のすべての項には少なくとも 1 つの x があり、さらにすべての係数は 3 の倍数です。したがって、多項式の共通因数は 3x です。

$\begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}$

演習 3

次の各多項式の共通因数を見つけて減算します。

$\text{A)} \ 4a^2b^5+7a^4b^3-10a^6b^4$

$\text{B)} \ 16x^4y^7z+8x^2y^2z^2+ 24x^3y^5$

$\text{C)} \ 6ab^2c^4-6ab^2c+12a^3b^2c$

$\text{D)} \ 18x^2y+10xy-5xy^3+4z$

解決策を見る

A)すべての単項式には少なくとも次の文字が含まれます。

$a$

四角と文字

$b$

3 乗なので、共通因数は次のようになります。

$a^2b^3:$

$\begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}$

B)多項式の係数はすべて 8 の倍数であり、さらに、リテラル部分として少なくとも x ²と y ²を持ちます。したがって、多項式の共通因数は 8x ² y ²です。

$\begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}$

C)この場合、共通因数は中間単項式の値と一致します。

$\left(6ab^2c\right)$

、他の単項式の係数は次の倍数であるため、

$6$

そして絶対に誰もが持っています

$ab^2c:$

$\begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}$

D)この特定のケースでは、多項式のすべての項で繰り返される因数がないため、多項式には共通因数がありません。したがって、多項式を代数的に簡略化することはできません。

$18x^2y+10xy-5xy^3+4z$

演習 4

共通因数を使用して、次の代数分数を簡略化します。

$\text{A)} \ \cfrac{10x^2+30}{5x-20}$

$\text{B)} \ \cfrac{16x^2-8}{24x-32}$

$\text{C)} \ \cfrac{49x^3+7x}{35x^2-14}$

$\text{D)} \ \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}$

解決策を見る

代数的な分数、つまり多項式を含む分数を簡略化する手順は、分数の分子と分母から共通約数を抽出し、上下に繰り返される約数を削除します。分数の下。それで：

$\text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}$

$\text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}$

$\text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}$

$\text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}$

演習 5

次の多項式の共通因数を計算します。

$\text{A)} \ \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}$

$\text{B)} \ \sqrt{12x^3+16}$

$\text{C)} \ x^2+4x-3x-12$

$\text{D)} \ \cfrac{3}{4}x^2+ \cfrac{1}{2}x-\cfrac{5}{6}$

解決策を見る

A)多項式のすべての項は 3 番目まで階乗分解できるため、次のようになります。

$\begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}$

B)ルート内の多項式の共通因数は 4 ですが、平方根を計算することで共通因数を出力できます。

$\begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}$

C)この多項式では、グループ化によって共通因数を抽出するプロセスを適用できます。

$\begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}$

D)多項式の小数係数はすべて 2 の倍数であるため、多項式の公約数は 1/2 です。

$\begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}$

👇👇👇 この説明についてどう思いましたか?気に入りましたか？また、多項式の共通因数の求め方について質問がある場合、または演習が理解できない場合は、いつでもコメント欄で質問していただければお答えいたします。 👇👇👇

共通因数を抽出または削除します

共通因数は何ですか?

共通因数を取得 (または抽出) する方法

共通因数の取得 (または抽出) の例

例1

例 2

例 3

例 4

分数の公約数

グループ分けによる共通因数

共通因数演習を段階的に解決

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする返信をキャンセル

共通因数は何ですか?

共通因数を取得 (または抽出) する方法

共通因数の取得 (または抽出) の例

例1

例 2

例 3

例 4

分数の公約数

グループ分けによる共通因数

共通因数演習を段階的に解決

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

コメントする返信をキャンセル