平面の暗黙的、一般またはデカルト方程式

一般方程式またはデカルト方程式とも呼ばれる、暗黙的な平面方程式 (公式) の計算方法の説明。さらに、法線ベクトルから平面の方程式を見つける方法もわかります。さらに、例題や演習を段階的に解くことができます。

計画の暗黙的な方程式または一般方程式は何ですか?

解析幾何学では、平面の暗黙方程式(平面の一般方程式またはデカルト方程式とも呼ばれます) は、任意の平面を数学的に表現できる方程式です。平面の陰的方程式または一般方程式を求めるには、その平面に属する 1 つの点と 2 つの線形独立ベクトルが必要です。

計画の陰的方程式または一般方程式の式

点と平面の 2 つの方向ベクトルを考えてみましょう。

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

平面の陰的な一般方程式またはデカルト方程式は、次の行列式を解き、結果を 0 に設定することによって取得されます。

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

したがって、結果として得られる計画の暗黙的な方程式または一般方程式は次のようになります。

$Ax+By+Cz+D=0$

式内の 2 つのベクトルが互いに線形独立していることが重要です。つまり、それらのベクトルは異なる方向を持っている必要があります。そして、この条件が満たされるには、2 つのベクトルが平行でないだけで十分です。

この式の理由を知る必要はありませんが、以下でそのデモンストレーションをご覧ください。

計画のパラメトリック方程式から始めて、計画の暗黙的 (または一般) 方程式に進みます。

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

まず、各パラメトリック方程式の独立項を方程式の反対側に渡します。

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

または同等のもの:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

上記の方程式系が実行可能な解を得るには、次の行列のランクが 2 に等しくなければなりません (ルーシュ-フロベニウスの定理)。

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

したがって、前の行列の範囲が 2 でなければならない場合、3×3 行列式は必ずゼロに等しくなければなりません。

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

そして、この行列式を解くことによって、平面の一般的な陰的方程式またはデカルト方程式が得られます。

$Ax+By+Cz+D=0$

ここまで、平面の陰的 (または一般) 方程式とパラメトリック方程式を見てきましたが、ベクトル方程式や正準方程式など、平面を解析的に表現する方法はさらにたくさんあります。このリンクでは、計画内のすべての方程式の公式と説明をご覧いただけます。

平面の陰的方程式または一般方程式を見つける方法の例

例を通して、平面の暗黙的な (または一般またはデカルト) 方程式を決定する方法を見てみましょう。

点を通過する平面の陰的方程式または一般方程式を求めます。
$P(3,1,-1)$

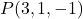
ベクトルが含まれています

$\vv{\text{u}}=(2,0,3)$

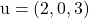
そして

$\vv{\text{v}}=(4,-1,2).$

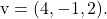
平面の一般方程式または陰的方程式を計算するには、2 つのベクトル、変数、点の座標によって形成される次の行列式を解く必要があります。

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

したがって、ベクトルと点を式に代入します。

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

次に、次数 3 の行列式を、たとえば、Sarrus ルールまたは余因子 (または代理) を使用して解決します。

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

次に、用語を操作してグループ化します。

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

したがって、計画の暗黙的または一般方程式は次のようになります。

$\bm{3x+8y-2z-19 = 0}$

法線ベクトルから平面の暗黙的な方程式または一般方程式を計算します。

平面の方程式における非常に典型的な問題は、点とその法線 (または垂直) ベクトルを考慮して、特定の平面の方程式がどのように見えるかを見つけることです。それでは、どのように機能するかを見てみましょう。

ただし、平面に垂直なベクトルの成分 X、Y、Z がそれぞれ、当該平面の陰的な (または一般的な) 方程式の係数 A、B、C と一致することを最初に知っておく必要があります。

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

金

$\vv{n}$

平面に直交するベクトルです

$\pi.$

前の関係がわかったら、このタイプの平面方程式の問題を解く例を見てみましょう。

点を通過する平面の陰的な方程式または一般方程式を決定します。
$P(1,0,-2)$

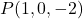
その法線ベクトルの 1 つは、

$\vv{n}=(3,-1,2) .$

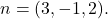
平面の陰的な一般方程式またはデカルト方程式の式は次のとおりです。

$Ax+By+Cz+D=0$

したがって、法線ベクトルから係数 A、B、C を見つけることができます。これらは法線ベクトルの成分に等しいためです。

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

パラメーター D を見つける必要があるだけです。これを行うには、平面に属する点の座標を方程式に代入します。

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

したがって、計画の暗黙的または一般方程式は次のようになります。

$\bm{3x-y+2z+1 = 0}$

平面の陰的方程式または一般方程式の解決済み問題

演習 1

点を通過する平面の陰的方程式または一般方程式を求めます。

$P(-2,1,3)$

ベクトルが含まれています

$\vv{\text{u}}=(4,1,3)$

そして

$\vv{\text{v}}=(5,3,-1).$

解決策を参照

平面の一般方程式または陰的方程式を計算するには、2 つのベクトル、3 つの変数、および点の座標によって形成される次の行列式を解く必要があります。

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

したがって、ベクトルと点を式に代入します。

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

次に、選択した方法で 3×3 行列の行列式を解きます。

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

最後に、操作を実行して、類似した用語をグループ化します。

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

したがって、計画の暗黙的または一般方程式は次のようになります。

$\bm{-8x+11y+7z-20 = 0}$

演習 2

ポイントかどうかを判断する

$P(-1,5,-3)$

以下のプランに属します。

$\pi : \ 2x+y+6z-5=0$

解決策を参照

点が平面上にあるためには、その方程式を検証する必要があります。したがって、点のデカルト座標を平面の方程式に代入し、方程式が満たされるかどうかを確認する必要があります。

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

点は平面の方程式を尊重しないため、この平面の一部ではありません。

演習 3

次の 3 つの点を含む計画の暗黙的な (または一般的な) 方程式を見つけます。

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

解決策を参照

平面の暗黙的な方程式を見つけるには、平面内で結合する 2 つの線形に独立したベクトルを見つける必要があります。そして、このために、3 つの点によって定義される 2 つのベクトルを計算できます。

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

見つかった 2 つのベクトルの座標は比例していないため、実質的に互いに線形独立しています。

これで、平面の 2 つの方向ベクトルと 1 つの点がすでにわかっているので、平面の一般方程式の公式をすでに適用できます。

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

ベクトルと 3 つの点の 1 つを式に代入します。

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$