平面のパラメトリック方程式

このページでは、計画のパラメトリック方程式が何であるか、およびそれらがどのように計算されるか (式) がわかります。さらに、例を見て、段階的に解決される演習で練習することができます。

平面のパラメトリック方程式とは何ですか?

解析幾何学では、平面のパラメトリック方程式は、任意の平面を数学的に表現できる方程式です。平面のパラメトリック方程式を見つけるには、その平面に属する 1 つの点と 2 つの線形独立ベクトルのみが必要です。

計画のパラメトリック方程式の定式化

点と平面の 2 つの方向ベクトルを考えてみましょう。

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

平面のパラメトリック方程式の公式は次のとおりです。

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

金

$\lambda$

そして

$\mu$

は 2 つのスカラー、つまり 2 つの実数です。

平面方程式の 2 つの方向ベクトルが線形に独立していること、つまり、異なる (非平行な) 方向を持つことが重要です。そうでない場合、上記の式は計画を示さないことになります。

一方、パラメトリック方程式とは別に、一般平面方程式など、空間 (R3) 内の平面を解析的に表現する他の方法があることに留意してください。このリンクでは、その公式、計画のパラメトリック方程式から計算される方法、例、および解決された演習が見つかります。

平面のパラメトリック方程式を見つける方法の例

平面のパラメトリック方程式が何であるかを理解したら、例を使用してそれがどのように計算されるかを見てみましょう。

点を通過する平面のパラメトリック方程式を求めます。
$P(1,3,2)$

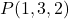
ベクトルが含まれています

$\vv{\text{u}}=(2,0,-1)$

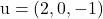
そして

$\vv{\text{v}}=(4,2,3)$

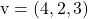
計画のパラメトリック方程式を決定するには、その式を適用するだけです。

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

そして、点と各方向ベクトルを方程式に代入します。

$\displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}$

平面のベクトル方程式からパラメトリック方程式に移行する方法

平面のパラメトリック方程式を決定する別の方法は、平面のベクトル方程式から行うものです。以下でデモをご覧いただけます。

任意の平面のベクトル方程式を次のようにします。

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

まずベクトルとスカラーの積を演算して実行します。

$(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)$

次に、コンポーネントを追加します。

$(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)$

そして最後に、各変数に対応する座標を個別に同化することで、平面のパラメトリック方程式を取得します。

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

上の 2 つの例からわかるように、平面のパラメトリック方程式を見つけるのは比較的簡単です。ただし、問題は少し複雑になる可能性があるため、以下にさまざまな難易度の解決済み演習をいくつか用意して練習してください。

平面のパラメトリック方程式の問題を解決しました

演習 1

ベクトルを含む平面のパラメトリック方程式を決定します。

$\vv{\text{u}}=(2,1,5)$

そして次の 2 つのポイントを通過します。

$A(3,2,-1)$

そして

$B(-2,-1,1).$

解決策を参照

平面の方程式を知るには、1 つの点と 2 つのベクトルが必要ですが、この場合はベクトルが 1 つしかないため、平面の別の方向ベクトルを見つける必要があります。これを行うには、平面の 2 点を定義するベクトルを計算します。

$\vv{AB} = B - A = (-2,-1,1) - (3,2,-1) = (-5,-3,2)$

平面と点の 2 つの方向ベクトルがすでにわかっているので、平面のパラメトリック方程式の公式を使用します。

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

そして、2 つのベクトルと平面上の 2 つの点の 1 つを方程式に代入します。

$\displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}$

$\displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}$

演習 2

次の 3 つの点を含む平面のパラメトリック方程式を求めます。

$A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)$

解決策を参照

平面のパラメトリック方程式を見つけるには、平面内でリンクする 2 つの線形独立ベクトルを見つける必要があります。そして、このために、3 つの点によって定義される 2 つのベクトルを計算できます。

$\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)$

$\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)$

見つかった 2 つのベクトルの座標は比例していないため、互いに線形独立しています。

2 つの方向ベクトルと平面上の点がすでにわかっているので、平面のパラメトリック方程式の公式を適用します。

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

そして、2 つのベクトルと平面の 3 つの点の 1 つを方程式に代入します。

$\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}$

$\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}$

演習 3

次のベクトル方程式で定義される平面のパラメトリック方程式を計算します。

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

解決策を参照

平面のベクトル方程式をパラメトリック方程式に変換するには、座標を操作してから各変数を個別に解く必要があります。

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

$(x,y,z)=(0,-1,5)+(6\lambda,\lambda,-2\lambda) + (\mu,-\mu,3\mu)$

$(x,y,z)=(6\lambda+\mu,-1+\lambda-\mu,5-2\lambda+3\mu)$

$\displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}$

演習 4

直線を含む平面のパラメトリック方程式を求めます。

$r$

そして右側に平行です

$s.$

次の行になります:

$\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}$

解決策を参照

平面のパラメトリック方程式を見つけるには、2 つの方向ベクトルと平面上の点を知る必要があります。命令には次の行が含まれていることがわかります

$r$

したがって、方向ベクトルとこの線上の点を取得して平面を定義できます。さらに、このステートメントは、平面が直線に平行であることを示しています。

$s,$

したがって、この直線の方向ベクトルを平面方程式に使用することもできます。

権利

$r$

はパラメトリック方程式の形式で表現されるため、その方向ベクトルの成分はパラメータ項の係数になります。

$t:$

$\vv{r} =(1,-3,2)$

そして、これと同じ線上の点のデカルト座標は、パラメトリック方程式の独立項です。

$P(1,2,4)$

一方、直線は、

$s$

は連続方程式の形式であり、その方向ベクトルの成分が分数の分母になります。

$\vv{s} =(2,2,-3)$

したがって、計画のパラメトリック方程式は次のようになります。

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

$\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}$

平面のパラメトリック方程式とは何ですか?

計画のパラメトリック方程式の定式化

平面のパラメトリック方程式を見つける方法の例

平面のベクトル方程式からパラメトリック方程式に移行する方法

平面のパラメトリック方程式の問題を解決しました

演習 1

演習 2

演習 3

演習 4

コメントする 返信をキャンセル

コメントする返信をキャンセル