ここでは、平行線の意味、2 本の線が平行かどうかを判断する方法、そのプロパティなど、平行線に関するすべてがわかります。さらに、平行線のいくつかの例と解答済みの演習を見ることができます。
平行線とは何ですか?
平行線とは、決して交わらない線、つまり、たとえ軌道が無限に伸びても決して接触しない線のことです。したがって、2 本の平行線の点は常に同じ距離にあり、さらに 2 本の平行線には共通点がありません。
たとえば、次の 2 つの直線は平行です。

一般に、2 本の線が 2 本の垂直バーと平行であることを示します ||行間
一方、2 本の平行線は決して交差しないという事実にもかかわらず、解析幾何学では、それらは同じ方向を持っているため、角度 0 度を形成すると言います。
2本の線が平行になるのはどんなとき?
平行線の定義を理解したら、2 本の平行線を見つける方法を見てみましょう。もちろん、線をグラフにしてグラフ上で交差するかどうかを確認するのも 1 つの方法ですが、さらにシンプルで使いやすい方法があります。
2 本の直線の平行度をその傾きで決定します。
2 本の線が平行かどうかは、各線の傾きを見ることでわかります。線の傾きがパラメータであることを忘れないでください。
![]()
陽的な方程式と直線の点と傾きの方程式から次のようになります。
![]()
ただし、線の傾きを決定する方法はいくつかあるため、計算方法を知るには、線の傾きの公式を参照することをお勧めします。さらに、リンク先のページには、線の傾きが何を表すのか、そしてなぜそれが線にとってそれほど重要なのかについての説明もあります。
したがって、平面内で、 2 つの直線が同じ傾き(係数 m)で原点での異なる縦座標(係数 n) を持っている場合、2 つの直線は平行です。
たとえば、次の 2 つの直線は平行です。
![]()
両方とも同じ傾きを持ち、さらに独立項が異なるため、これらは 2 本の平行線です。
![]()
![]()
2 つのラインが同じ傾きを持ち、同時に原点に同じコンピューターがある場合、それらはまったく同一であるため、それらは同一のラインになることに注意してください。
陰的な方程式から 2 つの直線の平行度を求める
この直線の暗黙的な (または一般的な) 方程式は次のとおりであることに注意してください。
![]()
したがって、 2 つの直線の係数 A と B が互いに比例するが、係数 C には比例しない場合、これは直線が平行であることを意味します。
![]()
![]()
一般的な (または暗黙的な) 方程式形式で表現された 2 本の平行線を次に示します。
![]()
変数の前に数字があるため、これらは並列です。
![]()
変数の前の数字に比例します
![]()
ただし、独立した用語ではありません。
![]()
前と同様に、2 つの暗黙的な直線のすべての係数 (A、B、および C) が比例する場合、これは 2 つの直線が一致する、言い換えればそれらが等しいことを意味します。
平行線の性質
平行線の特徴は次のとおりです。
- 対称性: 1 つの線が別の線に平行な場合、この線も最初の線と平行になります。この性質は垂線にもあります。
![]()
- 推移的プロパティ: 線が別の線と平行で、この 2 番目の線が 3 番目の線と平行である場合、最初の線も 3 番目の線と平行になります。
![Rendered by QuickLaTeX.com \left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q](https://mathority.org/wp-content/ql-cache/quicklatex.com-d8ed30d043440defc6ebfd30c740e937_l3.png)
- 2 本の平行な直線の方向ベクトル (直線の方向を示すベクトル) のスカラー積は、それらの加群の積に等しくなります。
![]()
- さらに、2 本の平行線の方向ベクトルは比例するため、常に互いに線形に依存します。
この条件は線が平行であるためには必要ですが、十分ではありません。つまり、2 本の平行な線は比例した方向ベクトルを持つ必要がありますが、2 本の線が比例した方向ベクトルを持つという事実は、それらが平行であることを直接意味するわけではありません。一致する線も比例した方向ベクトルを持ちます。
- 横軸 (X 軸) に平行な線は水平であり、常に次の形式になります。

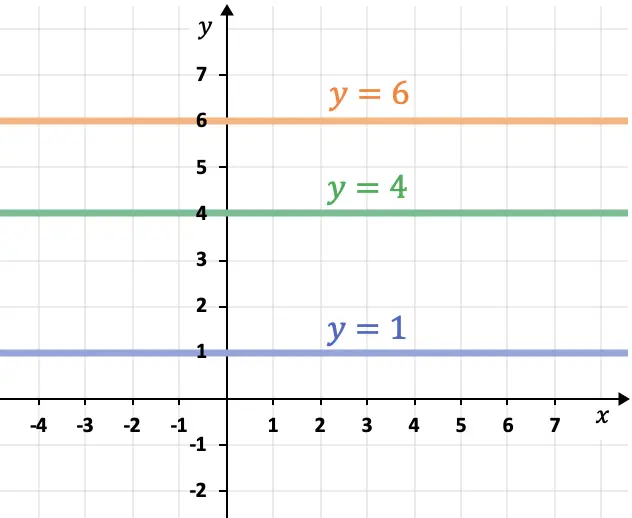
- コンピュータの軸 (Y 軸) に平行な線は垂直であり、常に式に従います。

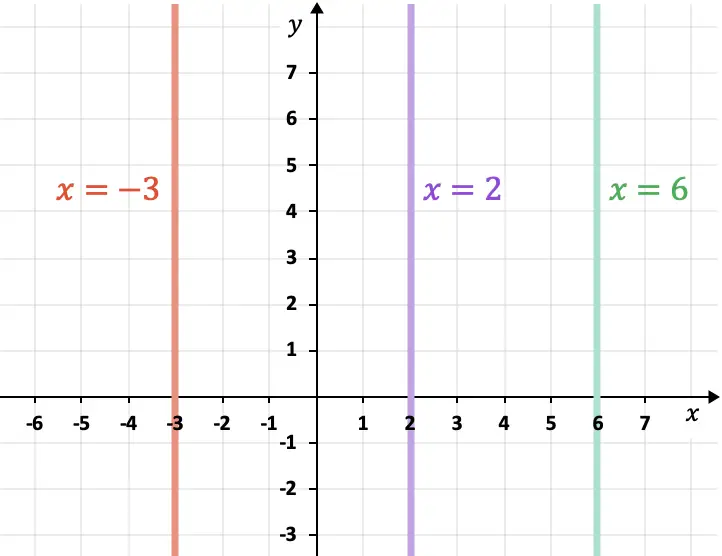
平面内の 2 本の平行線の間の距離を計算する方法
平面 (R2) 内の 2 本の平行線の間の距離を求めるには、2 本の線のうちの 1 つ上の点を取得し、この点からもう 1 つの線までの距離を計算するだけです。
2 本の平行線は常に同じ距離離れているため、このように行うことができます。

一方、この式を使用したときに距離が 0 単位になった場合、これは線がある点で互いに接触しており、したがって線が平行ではなく交差、一致、または直交していることを意味します。必要に応じて、このタイプのラインの違いを当社の Web サイトで確認できます。
したがって、これがどのように行われるかを理解できるように、例として次の 2 本の平行線の間の距離を決定します。
![]()
最初に行う必要があるのは、線の 1 つ (目的の線) 上で点を取得することです。この場合、線上の点を計算します。
![]()
これを行うには、変数の 1 つに値を与える必要があります。たとえば、次のようにします。
![]()
![]()
そして今、他の変数をクリアします(
![]()
) この時点での価値を知るために得られた方程式:
![]()
![]()
![]()
したがって、直線から得られる点は、
![]()
東:
![]()
そして、すでに線上に点があれば、点から線までの距離の公式を使用して、その点から他の線までの距離を計算します。
![]()
![]()
したがって、2 本の平行線間の距離は 0.45 単位に相当します。
平行線で解決された問題
演習 1
次の線のうち平行なものはどれですか?
![Rendered by QuickLaTeX.com \begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1baec7cae9d15180df86f9cf4f44d828_l3.png)
2 本の直線の傾きが同じ (切片が異なる) 場合、その直線は平行です。したがって、各直線の傾きは次のようになります。
![]()
![]()
![]()
![]()
つまり線だけが平行になります
![]()
そして
![]()
それらは等しい傾きを持つ唯一のものだからです。
演習 2
直線に平行な直線の明示的な方程式を求めます。
![]()
そしてその点で何が起こるか
![]()
まっすぐであること
![]()
![]()
線が線と平行になるように
![]()
両方とも同じ傾きを持つ必要があります。そして線の傾き
![]()
は 3:
![]()
したがって、見つける必要がある直線の明示的な方程式は次のようになります。
![]()
線の傾きがわかったら、その線に属する点を線の方程式に代入して切片を計算できます。
![]()
![]()
![]()
![]()
したがって、この直線の明示的な方程式は次のようになります。
![]()
演習 3
未知数の値を計算する
![]()
そして
![]()
次の 2 つの線が平行になるようにします。
![]()
線は一般的な (または暗黙的な) 方程式形式で記述されます。したがって、2 つの直線が平行であるためには、それらの係数 A と B が比例する必要があります。つまり、次の方程式が満たされる必要があります。
![]()
したがって、未知の値を取得するには、前の式を解く必要があります。
![]()
これを行うには、分数を横方向に乗算します。
![]()
![]()
![]()
一方、線が平行であるためには、その独立項が他の係数に比例することはありません。
![]()
したがって、前と同様に、分数を横に乗算して不等式を解決します。
![]()
![]()
![]()
つまり、2本の直線が平行になるように、
![]()
2でなければなりません、そして
![]()
3 を除く任意の実数を指定できます。
演習 4
次の 2 本の平行線の間の距離はいくらですか?
![]()
まず、これらが 2 本の平行線であることを確認します。このため、変数の係数は
![]()
そして
![]()
相互に比例する必要がありますが、独立した項には比例しません。
![]()
確かに、線は平行なので、この手順を適用できます。
次に、線の 1 つ (必要な線) から点を取得する必要があります。この場合、線上の点を計算します。
![]()
これを行うには、変数の 1 つに値を割り当てる必要があります。たとえば、次のようにします。
![]()
![]()
そして今、他の変数をクリアします(
![]()
) この時点での値を知るために得られた方程式の次のとおりです。
![]()
![]()
![]()
したがって、直線から得られる点は
![]()
東:
![]()
線上の点がわかったら、次の式を使用してその点から他の線までの距離を計算します。
![]()
![]()