このページでは、平行四辺形の法則について説明します。さらに、平行四辺形の法則を使用したベクトルの加算と減算の例と、実際の応用例をいくつか示します。
平行四辺形の法則とは何ですか?
すでにご存知のとおり、ベクトル量には 2 つの成分 (R2) または 3 つの成分 (R3) があり、ベクトルは異なる方向を持つ可能性があるため、実数と同じ方法で加算または減算することはできません。したがって、ベクトル演算を実行するには、次の要素からなる平行四辺形規則などの他のメソッドが必要です。
数学では、平行四辺形の法則は、グラフィック表現から 2 つのベクトルを加算または減算する手順です。
平行四辺形法は、非常に簡単に使用できる手法であるため、ベクトルの加算と減算 (グラフィックス上) で最もよく使用されます。たとえば、物理学では、力を加えたり引いたりするために使用されます。
一方、ベクトルを加算するか減算するかによってルールが若干異なるため、以下では両方のバージョンを個別に説明します。
2 つのベクトルを加算するための平行四辺形の規則
2 つのベクトルをグラフィカルに追加する場合、平行四辺形の法則または法則を適用する手順は次のとおりです。
- まず、ベクトルを描画し、同じ適用点に配置します。つまり、両方のベクトルの原点を同じ点に配置します。
- 次に、一方のベクトルの端に、もう一方のベクトルに平行な線を描きます。そして、他のベクトルでも同じステップを繰り返します。したがって、平行四辺形の描画が得られます (これがルールの名前の由来です)。
- 最後に、合計の結果として得られるベクトルは、ベクトルの共通原点から 2 本の平行線の交点に向かう平行四辺形の対角線になります。
次の一般的な例では、平行四辺形の規則がどのように使用されているかを確認できます。

平行四辺形の規則を練習したい場合は、次のリンクで、より多くの例といくつかの解決済みベクトル加算の演習を参照できます。このページでは、ベクトルをグラフィカルに追加する他の方法や、数値的にベクトルを追加する方法も説明します。
2 つのベクトルを減算するための平行四辺形の規則
平行四辺形の規則または方法は、グラフから 2 つのベクトルを減算するためにも使用されます。したがって、ベクトル減算の手順は次のとおりです。
- まず、グラフ上で 2 つのベクトルを表し、それらを同じ適用点に配置します。つまり、両方のベクトルの原点を同じ点に配置します。
- 次に、演算で減算されるベクトルの逆のベクトルを描画します。つまり、減算されるベクトルを反転します。
- 次に、合計が になるベクトルの終わりに、符号変化ベクトルに平行な線を描きます。そして、他のベクトルでも同じプロセスを繰り返します。これにより、平行四辺形の描画が行われます (これがルールの名前の由来です)。
- 最後に、減算の結果は、2 つのベクトルの共通原点から 2 つの平行線が交差する点までのベクトルになります。
2 つのベクトルが平行四辺形の法則によって減算される次の一般的な例を見てください。
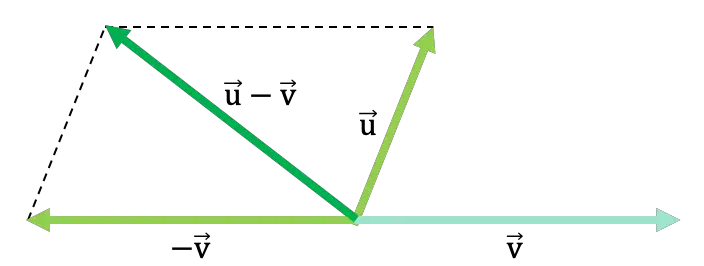
次のリンクでは、平行四辺形規則を使用したベクトル減算のその他の例を確認できます。また、解決されたベクトル減算の演習を使用して練習することもできます。さらに、グラフからベクトルを減算するための他のテクニックと、最終的には数値的にベクトルを減算する方法を説明します。
最後に、このテクニックの説明が役に立ったなら、右手の法則が何であるかについても知りたいと思うでしょう。リンク ページでは、それが何であるか、どのようなベクトル演算に使用されるか、および存在するこのルールのさまざまなバリエーションを確認できます。