ここでは変化率、平均変化率、瞬間変化率とは何かについて説明します。変化率の計算方法に関するいくつかの例を見ることができ、さらに、変化率に関する段階的な演習を解いて練習することができます。
変化率はどれくらいですか?
数学では、関数の変化率 (TV) は、2 つの異なる点における関数の値の差です。したがって、2 点間の変化率を計算するには、これら 2 点における関数の値を減算する必要があります。
![]()
たとえば、関数の 2 つのイメージが f(2)=1 および f(5)=7 である場合、それらの変化率は次のようになります。
![]()
変化率の数学的意味を見てきましたが、経済学における変化率の概念は次のことを意味します。
経済学では、2 つの値間の変化率は、パーセンテージで表されるそれらの差です。つまり、異なる期間間の変数の変化率は、その相対的な変化です。したがって、変化率を計算するには、2 つの異なる期間の値が減算され、得られた結果が最初の期間の値で除算されます。
![]()
たとえば、特定の株式の価値が 1 か月で 35 ユーロから 50 ユーロに増加した場合、その変化率は次のようになります。
![]()
変化率の 2 つの考えられる意味を考慮して、この記事では変化率の数学的定義を理解することに焦点を当てます。変化率には、平均変化率と瞬間変化率の 2 種類があります。以下にそれぞれのタイプについて説明します。
平均変化率
区間内の関数の平均変化率 (TVM) は、その独立変数が増加する単位ごとに関数が増加 (または減少) する単位数です。したがって、関数の平均変化率は、ある区間における関数の成長をその同じ区間の振幅で割ることによって計算されます。
![]()
平均変化率がどのように計算されるかを理解できるように、以下に例を段階的に解決しました。
関数の平均変化率の計算例
- 次の関数の区間 [2.5] における平均変化率を計算します。
![]()
まず、x=2 と x=5 での関数の値を計算します。
![]()
![]()
次に、次の式を適用するだけで、区間内の関数の平均変化率を計算します。
![]()
![]()
TVM[2,5] の結果が正であるため、関数が区間 [2,5] で増加することを意味します。一方、結果が負であった場合は、この区間で関数が減少することを意味します。
平均変化率の幾何学的解釈
幾何学的には、区間内の関数の平均変化率は、区間の極点を結ぶ線の傾きを表します。
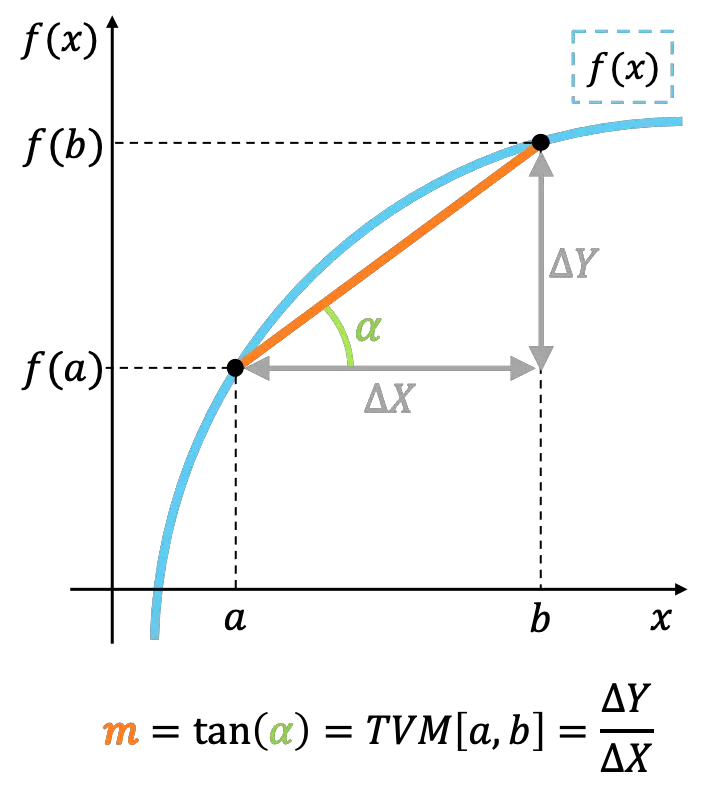
瞬間変化率
ある点における関数の瞬間変化率 (TVI) は、ある区間にわたる関数の相対的な増加の微小限界です。したがって、瞬間変化率は、 hがゼロに近づくことによってf(a+h)-f(a)の商の極限を解くことによって計算されます。
![]()
瞬間変化率の値は正、負、ゼロのいずれかであり、その時点での関数がそれぞれ増加、減少、またはその時点で同じままであることを意味します。
関数の瞬時変化率の計算例
- 次の関数の点 x=2 における瞬間的な変化率を計算します。
![]()
瞬間的な変化率を計算するには、次の式を適用する必要があります。
![]()
![]()
注目すべきアイデンティティを解決します。
![]()
➤注目すべき恒等式の公式をもう覚えていない場合は、多項式を専門とする当社のサイト ( www.polinomios.org ) ですべての公式を見つけることができます。
それでは、制限を解いてみましょう。
![]()
しかし、ゼロ間の不確定性がゼロであることがわかります。したがって、次のようになります。
![]()
➤参照: ゼロ間の不確定性がゼロの極限を解く方法
そして最後に、制限を解決します。
![]()
まだ:
![]()
TVI(2) の結果は正なので、関数が x=2 で増加することを意味します。一方、結果がマイナスだった場合は、この段階で機能が低下していることを意味します。
瞬間変化率の幾何学的解釈
幾何学的には、ある点における関数の瞬間的な変化率は、同じ点における関数に接する線の傾きを表します。
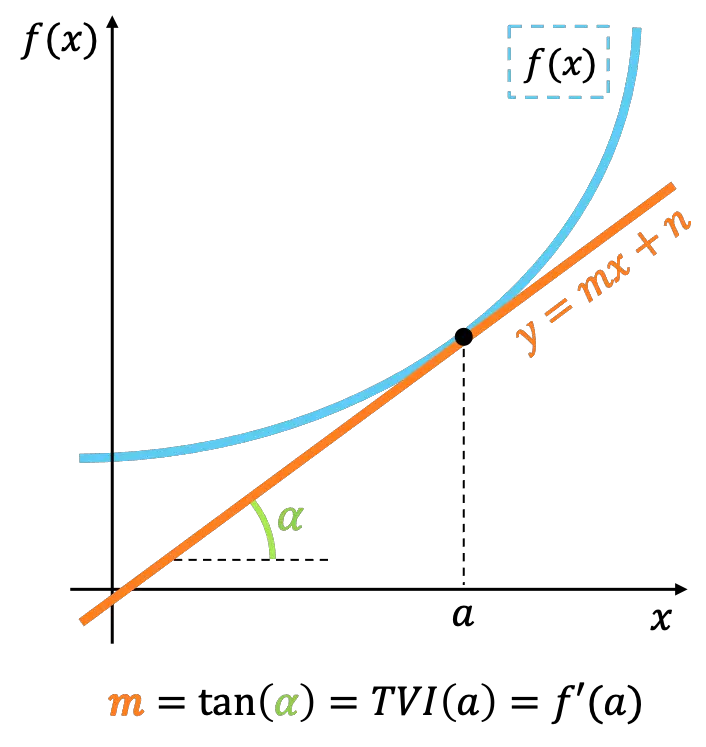
よく見ると、瞬間変化率の意味は関数の導関数の概念に相当します。したがって、瞬間変化率は、ある点における関数の導関数の値を計算するためにも使用されます。
変化率に関する演習を解決しました
演習 1
区間 [1,3] における次の関数の変化率の値を計算します。
![]()
まず、間隔の終わりの関数の値を決定します。
![]()
![]()
次に、変化率の公式を適用します。
![]()
![]()
演習 2
区間 [1,4] にわたる次の関数の平均変化率 (TVM) を計算します。
![]()
まず、x=1 と x=4 での関数のイメージを計算します。
![]()
![]()
そして、平均変化率の公式を適用します。
![]()
![]()
演習 3
区間 [-1.3] における次の関数の平均変化率を求めます。
![]()
平均変化率を決定するには、まず f(-1) と f(3) を計算する必要があります。
![]()
![]()
ここで、平均変化率の公式を使用します。
![]()
![]()
演習 4
次のグラフに示す関数の区間 [2,4] の平均変化率を計算します。

平均変化率の公式を適用します。
![]()
![]()
式でわかるように、f(4) と f(2) の値を見つける必要があります。これは、関数のグラフィカル表現を見ることで簡単に行うことができます。
![]()
![]()
関数の値がわかったので、それを式に代入します。
![]()
演習 5
点 x=2 における次の関数の瞬間変化率を計算します。
![]()
点 x=2 における関数の瞬間的な変化率を決定するには、対応する公式を適用します。
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73ee822823f921f75014cb9b50e47f51_l3.png)
演習 6
点 x=1 における次の関数の瞬間変化率 (TVI) を求めます。
![]()
瞬間的な変化率の公式を適用します。
![]()
![]()
次に、計算します
![]()
そして
![]()
![]()
![]()
そして、制限内で見つかった値を置き換えます。
![]()
私たちは注目すべき製品を解決します:
![]()
それでは、制限を解いてみましょう。
![]()
しかし、ゼロをゼロで割った不定形が見つかるので、分数の分子の多項式を因数分解して単純化します。
![]()
➤ゼロ間のゼロ不確定性を解く方法がわからない場合は、上のリンクで、ゼロ間のゼロ不確定性による極限を解く方法に関する完全な説明を参照してください。
そして最後に、制限を解決します。
![]()
要約すると、点 x=1 における関数の瞬間的な変化率は 2 に等しくなります。
![]()
演習 7
次の関数の点 x=2 における瞬間的な変化率を求めます。
![]()
まず、瞬間変化率の公式を使用します。
![]()
![]()
計算します
![]()
そして
![]()
![]()
![]()
そして、制限内で見つかった値を置き換えます。
![Rendered by QuickLaTeX.com \text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ad59f5f751af139656a471bf2a41801_l3.png)
注目すべき等式を計算します。
![]()
分子を操作します。
![]()
それでは、制限を解いてみましょう。
![]()
しかし、不確定性ゼロをゼロで割った値が得られるので、多項式を因数分解して単純化します。
![]()
そして最後に、制限を解決します。
![]()
まだ:
![]()