方程式系は、複数の未知数を持つ 2 つ以上の方程式のセットです。したがって、システムを解決するには、置換、等化、削減、グラフ化の 4 つの方法を使用できます。ただし、解決手順の説明を始める前に、解決の数に応じて存在するシステムのタイプを定義します。
- 決定された互換性のあるシステム:解は 1 つだけあり、単一点 (これが解) で交差する 2 本の線で表すことができます。
- 不確定互換システム:無限の解が存在します。これは、同じ点で一致する 2 本の直線があるためです。
- 互換性のないシステム:線が平行で共通点がないため、解決策がありません。
連立一次方程式を解く方法
ここで、連立方程式を解くために使用できるさまざまなシステムについて説明します。説明には理論といくつかの例が含まれており、説明されているすべての概念がより明確になります。この記事では、 2×2 方程式系についてのみ説明することに注意してください。これは、2 つの方程式で構成される系を単に扱うことを意味します。ということで、まずは説明から始めましょう。
置換法
代入法は、方程式の 1 つで未知数の 1 つを分離し、得られた式を反対の方程式に代入することで構成されます。この方法は、未知数の少なくとも 1 つの係数の値が 1 に等しい場合に最も推奨されます。したがって、従うべき手順は非常に簡単です。
- 2 つの方程式のうちの 1 つから未知の量を分離します。
- 最初の方程式から削除した未知数に相当する式を、もう一方の方程式に代入します。
- 得られた方程式の逆の未知数を消去します。
- 最初の変数の値を取得したら、それを使用して 2 番目の変数を見つける必要があります。
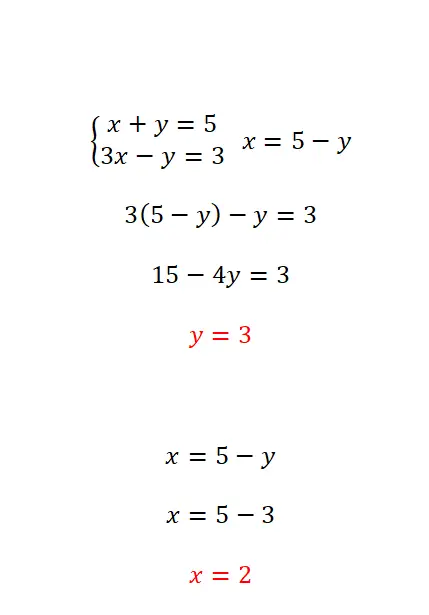
イコライゼーション方法
マッチング方法は、 2 つの方程式内の同じ変数を分離し、得られた 2 つの式をマッチングすることで構成されます。この方法は、計算全体が容易になるため、両方の方程式で同じ未知数を簡単に分離できる場合に推奨されます。この場合に従う必要がある手順は次のとおりです。
- 2 つの方程式で選択した未知数を分離します。
- この未知のものに等価な表現を同化します。
- この方程式を普通に解きます。
- 計算した値を使用して、もう一方の未知数を計算します。
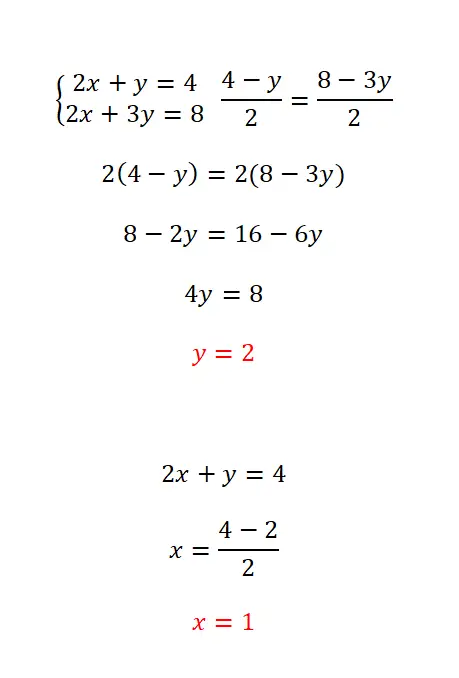
削減方法
この削減方法は、両方の式に 2 つの数値を乗算することに基づいており、これにより、両方の式の変数の 1 つの符号が異なる同じ係数を取得できます。この方法は、同じ未知数がすべての方程式で同じ係数を持つ場合、または反対符号の同じ係数を持つ場合に最も推奨されます。そして、解決手順は次のとおりです。
- 2 つの方程式に必要な数値が乗算されます (2 つの方程式の 2 つの変数の 1 つについて同じ係数を取得できるようにする 2 つの数値を見つける必要がありますが、符号は反対です)。
- 次に、方程式を減算または加算して、それぞれの係数を使用してこの未知数を除去します。
- 次に、残りの方程式を解きます。
- そして、この方程式の結果を使用して、他の変数で欠落している数値を取得します。
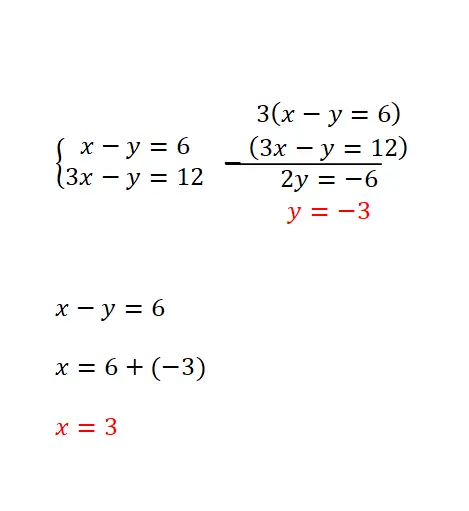
グラフィックメソッド
最後に、グラフ表現を使用して連立方程式を解くことを選択できます。この方法は他の方法とは大きく異なり、複雑な数学的部分はなく、ほぼ完全にグラフィカルです。したがって、未知数の値を知るには、2 つの方程式を直線の方程式y = mx + bの形式で構築する必要があります。このようにして表現を行うことができ、2 つの関数間のカットポイントの座標の値を未知数と関連付けます。以下に実際の例を示します。
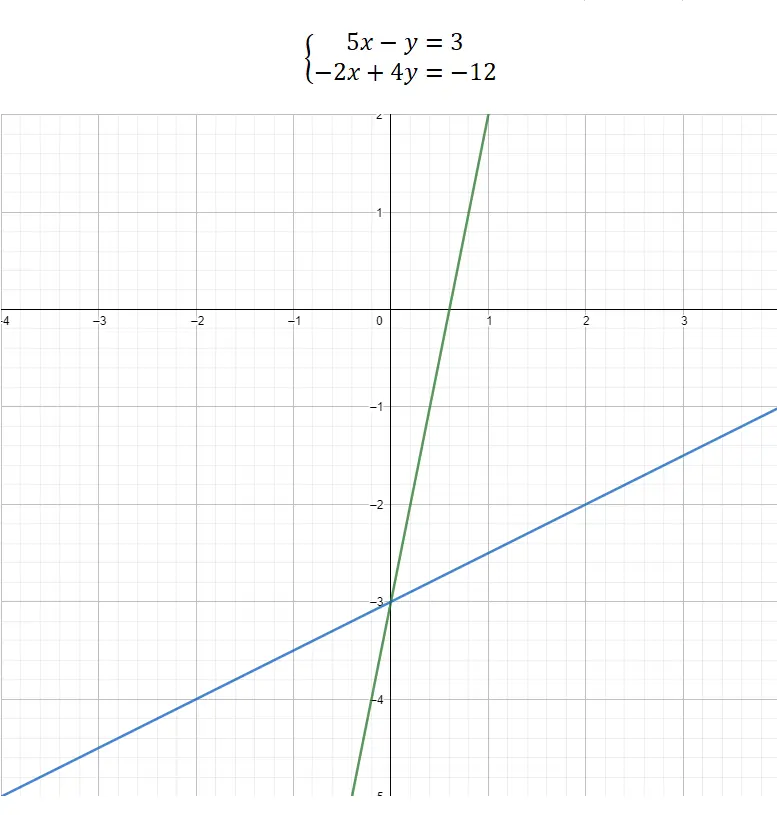
グラフからわかるように、2 つの関数間のカットオフ ポイントは (0, -3) です。したがって、x の値 = 0、y の値 = -3 となります。これは、連立方程式をグラフィカルに解く方法です。
連立二次方程式を解くにはどうすればよいでしょうか?
二次方程式系を解くには、今説明した方法を使用できます。個人的には、単一の未知数の方程式を迅速に取得できる置換法をお勧めします。一方、リダクションやイコライゼーションの手法を使用すると、計算が非常に複雑になります。したがって、2 つの変数のいずれかを代入したら、結果として得られる2 次方程式または2 次方程式を解くだけで済みます。プロセス全体を確認できる例を次に示します。
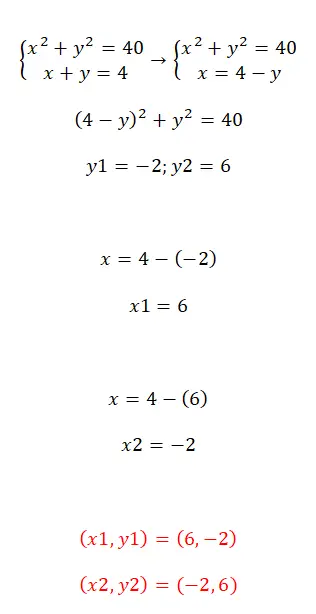
連立方程式を解く演習
ここで、説明した理論を適用できるように、一次方程式および二次方程式系に関するいくつかの演習を提供します。こうすることで、連立方程式の計算に関連するすべての概念をよりよく理解できるようになります。私たちが提供する答えを見る前に、問題を解いてみることをお勧めします。こうすることで演習を最大限に活用できます。
演習 1
置換法を使用してこの連立方程式を解きます。
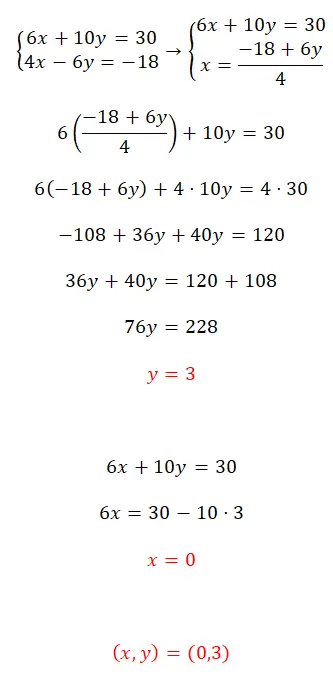
- まず、方程式内の 2 つの未知数のうち 1 つを分離します。
- 次に、逆の方程式で得られた式を、以前に解いた未知数に置き換えます。
- 次に、反対の変数の結果を取得します。
- 次に、最初に発見された値を 2 つの方程式のいずれかに代入して、最初の未知の値を計算します。
- 最後に、2 つの変数の結果を表します。
演習 2
置換法を使用してこの連立方程式を解きます。
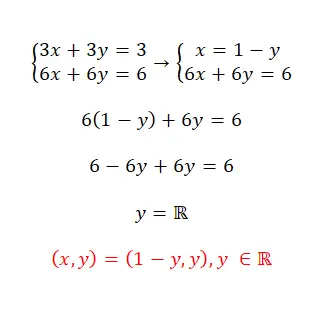
- この場合も同じ手順に従います。未知のものを分離し、それを他の式に置き換えて、2 番目の変数を分離します。
- ご覧のとおり、これは無限に多くの解があるため、互換性が不確定なシステムです。
演習 3
等化法を使用してこの連立方程式を解きます。
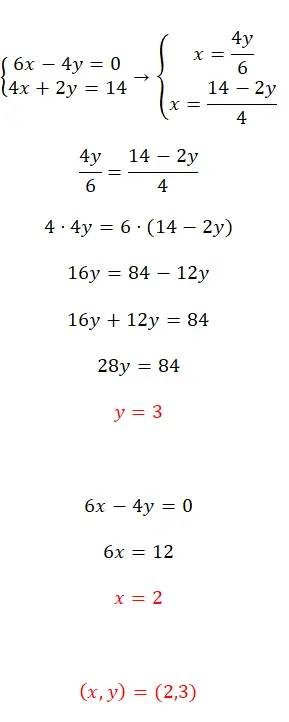
- 最初のステップは、両方の方程式の同じ変数を分離することです。この場合は x を選択しました。
- 次に、結果の式を照合して、解決を開始します。
- したがって、最初の未知の値が得られます。
- そして、それを 2 つの元の方程式の 1 つに代入すると、2 番目の未知数を計算できます。
- 最後に、2 つの変数の結果を表します。
演習 4
等化法を使用してこの連立方程式を解きます。
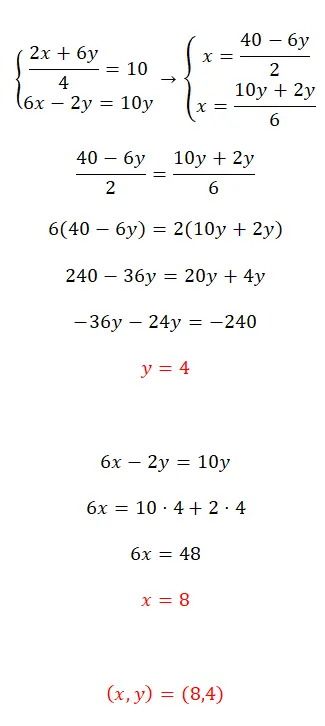
- まず、両方の方程式の x を分離します。
- 次に、取得した式を照合します。
- 最初の未知数の値を取得します。
- この値を 2 つの初期方程式の 1 つに代入し、2 番目の未知数を計算します。
- 最後に、見知らぬ二人の価値を表現します。
演習 5
リダクション法を使用してこの連立方程式を解きます。
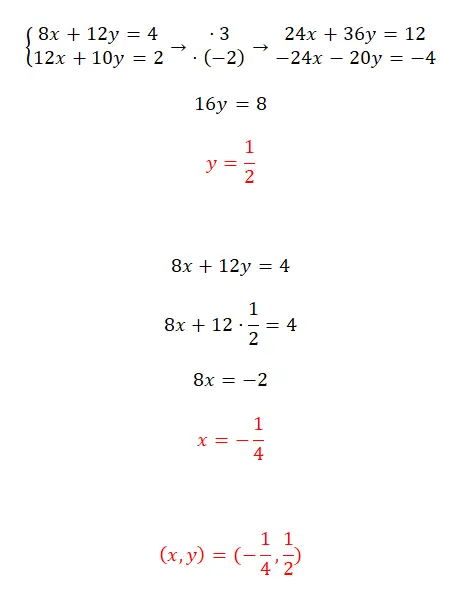
- 2つの方程式の 2 つの変数の 1 つに対して同じ係数を取得できるようにする、符号が反対の 2 つの数値を探す必要があります。
- 次に、得られた 2 つの式を加算して得られる方程式を単純に解きます。
- 次に、y を 2 つの元の方程式のいずれかに代入して、x を計算します。
- 最後に、システムの結果を表現します。
演習 6
リダクション法を使用してこの連立方程式を解きます。
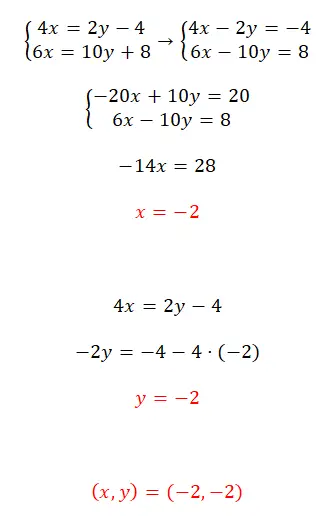
- まず、方程式を整理します (すべての変数を左に渡します)。
- 次に、最初の式に -5 を掛けます。
- 2 つの方程式を加算して得られる方程式を解き、x の値を取得します。
- この既知の値を使用して y の値を取得します。
- 連立方程式の結果を表現します。
演習 7
置換法を使用してこの連立方程式を解きます。
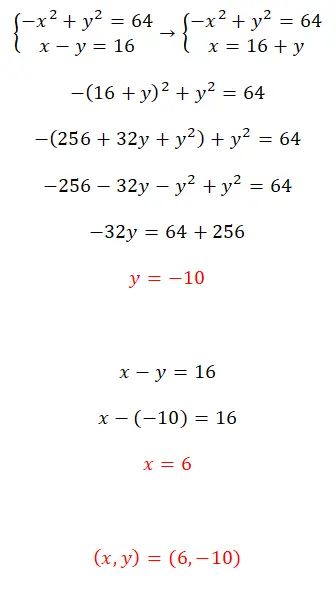
- この非線形方程式系を解くには、置換法を使用することをお勧めします。
- したがって、x に相当する式を使用して方程式を作成します。
- 未知の y の値を取得します。
- 以前に計算した値を使用して x の値を計算します。
- そして、あなたはすでに両方の値を持っています。
演習 8
選択した方法を使用して、この連立方程式を解きます。
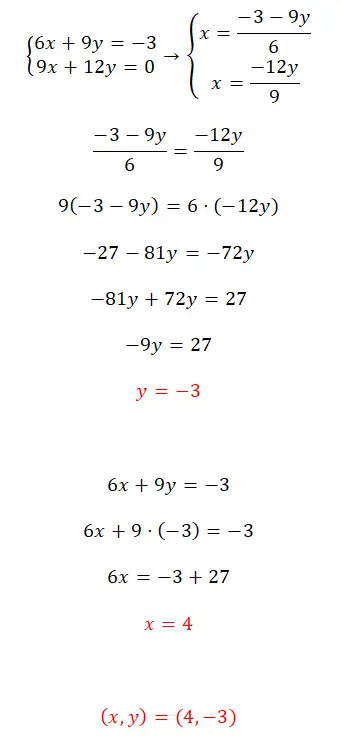
- この場合、決定された互換性のあるシステムが提示され、等化手法を使用してそれを解決します。
- したがって、両方の方程式の x を解き、結果として得られる 2 つの式を等しく設定します。
- 方程式を解くと、y の値が得られます。
- この値を使用して x の値を見つけます。
- 最後に、システムの結果を表現します。