この記事では、定数関数とは何か、またそのグラフ表現とは何かについて説明します。さらに、定数関数のいくつかの例と、このタイプの関数のすべての特性を確認できます。そして最後に、定数関数の解いた演習でトレーニングできるようになります。
定数関数とは何ですか?
定数関数は、独立変数 (x) の任意の値に対して常に同じイメージを取る関数です。つまり、定数関数はf(x)=kという形式になります。ここで、k は任意の実数です。
![]()
定数関数のグラフィック表現は水平線です。
たとえば、次の関数はすべて定数です。
![]()
定数関数のグラフ表示
定数関数の概念を理解したら、グラフで定数関数を表現する方法がわかります。
定数関数のグラフ作成は非常に簡単で、関数の値 (k) に水平線を引くだけです。
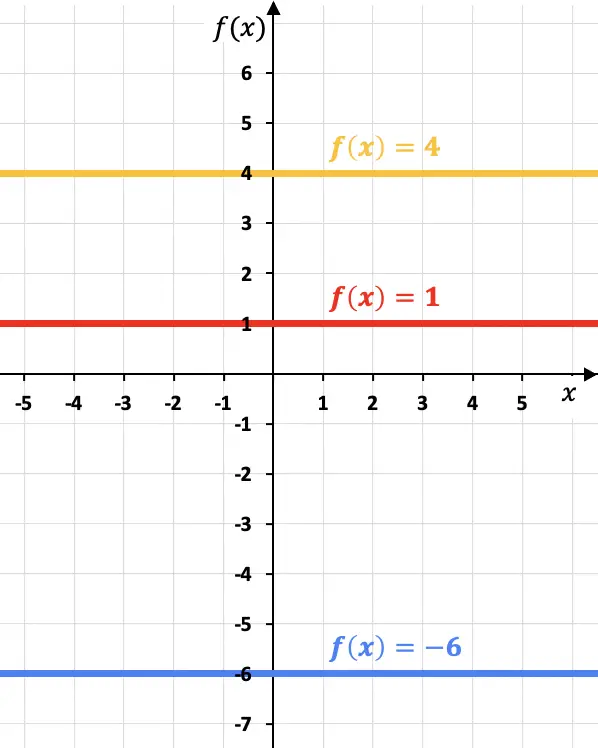
グラフ上で 3 つの異なる定数関数を表現した次の例を見てください。

各定数関数は x 軸に平行であることに注意してください。
一方、垂直線は定数関数ではないことに留意する必要があります。実際、垂直線は関数ですらない。定義上、関数は x の値ごとに 1 つの画像しか持てないからである。
定数関数の特徴
次に、定数関数のプロパティを分析します。任意の値の定数関数を考えてみましょう。
![]()
- 定数関数の定義域はすべて実数です。
![]()
- 定数関数のパスまたは範囲は定数の値のみです。
![]()
- 関数は常に同じ値を取るため、これは連続的で偶数な関数です。
![]()
- 定数関数は増加も減少もせず、常に傾きが 0 になる関数の一種です。
![]()
- これは常に点 (0,k) で OY 軸と交差します。
![]()
- すべての定数関数は 0 次の多項式です。
- うん
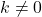
定数関数にはルートがありません。代わりに、
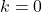
すべての実数は定数関数の根です。
- x がプラス無限大またはマイナス無限大に近づくときの定数関数の限界は、定数の値と等しくなります。
![]()
![]()
- 定数関数の導関数は常にゼロです。
![]()
実際、定数関数の定義は導関数の概念からも行うことができます。つまり、関数の導関数が領域全体で消える場合、関数は定数となります。
- 定数関数の積分は線形 (またはアフィン) 関数です。
![]()
➤ 「 一次関数とは何ですか?」を参照してください。
区間上の定数関数
関数がどのように定数であるかを見てきましたが、関数はその領域の区間内でのみ定数になることができます。
この概念を理解するには、どの関数がチャンクで定義されているかを知る必要があるため、先に進む前に次の説明を参照することをお勧めします。
➤ 「区分関数とは何ですか?」を参照してください。
これらのタイプの関数が何であるかを理解したら、以下に示す部分で定義されている関数を見てください。

グラフからわかるように、関数はその定義域内のすべての数値にわたって一定ではありません。ただし、区間 [-2,4) では定数であるため、1 つの区間でのみ定数関数となります。
定数関数の修正された問題
演習 1
次の関数のうちどれが定数であるかを特定します。
![]()
最初の機能は、
![]()
は、変数 x の値が何であっても常に 4 であるため、定数関数です。
2番目の機能は、
![]()
、関数の値は x の値に応じて変化するため、定数関数ではありません。アフィン関数です。
3つ目の機能は、
![]()
は、x のどの値に対しても常に 0 に等しいため、実際には定数関数です。
4つ目の機能は、
![]()
, は x の値に応じて変化するため、定数関数ではありません。これは一次関数です。
演習 2
点 (0.6) を通過する定数関数を求めます。
代数的には、定数関数の式は常に同じ形式になります。
![]()
そして、グラフィカルに定数関数は常に水平線であるため、定数関数の座標は常に等しく、値が異なります。
![]()
関数が通過する点の座標は y=6 であるため、この問題で探している定数関数は次のようになります。
![]()
演習 3
次の定数関数を同じグラフにプロットします。
![]()
各定数関数を表すには、各定数の高さに水平な直線を引くだけです。