このページでは、多項式の除算、単項式による多項式の除算と、別の多項式による多項式の除算の両方の方法を説明します。また、多項式の除算の例を確認し、段階的に解決された演習で練習することもできます。さらに、この多項式演算のプロパティもわかります。
多項式 (または多項式) の除算
2 つの多項式がどのように除算されるかを正確に見る前に、使用する方法を理解しやすくするために、多項式の除算の概念を簡単に確認します。
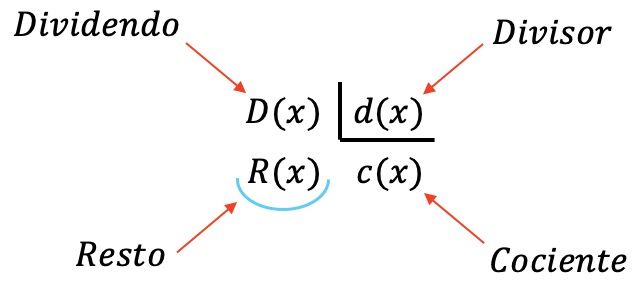
多項式の除算には 4 つの多項式が関係します。
- 配当: 分割多項式。
- Divisor : 被除数を除算する多項式。
- 商: 被除数を除数で割った結果。
- 剰余(または剰余): 2 つの多項式を除算したときに残る多項式。
一方で、多項式間には 2 種類の割り算があることも知っておく必要があります。
- 多項式の正確な除算: 剰余がゼロの場合、多項式間の除算は正確です。この場合、多項式の被除数は、除数に商を乗算した値に等しくなります。
![]()
また、この場合の配当金は、
![]()
は約数の倍数です
![]()
そして商
![]()
同様に、多項式の約数と多項式の商はどちらも被除数の約数です。
- 多項式の整数除算: 多項式の整数 (または不正確) 除算では、剰余は非ゼロ (0) になります。この場合、多項式除算の基本特性が満たされます。
![]()
多項式の除算とは何かを理解したので、多項式を互いに除算する方法を見てみましょう。より正確には、最初に多項式と単項式の間の除算を説明し、次に 2 つの多項式の間の除算を説明します。
多項式を単項式で除算する
多項式を単項式で割る方法を説明する前に、まず単項式がどのように分割されるかを思い出してください。このタイプの多項式演算を実行するには、それを知っておく必要があるからです。
2 つの単項式の除算には、それらの係数を相互に除算し、リテラル部分を相互に除算することが含まれます。つまり、単項式の係数が除算され、同じ底を持つ変数の指数が減算されます。次の例を見てください。
![]()
ここで、単項式による多項式の除算がどのようなものになるかを見てみましょう。
数学では、多項式を単項式で除算する場合、多項式の各項を単項式で除算します。
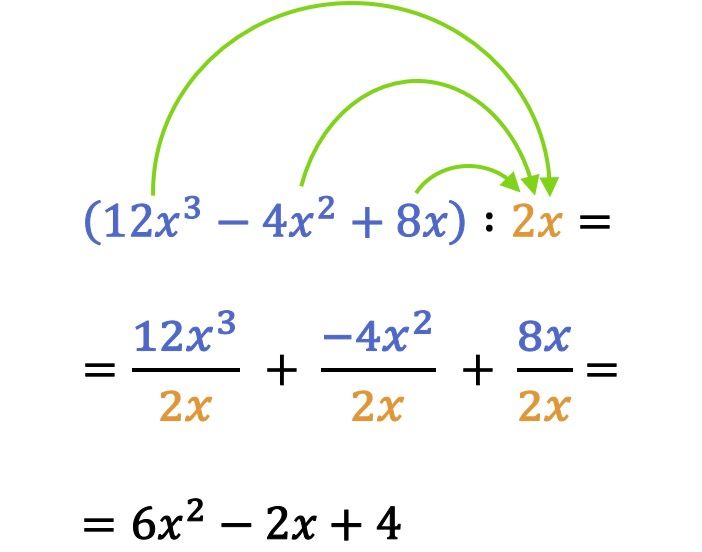
前の除算の例では、単項式または多項式を除算するときに、符号の規則も考慮する必要があることに注意してください。実際、多項式と単項式の割り算でよくある間違いは、項の符号を間違えることです。
多項式を別の多項式で除算する
2 つの多項式を除算するには、手順に従う必要があります。そのため、例を段階的に解いて、多項式の除算 (多項式の長期除算とも呼ばれます) の方法がどのようなものかを見てみましょう。
- 多項式の除算結果を計算します。

多項式の間
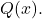
2 つの多項式であること:
![]()
![]()
最初に行うことは、多項式を除算形式に変換することです。左側に分数の分子 (被除数多項式) を書き、右側に分数の分母 (除数多項式) を置きます。
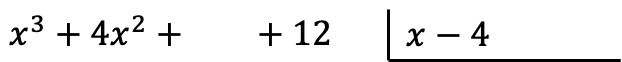
警告:多項式に特定の次数の単項式がない場合は、その場所にスペースを残す必要があります。たとえば、多項式
![]()
1 年生の学期はありませんので、その代わりに空白のスペースが生じます。
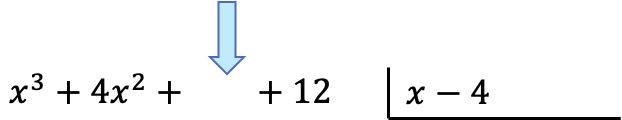
多項式を用意したら、商を求めます。そして、商の第 1 項を求めるには、被除数の第 1 項を除数の第 1 項で割る必要があります。
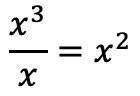
そして、商の代わりに除算の結果を代入します。
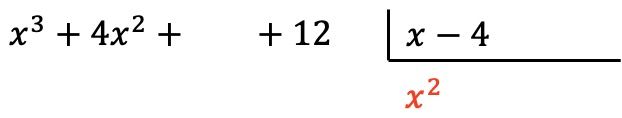
次に、除数の各要素で見つかった項を乗算し、各結果を対応する列の被除数の下に置き、その符号を変更します。
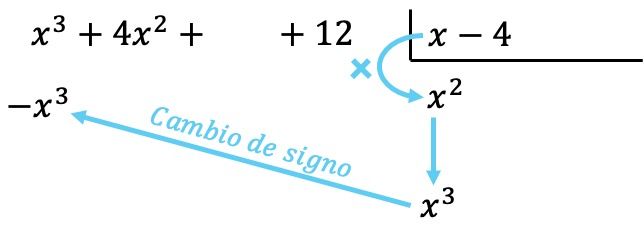
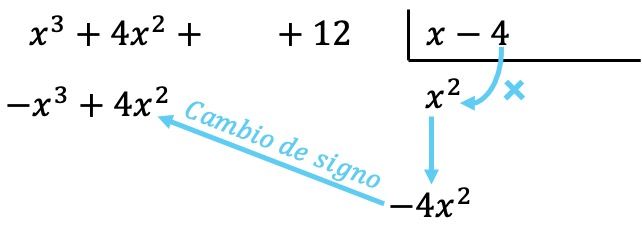
多項式を使用するすべての演算と同様、同じ次数のすべての項が同じ列に収まるように、多項式を最高次数から最低次数の順に並べることが重要です。
乗算結果を反対の符号で配置したら、垂直方向に整列した項を追加する必要があります。
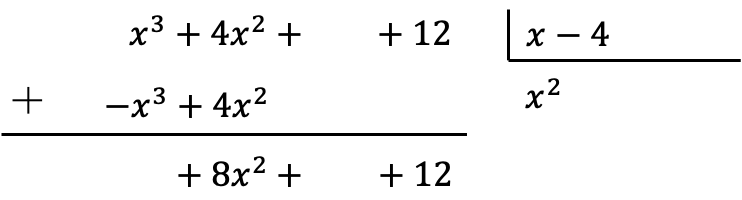
この合計を行うと、最高次数の係数が相殺されるため、被除数の項が 1 つ少なくなることに注意してください。
次に、多項式の被除数が多項式の除数より 1 次小さくなるまで、同じ手順を繰り返す必要があります。
したがって、配当の最初の項を除数の最初の項で割ります。
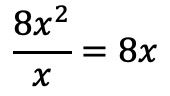
結果を商に代入します。
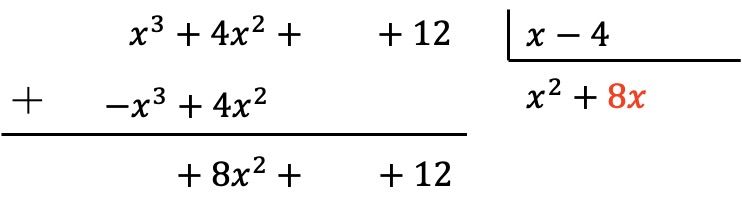
前と同様に、商の新しい項に除数の各要素を乗算し、逆符号の結果を被除数の対応する列に入れます。
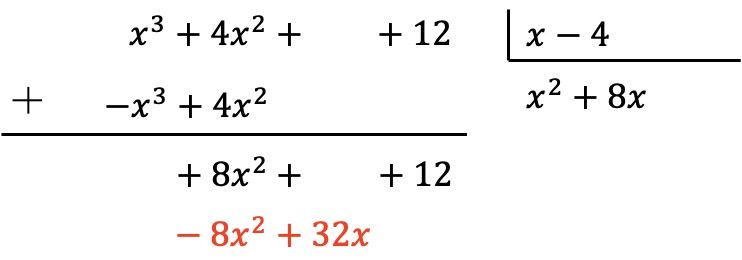
そして垂直方向に次のように追加します。
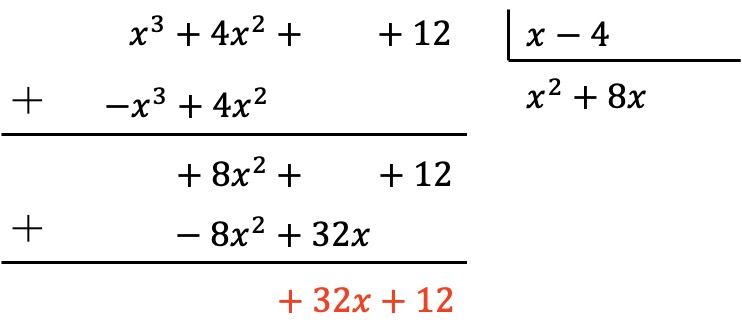
被除数多項式は依然として除数多項式より 1 次も小さいため、同じプロセスを継続する必要があります。
したがって、最初に被除数の最初の項を除数の最初の項で除算し、次にその結果に除数の各項を乗算し、次に変更した結果を被除数に符号を付けて、最後に垂直方向に加算します。
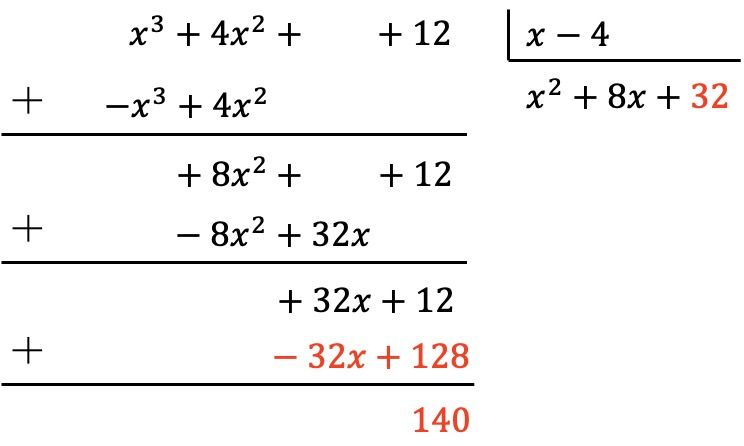
したがって、被除数の次数が 0 で除数が 1 次であるため、被除数の多項式の次数が除数の次数より小さいことがすでに得られています。したがって、除算は完了です。
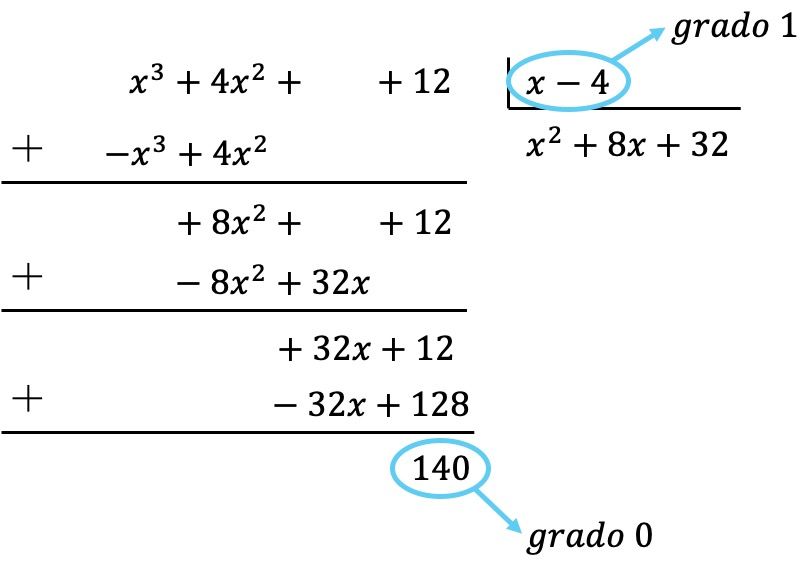
したがって、除算の結果は次のようになります。
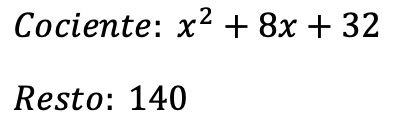
一方、多項式の除算の基本条件に基づいて、多項式の除算が正しく実行されたことを検証できます。
![]()
![]()
![]()
![]()
✅
方程式が満たされているため、多項式の除算が正しく実行されました。
これで多項式の除算は終わりました。この説明がお役に立てば幸いです。多項式の分割方法についてどう思いましたか?疑問はありますか?あなたはそれが好きですか?それとも、多項式の除算が存在しない方が良いでしょうか? 😂 コメントを読んでいます! 👇👇👇
除算多項式の性質
多項式のどの除算も次の特性を満たします。
✓多項式の被除数の次数は、常に多項式の除数の次数より大きくなければなりません。
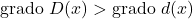 ✓多項式の被除数の次数は、除数と商の次数の合計に相当します。
✓多項式の被除数の次数は、除数と商の次数の合計に相当します。
![]()
✓剰余の次数は常に、除数の次数 (したがって、被除数の次数も) よりも小さくなります。
![]()
✓配当は、除数と商と剰余を掛けた積に等しくなります。この条件は数の割り算にも当てはまります。
![]()
多項式の除算に関する演習を解決しました
演習 1
次の多項式を単項式で除算した結果を求めます。
![]()
多項式を単項式で割るには、多項式の各項の単項式による除算を解く必要があります。
![Rendered by QuickLaTeX.com \begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffa558b26adc36e2ac45a842a6cf33df_l3.png)
単項式間で除算する場合、係数はそれらの間で除算され、底が同じであるべき乗の指数が減算されることに注意してください。
演習 2
次の多項式の単項式による除算を計算します。
![]()
多項式を単項式で割るには、多項式の各項をその単項式で割る必要があります。
![Rendered by QuickLaTeX.com \begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868da1546d3e4d33e8226774020cbb2d_l3.png)
単項除算では、係数が係数同士で除算され、底が等しい累乗の指数が減算されることに注意してください。
演習 3
次の多項式の単項式による除算を解きます。
![]()
多項式を単項式で割るには、多項式の各項の単項式による除算を解く必要があります。
![Rendered by QuickLaTeX.com \begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8d5fe46b397f2f531a865e7cb0df3cf_l3.png)
除算単項式は負であるため、すべての除算の符号が変化することに注意してください。
演習 4
次の多項式の除算を実行します。
![]()
多項式を除算するには、上で説明した方法を適用する必要があります。
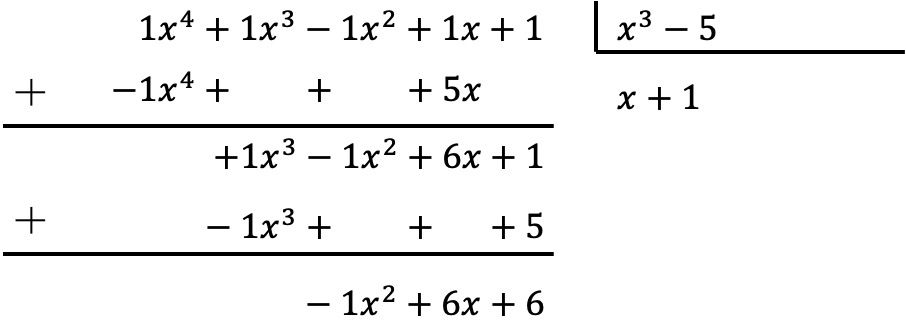
したがって、2 つの多項式間の除算の結果は次のようになります。
商:
![]()
休む:
![]()
演習 5
次の多項式の除算を計算します。
![]()
二項式による多項式の除算を解決するには、上で見た方法を適用する必要があります。
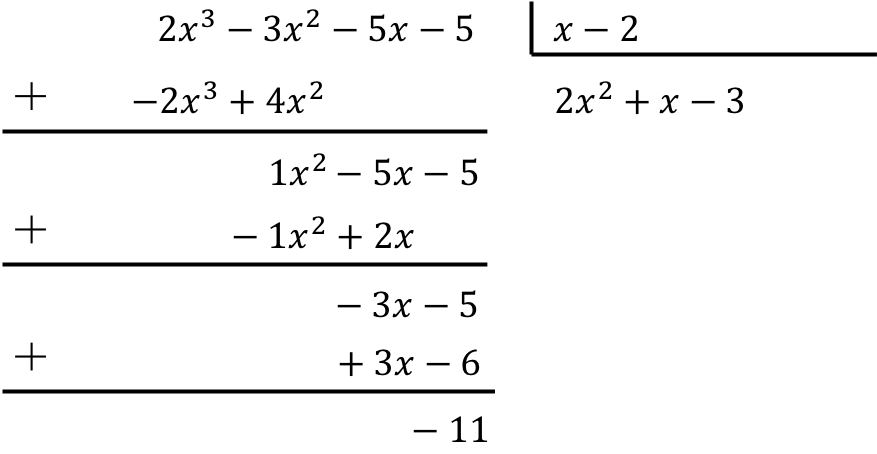
したがって、多項式除算の結果は次のようになります。
商:
![]()
休む:
![]()
演習 6
次の多項式の割り算を解きます。
![]()
多項式の除算を計算するには、説明した方法を適用する必要があります。
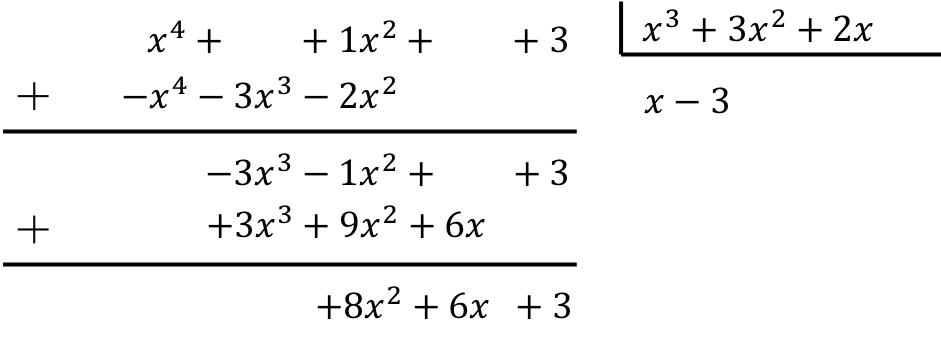
したがって、2 つの多項式間の除算の結果は次のようになります。
商:
![]()
休む:
![]()
演習 7
2 つの多項式間の次の除算の結果を求めます。
![]()
多項式を三項式で除算するには、説明した方法を適用する必要があります。
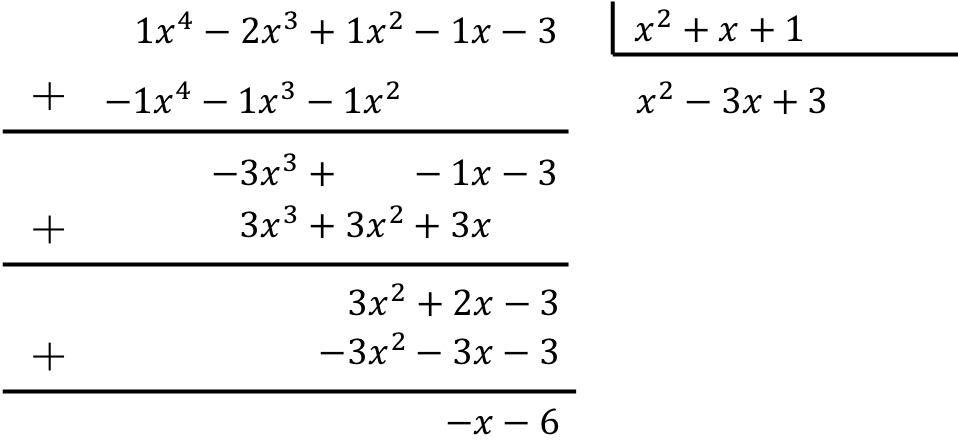
したがって、2 つの多項式間の除算の結果は次のようになります。
商:
![]()
休む:
![]()
👉👉👉ここまで理解できたということは、多項式がどのように分割されるかをすでに知っていることを意味します。明るい!多項式の割り算をマスターしたので、多項式間の特定の割り算をより迅速に解くことができる方法があることを知ってください。これは合成除算またはルフィニ ルールです。リンクをクリックすると、このトリックがどのように適用されるか、いつ使用できるかを確認できます。😉