多項式の数値

このページでは、多項式とは何か、および多項式の数値を計算する方法を説明します。さらに、多項式の数値を段階的に解く例題や演習も見ることができます。

多項式の数値は何ですか?

数学では、値 x=a に対する多項式 P(x) の数値、つまり P(a) は、多項式の変数 x を数値 a に置き換え、次の計算を実行することによって得られる結果です。多項式で。

多項式の数値の概念をよりよく理解できるように、例を使用して多項式の数値がどのように計算されるかを以下に示します。

多項式の数値を計算する方法

多項式の数値の数学的定義がわかったので、例を使用して多項式の数値を決定する方法を見てみましょう。

  • 次の多項式の x=2 の数値は何ですか?

P(x)=x^3+5x^2-4x+1

多項式の数値を求めるには、問題で与えられた値でその多項式を評価する必要があります。つまり、変数を代入する必要があります。

x

ステートメントの値による多項式の計算。したがって、この場合、文字を置き換える必要があります

x

2の場合：

P(2)=2^3+5\cdot 2^2-4\cdot 2+1

そして、その値を多項式の代数式に代入したら、演算を実行します。したがって、最初にべき乗を解きます。

P(2)=8+5\cdot 4-4\cdot 2+1

次に、乗算を計算します。

P(2)=8+20-8+1

最後に、項を加算および減算します。

\bm{P(2)=21}

結論として、x=2 の多項式の数値は 21 に等しくなります。

ご覧のとおり、多項式の数値を求めることはそれほど複雑ではありませんが、非常に便利な応用がいくつかあります。たとえば、多項式に関する非常に重要な定理である剰余定理を使用できるようにするには、多項式の数値を求める方法を知ることが不可欠です。このリンクをクリックして剰余定理とは何かを調べてください。その説明、使用例、および演習が段階的に解決されています。

多項式の数値例

多項式の数値を取得する方法を理解できるように、他の解決例を示します。

例1

  • 多項式の数値を計算します

    P(x)=x^3-2x^2+3x+6

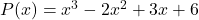
    のために

    x=-1.

\begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}

この場合、多項式の数値は 0 に等しくなります。 因数定理のおかげで、多項式間の特定の除算の余りが何になるかを知ることができるため、これには多項式の特性による影響があります。詳細については、前のリンクをクリックしてください。そこでは、この定理の内容とその目的が説明されています。

例 2

  • 多項式の数値を決定する

    P(x)=-2x^3+7x^2-8x-2

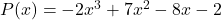
    のために

    x=3.

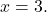
\begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}

ここまでは、古典的な方法で多項式の数値を決定する方法のみを見てきましたが、別の方法があることを知っておく必要があります。具体的には、ルフィニ法を使用して多項式の数値を計算することもできます。この手順の使用方法も知っておく必要があるため、リンク内の詳細な説明を確認することをお勧めします。

2 つ以上の変数を含む多項式の数値

変数が 1 つしかない多項式の数値を見つける方法を説明しました。しかし…多項式に複数の変数がある場合、どのようにして多項式の数値を取得するのでしょうか?

多項式に 2 文字以上の文字がある場合、その数値は同じ方法で計算する必要があります。つまり、まず多項式の各変数を対応する値に置き換えてから、多項式演算を解きます。

例として、このタイプの問題は以下のように解決されます。

  • 多変量多項式の数値を求める

    P(x,y)=x^2y+4xy-2x^2+6y-5

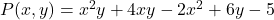
    価値観のために

    x=2, y=3.

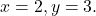
まず、各変数を対応する値に置き換えます。つまり、文字を置き換えます。

x

2の場合は文字を変更します

y

3までに：

P(2,3)=2^2\cdot 3+4\cdot 2\cdot 3-2\cdot 2^2+6\cdot 3-5

力を求めて解きます。

P(2,3)=4\cdot 3+4\cdot 2\cdot 3-2\cdot 4+6\cdot 3-5

ここで積を計算します。

P(2,3)=12+24-8+18-5

そして最後に、加算と減算を行います。

\bm{P(2,3)=41}

したがって、命令データの多項式の数値は 41 に相当します。

多項式の数値に関する演習を解決しました。

演習 1

x=-2 の場合の多項式 P(x) の数値はいくらですか?

P(x)=-2x^3-4x^2+3x+8

多項式の数値を見つけるには、ステートメントで指定された値を多項式に代入し、結果の演算を解くだけです。

\begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}

演習 2

x=4 の場合、分数を使用して次の多項式の数値を計算します。

P(x)=\cfrac{1}{2} x^2-\cfrac{5}{4}x + 7

多項式に分数があるかどうかに関係なく、多項式の数値を求める手順は常に同じです。したがって、変数 x を 4 に置き換えて計算を解く必要があります。

\begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}

演習 3

x=3、y=5、z=-2の値に対する多項式の数値を決定します。

P(x,y,z)=x^2yz+4y^2z^2-3x^2z+6xyz

多変量多項式の数値を決定するには、問題で指定された値を代数式に代入し、結果の演算を解くだけで十分です。

\begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}

演習 4

多項式を考えると

P(x)= -2x^3-3x^2+5x+k

パラメータ値を計算する

k

となることによって

P(-2)=5.

この問題では、未知の値を求めるには、

k

方程式を解く必要があります

P(-2)=5.

P(-2)=5

したがって、最初に P(-2) の値を計算してみます。

\begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}

ここで、得られた式を 5 に等しくします。

P(-2)=5

-6+k=5

そして最後に、結果として得られる方程式を解きます。

k=5+6

\bm{k=11}

コメントする

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

上部へスクロール