ここでは、多項式のすべての部分 (次数、変数、独立項など) が何であるか、およびそれらがどのように呼ばれるかについて説明します。さらに、いくつかの例を確認し、解決された演習で多項式の一部を練習することができます。
ただし、多項式のすべての部分が何であるかを確認する前に、概念を完全に理解するためにその数学的定義を簡単に確認しましょう。多項式は、さまざまな次数の単項式の加算または減算によって形成される代数式です。
多項式の各部分は何ですか?
多項式の部分は次のとおりです。
- 項: 多項式の各単項式部分。
- 係数: 多項式の各項に付随する数値。
- 次数: 多項式変数を累乗する最大の指数。
- 変数: は多項式が持つ文字です。
- 主項: 多項式の最高次項です。
- 独立項: 変数を含まない多項式の項。
- 支配係数: 多項式の支配項の係数。
多項式に変数が 1 つだけある場合、その次数はその項の最大の指数に等しくなります。ただし、多項式に 2 つ以上の変数がある場合は、演算を実行する必要があるため、次数を知ることがさらに困難になります。 2 つ (またはそれ以上) の変数の多項式の次数については、次のリンクをクリックして、これがどのように行われるかを調べてください。
多項式の部分を識別する方法
多項式の部分または要素は視覚的に簡単に見つけることができます。次の図でこれがどのように行われるかを見てください。
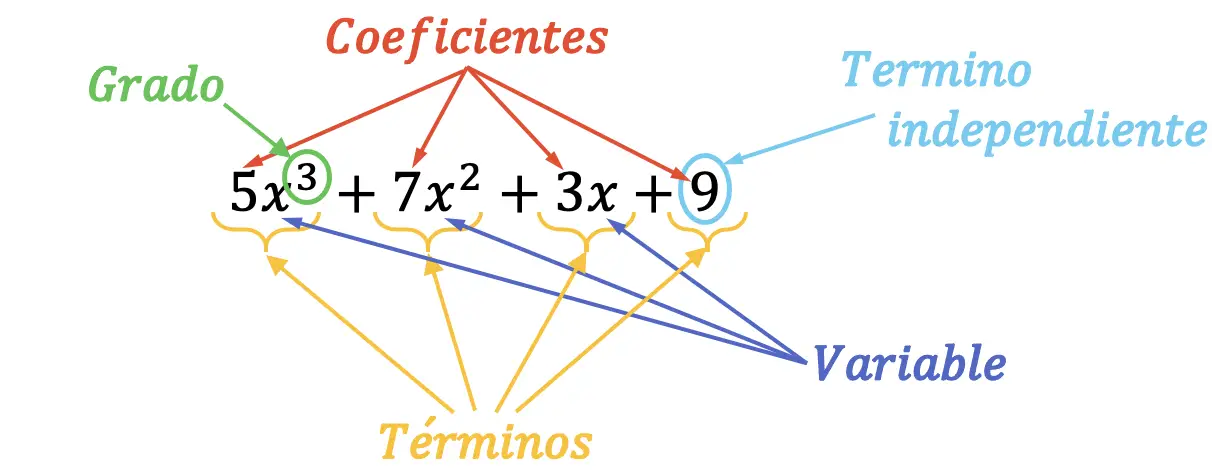
前の多項式は 3 次であり、そのすべての部分がマークされています。さらに、前記多項式の主項は、最高次数の 単項式であるため、約 5x 3です。同様に、多項式の先頭係数は先頭項の係数であるため、5 になります。
この場合、多項式の変数は 1 つであるため、次数のタイプは 1 つだけです。ただし、多項式が多変数の場合は、変数の絶対次数と相対次数を区別する必要があることを知っておく必要があります。それぞれが何で構成されているかは、上に置いたリンクで確認できます ⬆⬆ ( 2 変数の多項式の次数)。
多項式の各部分の例
多項式の各部分の意味とそれらが実行する関数を理解するために、あらゆるタイプの多項式の部分を決定する例をいくつか見ていきます。
例1
次の 2 次 (2 次) 多項式の各部分を特定します。
![]()
- 項: 4x 2 、-8x、1
- 係数: 4、-8、1
- 2年目
- 変数: x
- メインターム:4× 2
- 独立した権限: 1
- ステアリング係数:4
一方、この例の多項式は3 項式と呼ばれることに注意してください。このタイプの多項式が何であるかは、三項式の例で確認できます。さらに、二項と呼ばれる別のタイプの多項式にも興味があるかもしれません (これを使用するといくつかの演算を行うのが簡単です)。二項の例でその特別な点を確認できます。
例 2
次の多項式の部分を見つけます。
![]()
- 用語: y 3 、9y 2 、-5y、3
- 係数: 1、9、-5、3
- 3年目
- 変数: および
- メインターム: および3
- 独立した権限: 3
- ステアリング係数:1
この例でわかるように、単項式の前に数値がない場合、その係数は 1 であることを意味します。したがって、この多項式の主要係数は 1 に等しくなります。
多項式の部分の演習問題を解決しました。
多項式のすべての部分の名前を覚えやすくするために、解決済みの演習をいくつか用意しました。それらに関する質問はすべてコメント欄で受け付けています。 ⬇⬇
演習 1
次の多項式のすべての部分を求めます。
![]()
すべての項は少なくとも 1 つの変数 (または文字) で形成されるため、この演習の多項式には独立した項がありません。
用語: 2×4、6×2 、 x
係数: 2、6、1
レベル4
変数: x
メインターム: 2×4
独立した用語: しない
ステアリング係数:2
演習 2
次の多項式のすべての部分を求めます。
![]()
この問題の多項式は、x と y の 2 つの変数で構成されます。まだ:
項: -7x 4 y 2 、3x 4 、-5y 2 、xy、-10
係数: -7、3、-5、1、-10
6年目
変数: x、y
メインターム: -7x 4および2
独立した権限: -10
ステアリング係数:-7
ご覧のとおり、このような多項式を解くには、複数の変数を含む多項式の次数を計算する方法を知る必要があります。これを行う方法がまだわからない場合は、上の「多項式の部分とは何ですか?」のリンクを確認することをお勧めします。 ( 2 つの変数の多項式の次数)。 ⬆⬆ ステップバイステップの説明といくつかの例が表示されます。
これは根本的に異なる概念ですが、ここまで来たら、数値の多項式が何であるかを知ることにきっと興味を持つでしょう。これはあまり知られていないことですが、実際には非常に便利です。