このページでは因数定理とは何かについて説明します。さらに、因子定理が多項式の割り算、根の求め、多項式の因数分解などに使用されることを示します。最後に、因子定理に関するステップバイステップの演習を行うことができます。
因数定理とは何ですか?
数学では、因数定理は、P(a)=0 の場合に限り、多項式 P(x) が形式 (xa) の別の多項式で割り切れることを示します。
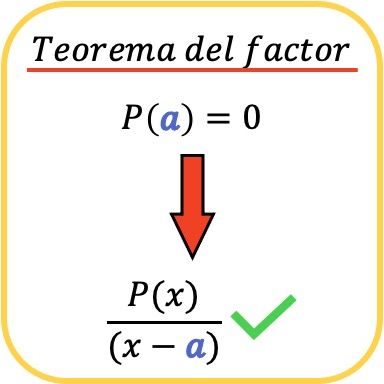
同様に、因子定理の結果として、多項式 P(x) が項 (x−a) で割り切れる場合、値 a が多項式 P( x の根 (またはゼロ) であることを意味します。 )。
1 つの多項式が別の多項式で割り切れるということは、2 つの多項式間の割り算の余り (または余り) がゼロに等しいことを意味します。この概念を完全に覚えていない場合は、次のリンクで多項式の除算の例を見ることができます。そこには、多項式の除算方法の説明と段階的に解決される演習もあります。
因子定理の例
因子定理の数学的定義を理解したところで、それがどのように適用されるかをいくつかの例を見てみましょう。
例1
因数定理の応用の 1 つは、指定された多項式が二項式で割り切れるかどうかを調べることです。これを因子定理でどのように行うか例を見てみましょう。
- 多項式 P(x) が二項 Q(x) で割り切れるかどうかを判断します。両方とも次のとおりです。
![]()
まず、除数多項式 Q(x) は (xa) 型の多項式であるため、因子定理を適用して問題を解決できます。
したがって、P(x) を Q(x) で除算できるかどうかを確認するには、x=1 の場合の多項式 P(x) の数値を計算する必要があります。1 は符号が変更された除算多項式の独立項であるためです。 :
![Rendered by QuickLaTeX.com \begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00216efc4a2e53b0b38de1175e73a5bd_l3.png)
x = 1 における多項式 P(x) の数値はゼロになるため、因数定理によれば、P(x) は Q(x) で割り切れます。つまり、両方で割った余りは null になります。
2 つの多項式をルフィニの定理で除算することで、割り算条件が満たされていることを確認できます。
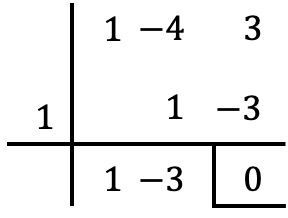
この例からわかるように、因子定理は剰余 (または剰余) 定理の特殊なケースです。 剰余定理とは何かを説明するこの記事を残しておきます。また、剰余定理を使って解決される例や演習も紹介します。さらに、剰余定理と因数定理の違いもわかるようになります。
例 2
因数定理は、多項式の根 (またはゼロ) を見つけるために使用することもできます。しかし、明らかに、この種の問題を理解するには、 多項式の根が何であるかを知る必要があります。この概念がまだ理解できない場合は、リンク先のページで詳しく説明されていますのでご覧ください。
それでは、多項式の根を見つけるために因子定理がどのように適用されるかを例を通して見てみましょう。
- 多項式 P(x) が与えられた場合、その根の 1 つが x=2 であるかどうかを計算します。
![]()
因数定理を適用すると、項 x=2 は、x=2 の P(x) の数値が 0 の場合にのみ多項式 P(x) の根になります。したがって、次の数値を見つける必要があります。
![Rendered by QuickLaTeX.com \begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-82d50f0361613cb6c540051f8da4bc20_l3.png)
実際、多項式 P(x) の数値は x=2 で消滅するため、因数定理のおかげで、x=2 が多項式 P(x) の根であると断言できます。
因数定理を使用した多項式の因数分解
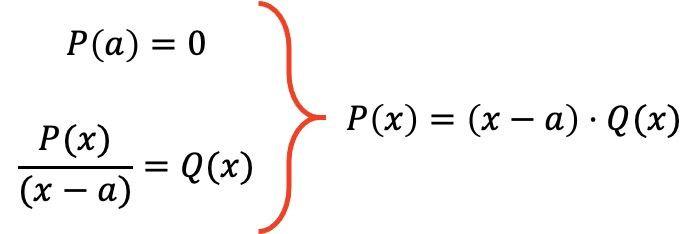
因数定理のもう 1 つの応用は、多項式の因数分解です。それが何であるかわからない場合のために説明すると、多項式の因数分解とは、多項式の式を因数の積に変換することを意味します。つまり、多項式を因数分解すると、その代数式が簡素化されます。
したがって、階乗定理は、多項式 P(x) が与えられた値 a に対して P(a)=0 を満たす場合、その多項式の式を積 P(x)=(xa)・Q( x)、ここで Q(x) は、多項式 P(x) を (xa) で除算した結果得られる多項式です。
例として、階乗定理を使用して次の多項式を因数分解します。
![]()
前の多項式から、x=-2 の多項式の数値がゼロに等しいため、x=-2 がその根の 1 つであることがわかります。
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d94a4657a385e672badeabd7458b376_l3.png)
したがって、ルッフィーニの規則を使用して、x によって形成される二項式とこの符号が変更された根、つまり因数 (x+2) の間の多項式 P(x) を分割します。
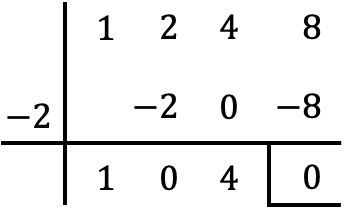
したがって、多項式の除算の商は次のようになります。
![]()
そして最後に、因子定理から、因子 (x+2) と前の除算で得られた商の乗算の形で多項式 P(x) を表すことができます。
![]()
したがって、多項式 P(x) を部分的に因数分解しました。多項式を完全に因数分解するには、より長い手順を適用する必要があります。私たちは、ルフィニ多項式を因数分解する方法を段階的に説明するガイドを作成しました。さらに、この記事では、すべての種類の因数分解を説明し、解決された演習で練習することができます。したがって、リンクをクリックして、セットから多項式を因数分解する方法を確認してください。
因数定理の問題を解いた
次に、因数定理を段階的に解く練習問題をいくつか用意しました。これにより、この定理を理解しているかどうかを確認することができます。自分で試してみて、解決策を正しく理解しているかどうかを確認することをお勧めします。また、下記のコメント欄に質問を残していただくこともお忘れなく! ❓❓💬💬
演習 1
階乗定理を使用して、多項式 P(x) が二項 Q(x) で割り切れるかどうかを調べ、割り切れる場合は、多項式の根を見つけて因数分解します。
![]()
この場合、多項式の約数 Q(x) は、x と独立項のみから構成される二項式になります。したがって、階乗定理を使用して多項式 P(x) を他の多項式 Q(x) で除算できることを示すには、符号を変えた除数多項式の独立項で多項式 P(x) の数値を評価する必要があります。つまり、x=3 の場合:
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e8ac752f8e16fae1d66386e9d2a02a0_l3.png)
x=3 における多項式 P(x) の数値は 14 に相当します。つまり、ゼロとは異なります。したがって、因数定理によれば、割り算の余りはゼロではないため、P(x) は Q(x) で割り切れません。
演習 2
階乗定理によって、多項式 P(x) が二項 Q(x) で割り切れるかどうかを調べ、割り切れる場合は、多項式 P(x) の根を見つけて因数分解します。
![]()
この場合、多項式の約数 Q(x) は x と独立項のみで構成される二項式であるため、階乗定理を適用できます。
そして、多項式 P(x) が多項式 Q(x) で除算できるかどうかを確認するには、多項式 Q(x) の符号を変えた独立項に対する多項式 P(x) の数値を見つける必要があります。つまり、x=-1 の場合:
![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34b63772a1b44bee2c746d94b6ca4785_l3.png)
この問題では、x=-1 における多項式の数値はゼロであるため、P(x) は Q(x) で割り切れます。
次に、階乗定理によって、x=-1 における P(x) の数値が消えるため、x=-1 が多項式 P(x) の根であると推定できます。
したがって、x=-1 は多項式 P(x) の根であるため、これを因数分解するには、単純に x+1 で除算します。このために、Ruffini メソッドを使用します。
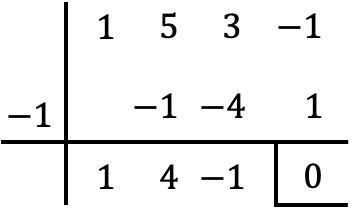
したがって、操作の結果は次のようになります。
![]()
したがって、次のように多項式 P(x) を因数分解できます。
![]()
演習 3
階乗定理を使用して、多項式 P(x) が二項 Q(x) で割り切れるかどうかを調べ、割り切れる場合は、多項式 P(x) の根も求めて因数分解します。
![]()
この場合、Q(x) を割る多項式は x と独立項のみで構成される二項式となるため、因数定理を利用できます。
そして、多項式 P(x) が多項式 Q(x) で割り切れるかどうかを確認するには、多項式 Q(x) の符号を変えた独立項に対する多項式 P(x) の数値を決定する必要があります。つまり、x =-3 の場合:
![Rendered by QuickLaTeX.com \begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef8bb895fe041193d71351ffadb94f2f_l3.png)
この場合、x=-3 における多項式の数値はゼロであるため、確かに P(x) は Q(x) で割り切れます。
このため、P(-3) はゼロに等しいため、階乗定理から x=-3 が多項式 P(x) の根であると推定します。
したがって、x=-3 は多項式 P(x) の根であるため、それを因数分解するには、それを x+3 で除算する必要があります。このために、ルフィニの法則を使用します。
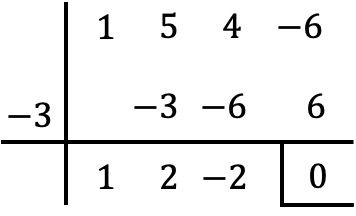
したがって、除算の結果は次のようになります。
![]()
したがって、次の方法で多項式 P(x) を因数分解できます。
![]()
因数定理についてどう思いますか?それは代数に役立つと思いますか?コメントを読んでいます!
👀⬇⬇⬇👀