このページでは、和の二乗の公式、つまり注目すべき恒等式 (a+b) 2を見つけることができます。また、二乗和の例題や解答済みの演習も見ることができます。そしてさらに、この注目すべき製品に隠された幾何学的特性を発見するでしょう。
和の二乗とは何ですか?
和の 2 乗は注目すべき恒等 (または注目すべき積) の 1 つであり、2 つの正の項を 2 乗した二項の累乗をすばやく計算できる数学的規則です。
したがって、和の二乗は、2 つの異なる項を加算して二乗したもので構成されます。つまり、和の二乗の代数式は(a+b) 2です。
和の二乗の公式
この注目に値するタイプのアイデンティティの数学的定義を踏まえて、和の 2 乗の公式が何であるかを見てみましょう。

したがって、和の 2 乗は、最初の項の 2 乗に、最初の項と 2 番目の項の積の 2 倍を加え、2 番目の項の 2 乗を加えたものに等しくなります。
したがって、二乗和を解くには、それぞれの加算を 2 にするだけでは十分ではなく、さらに、2 つの加算を一緒に 2 で乗算する必要があります。
これは覚えておくことが重要です。2 乗を加算するときによくある間違いは、2 つの項の間の積を忘れて 2 乗だけを計算してしまうことだからです。

式から用語を省略しないように注意してください。
一方、減算の 2 乗 (または減算の 2 乗) の公式は、今見たものとよく似ていますが、結果を完全に変える違いがあることに注意してください。それがどのようなものであるかわからない場合は、 二乗減算式とは何か、およびそれがどのように適用されるかをここで確認できます。
二乗和の例
ここでは、和を二乗する方法を理解できるように、いくつかの実際的な例を示します。
例1
- 式を適用して、次の二乗和を計算します。
![]()
二乗和の公式は次のとおりです。
![]()
まずパラメータを特定する必要があります
![]()
そして
![]()
式の。この場合、
![]()
を表します
![]()
ペアと
![]()
番号 5 に対応します。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
さて、私たちは今の価値を知っているので、
![]()
そしての
![]()
この式を適用して、合計の二乗の結果を求めることができます。

例 2
- 和の二乗について次の式を解きます。
![]()
和の二乗の公式は次のとおりです。
![]()
したがって、この問題では
![]()
単項式です
![]()
そしてその一方で、
![]()
は独立項 4 です。
![Rendered by QuickLaTeX.com \begin{array}{c} a=3x \\[2ex] b=4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-89bb3514fbd79ba368588655e152e9cc_l3.png)
最後に、の値を特定したら、
![]()
そしての
![]()
、注目すべき積を解くために二乗和の公式を適用します。
![Rendered by QuickLaTeX.com \begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ed0d9fcdbeeac2247b68789dd0268f37_l3.png)
和の二乗の公式の証明
次に、和の 2 乗から今見た公式を導き出し、それがどこから来たのかを理解します。
2 に累乗した正の二項から開始します。
![]()
上記のべき乗は明らかに因数と等価です
![]()
それ自体を乗算します:
![]()
したがって、分配プロパティを使用して 2 つの括弧を乗算します。
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
最後に、結果の用語から類似した用語をグループ化します。
![]()
そして、すでにこの式の多項式に到達しているため、次のように証明されています。
![]()
信じられないかもしれませんが、和の公式の 2 乗は2 次多項式の因数分解にも機能します。それが何であるかわからない場合のために説明すると、多項式因数分解は、多項式の式を単純化するために数学でよく使用される手順です。上のリンクをクリックして、その方法をご覧ください。
和の二乗の幾何学的解釈
これまで、和の二乗が数学的にどのように計算されるかを見てきましたが、この注目すべき積は幾何学的に解釈することもできます。
次の正方形の一辺を見てください。
![]()
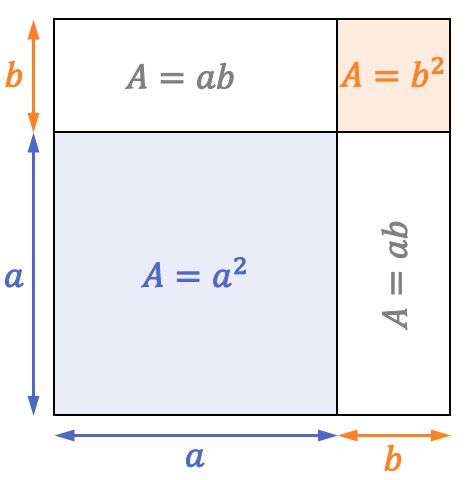
正方形の面積は、その一辺の長さを二乗した値に等しい。したがって、前の正方形の辺は次のようになります。
![]()
その面積(または表面積)は以下に等しい
![]()
さて、正方形の表現でわかるように、面積が の正方形です。
![]()
2つの領域を持つ長方形
![]()
そして別の正方形の表面
![]()
したがって、平方和の公式は幾何学的観点からも満たされます。
![]()
和の二乗の問題を解決しました
次に、演習を行って概念の理解を完了できるように、二乗和の演習をいくつか段階的に解いていきます。ご質問はすべてコメント欄にご記入ください。喜んでお答えいたします。 💭💭💭
演習 1
次の二乗和を求めます。
![]()
![]()
![]()
![]()
問題の注目すべき正体をすべて解決するには、和の二乗の公式を適用するだけで十分です。
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d696f9e8ea8a9246922a0aa132d7e24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
演習 2
次の式を適用して、2 つの項の二乗和を解きます。
![]()
![]()
![]()
問題の注目すべき積をすべて計算するには、二乗和の公式を使用する必要があります。
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8eaa03c68adc376819c5e12081f6d39_l3.png)
セクション B) では、根が二乗されると簡略化されることを覚えておく必要があります。
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a38b1df7ca331cb002253d52eb008608_l3.png)
最後の二乗和の単項式には分数係数があるため、これを解くには分数の性質も使用する必要があります。
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
演習 3
電卓を使用せずに、和の二乗の公式を適用して、次のべき乗を求めます。
![]()
まず、17 という数字は、10 プラス 7 の合計に分解できます。
![]()
そこで、電力を二乗和に変換しました。したがって、対応する式を適用できるようになりました。
![Rendered by QuickLaTeX.com \begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e35048f0ae6ae12bc2b5b3d761fb99_l3.png)
つまり、強化の結果は次のようになります。
![]()
この演習で説明したように、二乗和の公式は、電卓を使用せずに大きな数のべき乗を計算する場合にも役立ちます。
3項の和の2乗
場合によっては、追加された 3 つの項の 2 乗、つまり (a+b+c) 2を解く必要があることがわかるかもしれません。論理的には、このような場合には、括弧内に二項ではなく三項があるため、説明した公式は使用できません。したがって、別の式を使用する必要があります。
3 項の和の 2 乗の公式は次のとおりです。
![]()
この式がどのように適用されるかを例で見てみましょう。
![Rendered by QuickLaTeX.com \begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0816bbe156553fc1ef5920ac2b2e09f_l3.png)
ご覧のとおり、数式に 1 つの要素を追加すると、結果はさらに複雑になります。