このページでは、反エルミート行列 (アンチエルミート行列とも呼ばれる) が何であるかを説明します。反エルミート行列、そのすべてのプロパティ、およびこのタイプの複雑な正方行列の形状の例が見つかります。最後に、複素行列を反エルミート行列と別のエルミート行列の和に分解する方法について説明します。
反エルミート行列または反エルミート行列とは何ですか?
好奇心から、このタイプの行列はエルミート行列の逆の条件を満たすためそう呼ばれています。その名前は、19 世紀の数学の教授兼研究者であり、重要な研究を行ったフランスの重要な数学者シャルル エルミットに由来しています。線形代数の分野。
反エルミート行列の例
反エルミート行列 (または反エルミート行列) の定義を理解したら、さまざまな次元の反エルミート行列の例をいくつか見ていきます。
次数 2×2 の反エルミート行列の例
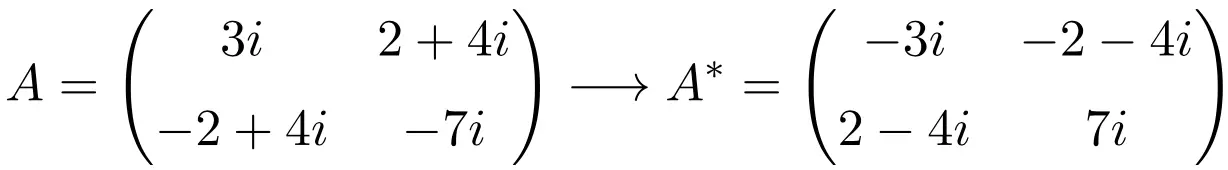
3×3 次元の反エルミート行列の例
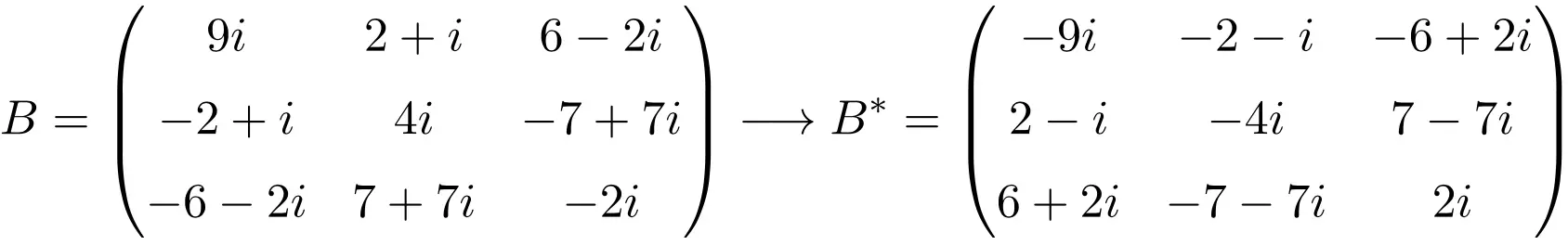
サイズ 4×4 の反エルミート行列の例
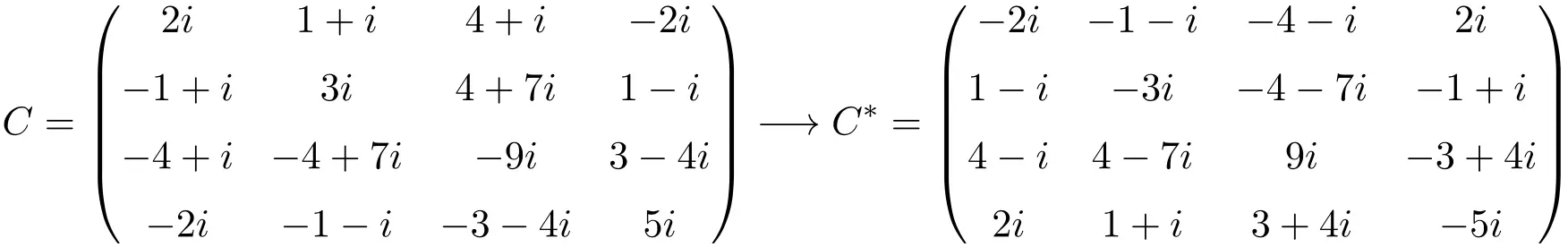
ご覧のとおり、行列 A、B、および C は、それぞれの共役転置行列が行列自体と等しいが、すべての要素の符号が変更されているため、反エルミート行列です。
反エルミート行列の構造
前の例をすでに見た場合、反エルミート行列は常に同じ構造を持っています。反エルミート行列は、主対角線上の虚数 (実数部なし) と、i 番目の行と j 番目の行にある複素数要素で構成されます。ライン。列は同じ虚数部と同じ実数部を持つ必要がありますが、j 行目および i 列目の要素として符号が変更されています。
これは少し複雑に見えるかもしれませんが、次の例で理解するとわかりやすいでしょう。
2×2 次元の反エルミート行列の構造
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f160fc8949e4256fcf771e7be11c517_l3.png)
ご覧のとおり、反エルミート行列の主対角要素は完全に虚数であり、副対角要素は同じ虚数部を持ち、実数部の符号が変更されています。
したがって、反エルミート行列の実部は反対称、虚部は対称でなければなりません。
反エルミート行列の性質
ここで、このタイプの正方複素行列のプロパティが何であるかを見てみましょう。
- 各反エルミート行列は正規行列の一例です。ただし、すべての通常の行列が反エルミティック行列であるわけではありません。
- あらゆる反エルミート行列は対角化可能です。さらに、結果として得られる対角行列には、純粋に架空の要素のみが含まれます。
- したがって、反エルミート行列の固有値 (または固有値) は常に虚数になります。
- 同様に、反エルミート行列の異なる固有値の固有ベクトル (または固有ベクトル) は直交します。
- 実数の行列、つまり虚数部を持たない要素は、それが非対称行列である場合に限り、反エルミート行列になります。
- 反エルミート行列は、実数の非対称行列と虚数の対称行列の和として表すことができます。
![]()
- 2 つの反エルミート行列の合計 (または減算) は、別の反エルミート行列と等しくなります。
- スカラーが実数の場合、反エルミート行列とスカラーの積の結果は、別の反エルミート行列になります。
- 指数が奇数の場合、反エルミート行列の累乗は反エルミート行列と等しくなります。一方、偶数乗の場合、結果はエルミート行列になります。
- うん

は反エルミート行列の場合、積は
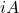
はエルミート行列です。
複素行列の反エルミート行列とエルミート行列への分解
複素数を含む行列は、反エルミート行列と別のエルミート行列の和に分解できます。ただし、そのためには、これらのタイプの行列の次の特性を理解しておく必要があります。
- 正方複素行列とその転置共役の合計は、エルミート (またはエルミート) 行列と等価です。
![]()
- 正方複素行列とその転置共役の差は、反エルミート行列に等しくなります。
![]()
- したがって、すべての複素行列はエルミート行列と反エルミート行列の和に分解できます。この定理はテオププリッツ分解として知られています。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-74e1d9a0d55d77dd927109e42986c200_l3.png)
ここで、C は分解したい複素行列、C* はその転置共役、そして最後に A と B はそれぞれ行列 C が分解されるエルミート行列と反エルミート行列です。