ここでは、関数の双曲線逆正接を導出する方法を説明します。また、このタイプの三角関数導関数の解決例も確認でき、最後に双曲線逆正接の導関数の公式を示します。
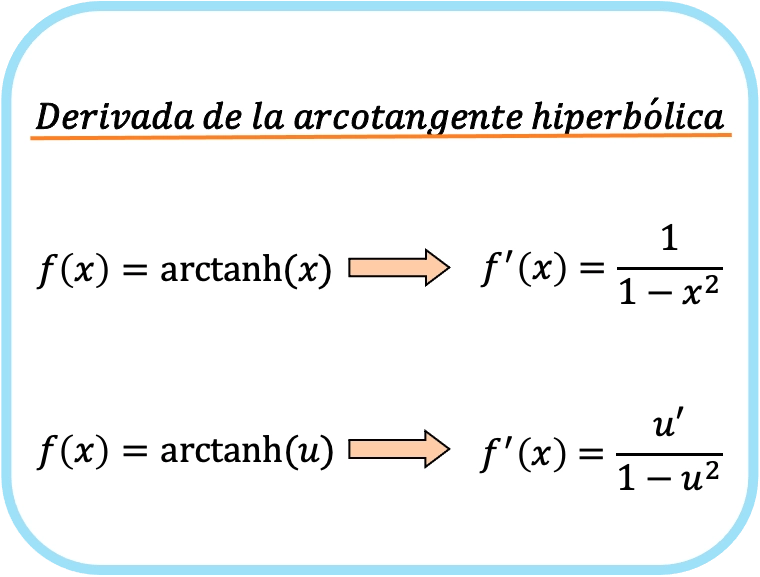
双曲線逆正接の導関数の公式
x の双曲線逆正接の導関数は、1 の 1 から x の 2 乗を引いたものです。
![]()
したがって、関数の双曲線逆正接の微分値は、その関数の微分値を 1 で割った商から、その関数の 2 乗を引いたものに等しくなります。
![]()
実際、両方の式は同じですが、2 番目の式では連鎖規則が適用されます。たとえば、x を u に置き換えると、x の導関数が 1 であるため、正確に最初の式が得られます。
逆正接が正接の逆関数であるのと同様に、双曲線逆正接は双曲線正接の逆関数です。それでも、それらの導関数は大きく異なります。この三角関数の導関数はここで確認できます。
➤参照: 双曲線正接の導関数の公式
双曲線逆正接の導関数の例
例1
![]()
論理的には、双曲線逆正接の導関数の法則を適用する必要があります。
![]()
2x の導関数は 2 なので、分数の分子に 2 を入れ、分母に 1 から 2x の 2 乗を引いたものを入れます。
![]()
例 2
![]()
この関数の導関数を解くには、双曲線逆正接の導関数の公式を使用する必要があります。
![]()
さらに、双曲線逆正接引数関数は複合関数であるため、連鎖規則も適用する必要があります。
![]()
双曲線逆正接の導関数の証明
この最後のセクションでは、双曲線逆正接の導関数の公式を示します。
![]()
双曲線逆正接は逆双曲線正接であるため、前の等式は別の方法で表現できます。
![]()
次に、方程式の両辺を微分します。
![]()
私たちはあなたをクリアします:
![]()
一方、双曲線余弦と双曲線正弦の二乗の差は 1 になることがわかっています。したがって、前の式を分数に変換できます。
![]()
![]()
分数のすべての項を双曲線余弦の二乗で割ります。
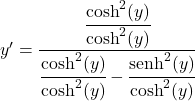
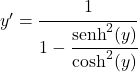
したがって、双曲線余弦間の双曲線正弦の商は双曲線正接に等しいので、次のようになります。
![]()
![]()
しかし、証明の最初で見たように、双曲線正接は変数 x と同等であるため、式を置き換えることができ、双曲線逆正接の導関数の式が得られます。
![]()
類似商品
- 双曲線余接の導関数の公式
- 逆余接微分公式
- 逆正接の微分公式
- コタンジェントの導関数式
- 接線の導関数の公式