双曲線正接の導関数

7月 3, 2023

ここでは、関数の双曲線正接の導関数が何であるかを確認します。さらに、双曲線正接の導関数の解決例をいくつか見ることができます。最後に、双曲線正接の導関数の公式を示します。

双曲線正接の導関数の公式

x の双曲線正接の導関数は、1 を x の双曲線余弦の 2 乗で割ったものに等しくなります。 x の正接の導関数は、x の双曲線正割の 2 乗、および 1 から x の双曲線正接の 2 乗を引いたものと等価です。

$\begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}$

一方、関数の引数に x 以外の関数がある場合は、連鎖規則を適用する必要があります。そして、双曲線正接の導関数の 3 つの公式は次のとおりです。

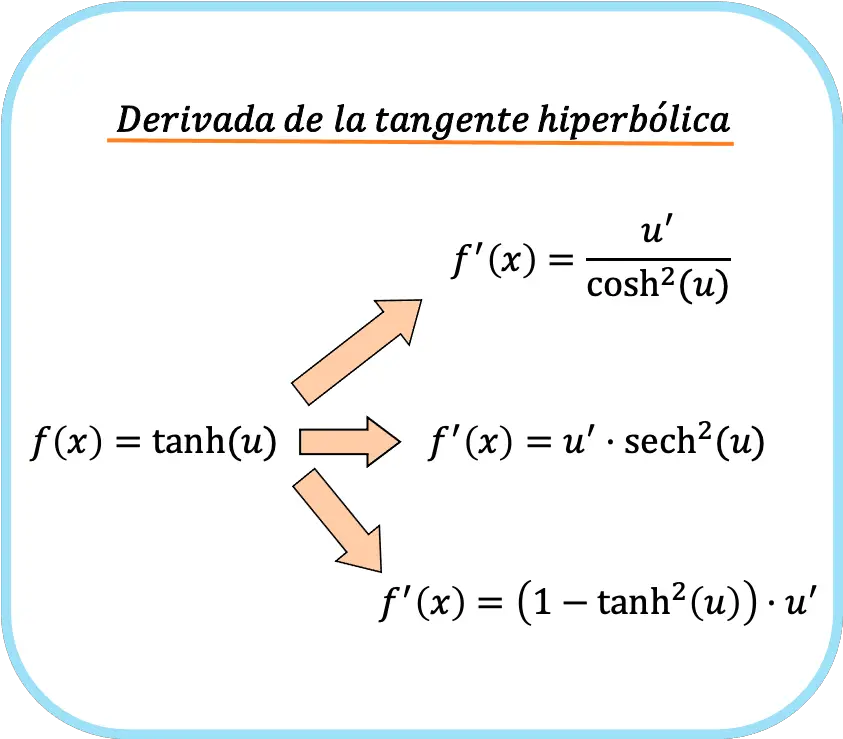
$\begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}$

これは、双曲線正接を導出するたびに 3 つの公式をすべて使用する必要があるという意味ではなく、いずれかを使用して双曲線正接を導出できるという意味です。したがって、双曲線正接引数の関数に応じて、ある式または別の式を使用する方がよいでしょう。以下に、関数の双曲線正接がどのように導出されるかを示すいくつかの例を示します。

双曲線正接の導関数

双曲線正接の導関数は接線の導関数とほぼ同じですが、細部が完全に異なります。違いは次のリンクで確認できます。

➤参照: 接線微分公式

双曲線正接の導関数の例

双曲線正接の導関数の公式を確認した後、双曲線正接の導出方法を完全に理解できるように、このタイプの三角関数の導関数の解決例をいくつか示します。

例 1: 2x の双曲線正接の導関数

$f(x)=\text{tanh}(2x)$

この例では双曲線正接を導出するために双曲線余弦の式を使用しますが、もちろん好きな方を使用できます。

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

2x の導関数は 2 であることがわかっているため、関数全体の導関数は次のようになります。

$f(x)=\text{tanh}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cosh}^2(2x)}$

例 2: x の 2 乗の双曲線正接の導関数

$f(x)=\text{tanh}(x^2)$

関数の双曲線正接の導関数の規則は次のとおりです。

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

一方で、関数を引数 x ²から微分すると、2x が得られ、次に次の公式を使用して関数全体の導関数を解きます。

$f(x)=\text{tanh}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cosh}^2(x^2)}$

例 3: 双曲線正接の 3 乗の導関数

$f(x)=\text{tanh}^3(7x^2)$

この場合、さらにべき乗された関数の双曲線正接を導出する必要があります。したがって、ポテンシャル関数の導関数の公式、双曲線正接の導関数の規則、および連鎖規則を使用する必要があります。

$f'(x)=3\text{tanh}^2(7x^2)\cdot \cfrac{14x}{\text{cosh}^2(7x^2)}}=\cfrac{42x\cdot \text{tanh}^2(7x^2)}{\text{cosh}^2(7x^2)}}$

接線の導関数の証明

このセクションでは、双曲線正接の導関数の公式を示します。そして、このために、3 つの双曲線三角比を接続する三角恒等式から始めます。

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

➤注:証明を理解するには、双曲線サインの導関数と双曲線余弦の導関数が何かを知る必要があります。したがって、続行する前にリンク先のページにアクセスすることをお勧めします。

ここで、商の導関数の公式を適用してみましょう。

$\displaystyle\left(\text{tanh}(x)\right)'=\left(\frac{\text{senh}(x)}{\text{cosh}(x)}\right)'$

$\text{tanh}'(x)=\cfrac{\text{cosh}(x)\cdot \text{cosh}(x)-\text{senh}(x)\text{senh}(x) }{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

次の式を使用して、分数の分子の式を簡略化します。

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

$\text{tanh}'(x)=\cfrac{1}{\text{cosh}^2(x)}$

ご覧のとおり、前の等式は双曲線正接の導関数の最初の式に対応します。同様に、双曲線正割は双曲線余弦の逆乗であるため、2 番目の式も導出されます。

$\text{tanh}'(x)=\text{sech}^2(x)$

最後に、前のステップの分数を分数の減算に変換することで、双曲線正接の導関数の 3 番目の規則に到達できます。

$\text{tan}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)}{\text{cosh}^2(x)}-\cfrac{\text{senh}^2(x)}{\text{cosh}^2(x)}$

$\text{tanh}'(x)=1-\text{tanh}^2(x)$

コメントする返信をキャンセル