ここでは関数の双曲線余接を求める方法を説明します。双曲線余接の導関数の例も見つかります。
双曲線余接の導関数の公式
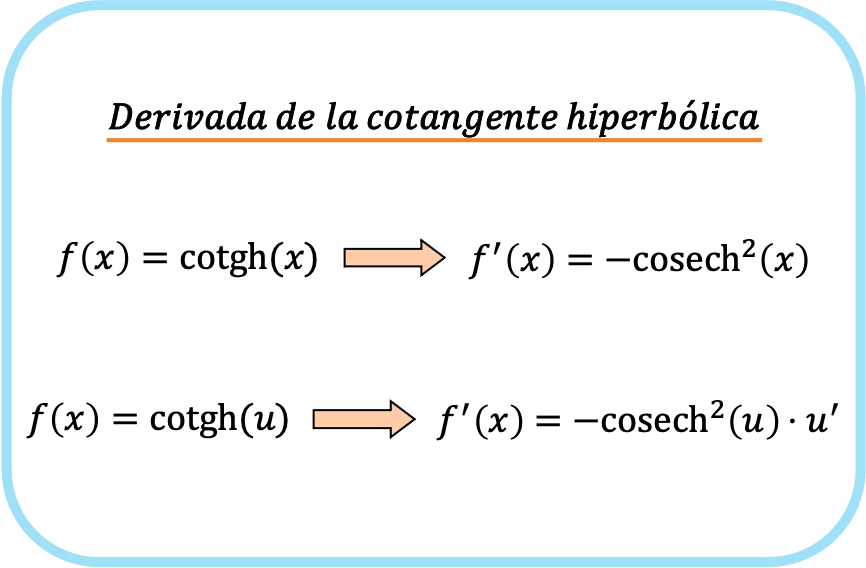
x の双曲線余接の導関数は、x の双曲線余割を 2 乗した値を引いたものに等しくなります。
![]()
したがって、関数の双曲線余接の導関数は、関数の双曲線余割を引いた値とその関数の導関数を乗算したものになります。
![]()
2 番目の式では連鎖規則が適用されており、この式は双曲線余接引数に x 以外の関数がある場合に使用されることに注意してください。
一部の数学の本では、次の 3 つの式は同等であるため、コタンジェントの導関数が別のものであると記載されている場合があります。
![]()
明らかに、双曲線余接を導出するために 3 つの式の中から好きな式を使用できますが、最もよく使用されるのは双曲線余割の 2 乗です。
双曲線余接の導関数の例
関数の双曲線余接の導関数の公式が何であるかを理解したら、このタイプの三角関数導関数のいくつかの例を解きます。
例1
この例では、関数 2x の双曲線余接の導関数が何であるかを見ていきます。
![]()
双曲線余接引数には x 以外の関数があるため、導出を行うには連鎖規則を備えた式を使用する必要があります。
![]()
2x は 1 次項であるため、その導関数は 2 です。したがって、2x の双曲線余接の導関数を求めるには、単に双曲線余割の 2 乗引数に 2x を入れて 2 を掛けます。
![]()
例 2
2 番目の例では、多項式関数の双曲線余接の導関数の値を決定します。
![]()
上で見たように、関数の双曲線余接を導出するルールは次のとおりです。
![]()
したがって、この演習の双曲線余接の導関数は次のようになります。
![]()