双曲線余弦関数

7月 4, 2023

ここでは、双曲線コサイン関数に関するすべてがわかります。その公式、グラフ表現、特性、他の関数との数学的関係などです。

双曲線余弦の公式

双曲線コサイン関数は主要な双曲線関数の 1 つであり、記号cosh(x)で表されます。双曲線余弦は、e ^xと e ^-xを足したものを 2 で割った値に等しくなります。

したがって、双曲線余弦の式は次のようになります。

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

したがって、双曲線余弦は数学的に指数関数に関連しています。次のリンクでは、このタイプの関数のプロパティを確認できます。

➤参照:指数関数の性質

双曲線余弦のグラフ表示

双曲線コサイン関数のグラフ表示は、二次関数 (または放物線) の形式になります。

双曲線余弦

➤「2 次関数のグラフ表示」を参照してください。

このグラフでは、双曲線余弦が y 軸に関して対称であるため、偶関数であることがはっきりとわかります。

一方、双曲線余弦のグラフは、周期関数である余弦（三角関数）のグラフとは大きく異なります。次のリンクで、コサインのグラフ表現と双曲線コサインとのすべての違いを確認できます。

➤参照:コサイン関数のグラフ表示

ハイパボリックコサインの特徴

双曲線余弦は次の特性を考慮します。

双曲線余弦関数の定義域はすべて実数です。

$\text{Dom } f = \mathbb{R}$

代わりに、双曲線余弦関数の範囲 (または範囲) は 1 であり、すべての数値は 1 より大きくなります。

$\text{Im } f= [1,+\infty)$

双曲線余弦は連続的で偶数の関数です。

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

関数は点 x=0 で Y 軸と交差します。

$(0,1)$

一方、関数には X 軸との交点がありません。

双曲線余弦関数の無限大に対する 2 つの制限 (正と負) により、プラスの無限大が得られます。

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

双曲線余弦は x = 0 まで減少し、その時点から無限に増加するため、関数は x = 0 で最小値になります。

$(0,1)$

この関数は領域全体で凸であるため、変曲点がありません。

双曲線余弦関数の導関数は双曲線正弦です。

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

双曲線余弦関数の積分は双曲線正弦です。

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

双曲線余弦関数のテイラー多項式 (またはマクローリン級数) は次のとおりです。

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

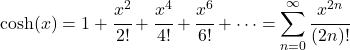
双曲線余弦関数のラプラス変換は次のとおりです。

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

双曲線余弦の数学的関係

次に、他の双曲線関数はすべて数学的に関連しているため、他の双曲線関数から双曲線余弦を計算する方法を見ていきます。

基本方程式は、双曲線余弦を双曲線正弦に関連付けます。

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤参照:双曲線正弦

3 つの主要な双曲線関数 (双曲線サイン、コサイン、およびタンジェント) は、次の方程式で関連付けられます。

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

一方、2 つの異なる数値の加算 (または減算) の双曲線余弦は、次の式で求めることができます。

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

数値を 2 倍した双曲線余弦は、この数値の双曲線余弦と双曲線正弦の二乗の和に等しくなります。

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

2 つの双曲線余弦の加算または減算は、次の式を適用して計算できます。

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

最後に、双曲線余弦の二乗は次の式で計算できます。

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

コメントする返信をキャンセル