双曲線余割の微分

この記事では、関数の双曲線コセカントを導出する方法を説明します。さらに、双曲線コセカントの導関数の解決例をいくつか見ることができます。

双曲線余割の導関数の公式

x の双曲線余割の導関数は、x の双曲線余割を引いた値と x の双曲線余接を掛けた値に等しくなります。

$f(x)=\text{cosech}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(x)\cdot \text{cotgh}(x)$

したがって、関数の双曲線余割の導関数は、関数の双曲線余割と関数の双曲線余接とその関数の導関数の積を引いたものになります。

$f(x)=\text{cosech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(u)\cdot \text{cotgh}(u)\cdot u'$

つまり、関数のコセカントを求める公式は次のとおりです。

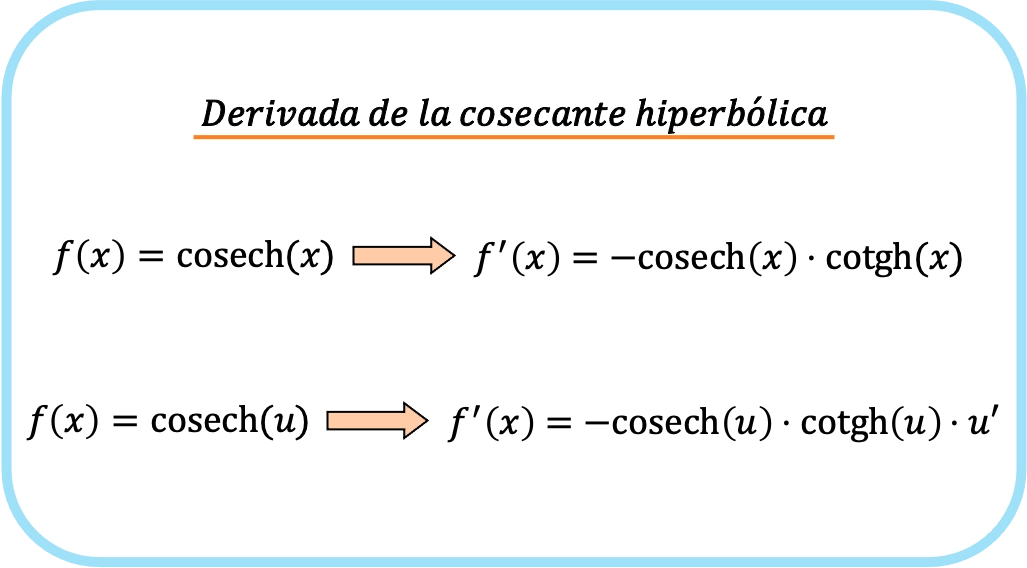
実際、前の 2 つの式は 1 つの式に対応します。違いは、連鎖ルールが 2 番目の式に適用されることです。

双曲線余割の導関数の公式が何であるかを確認した後、このタイプの三角関数導関数の実際の例をいくつか示します。

この最初の例では、x の 2 乗の双曲線余割を導出します。

$f(x)=\text{cosech}(x^2)$

双曲線余割の引数の関数は x とは異なるため、連鎖律による双曲線余割の導関数の公式を使用する必要があります。

$f(x)=\text{cosech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(u)\cdot \text{cotgh}(u)\cdot u'$

したがって、この三角関数を導出するには、前の式の値を代入するだけです。つまり、双曲線余割と双曲線正接の引数に x ²を代入し、そのすべてに導関数を乗算します。 x の 2 乗、つまり 2x:

$f(x)=\text{cosech}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(x^2)\cdot \text{cotgh}(x^2)\cdot 2x$

この演習では、x の 3 乗の双曲線余割の微分がどのくらいになるかを確認します。

$f(x)=\text{cosech}(x^3)$

関数の双曲線余割の導関数を求めるには、その公式を適用します。

$f(x)=\text{cosech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(u)\cdot \text{cotgh}(u)\cdot u'$

x の 3 乗の導関数は 3x ²であるため、関数全体の導関数は次のようになります。

$f(x)=\text{cosech}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(x^3)\cdot \text{cotgh}(x^3)\cdot 3x^2$