双曲線逆正弦導関数

ここでは、双曲線逆正弦の導関数 (公式) が何であるかを示します。さらに、関数の双曲線逆正弦の導関数について解決されるいくつかの演習を見ることができます。最後に、このタイプの三角関数の導関数の公式を示します。

双曲線逆正弦導関数の公式

x の双曲線逆正弦の導関数は、x の 2 乗の平方根に 1 を加えたものです。

f(x)=\text{arcsenh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2+1}}

したがって、関数の双曲線逆正弦の微分値は、その関数の微分値をその関数の平方根で割った商に 1 を加えたものに等しくなります。

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

2 番目の式は最初の式と似ていますが、連鎖規則を適用します。つまり、最初の式では xy の双曲線逆正弦のみを求めることができますが、第 2 の式では任意の関数の逆双曲線正弦を求めることができます。

双曲線逆正弦から導出

双曲線逆正弦は双曲線正弦の逆関数であることに注意してください。その導関数は次のようになります。

➤参照: 双曲線正弦の導関数の公式

双曲線逆正弦導関数の例

例1

f(x)=\text{arcsenh}(3x)

逆正弦関数の導関数を解くには、上記の公式を使用します。

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

3x の導関数は 3 なので、分子には 3 が入ります。そして、分母には 3x の 2 乗に 1 を加えた平方根を入力するだけです。

f(x)=\text{arcsenh}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{\sqrt{(3x)^2+1}}=\cfrac{3}{\sqrt{9x^2+1}}

例 2

f(x)=\text{arcsenh}(x^3)

関数 x 3 の双曲線逆正弦を導出するには、同じ公式を適用する必要があります。

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

x の 3 乗導関数は 3x 2なので、x の双曲線逆正弦の導関数を 3 乗したものは次のようになります。

f(x)=\text{arcsenh}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3x^2}{\sqrt{\left(x^3\right)^2+1}}=\cfrac{3x^2}{\sqrt{x^6+1}}

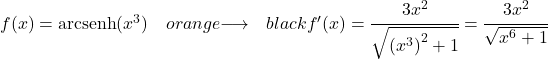
双曲線逆正弦導関数の証明

双曲線逆正弦の導関数の公式を示します。

y=\text{arcsenh}(x)

まず、双曲線逆正弦を双曲線正弦に変換します。

x=\text{senh}(y)

等式の両側から次のように推定します。

1=\text{cosh}(y)\cdot y'

私たちはあなたをクリアします：

y'=\cfrac{1}{\text{cosh}(y)}

次に、双曲線サインと双曲線余弦を接続する三角関数恒等式を適用します。

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{cosh}(y)=\sqrt{1+\text{senh}^2(y)}

y'=\cfrac{1}{\sqrt{1+\text{senh}^2(y)}}

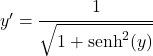
しかし、上で x が y の双曲線正弦に対応すると推論したため、方程式は残ります。

y'=\cfrac{1}{\sqrt{1+x^2}}

ご覧のとおり、これらの手順を適用することにより、双曲線逆正弦の導関数の公式が得られ、それが証明されたのです。

類似商品

コメントする

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

上部へスクロール