ここでは、双曲線とは何か、その特徴的な要素は何か、方程式の見つけ方、例、解決された演習など、双曲線に関するすべてを見つけることができます。
誇張とは何ですか?
双曲線は 2 つの分岐を持つ開いた曲線であり、その数学的定義は次のとおりです。
解析幾何学では、双曲線は次の条件を満たす平面上の点の軌跡です。双曲線の任意の点と 2 つの固定点 (焦点と呼ばれます) の間の距離の差の絶対値が一定でなければなりません。
さらに、これら 2 つの距離を減算した値は、常に双曲線の 2 つの頂点間の距離に等しくなります。
![]()

以下に係数が何を意味するかを見てみましょう
![]()
誇張の。
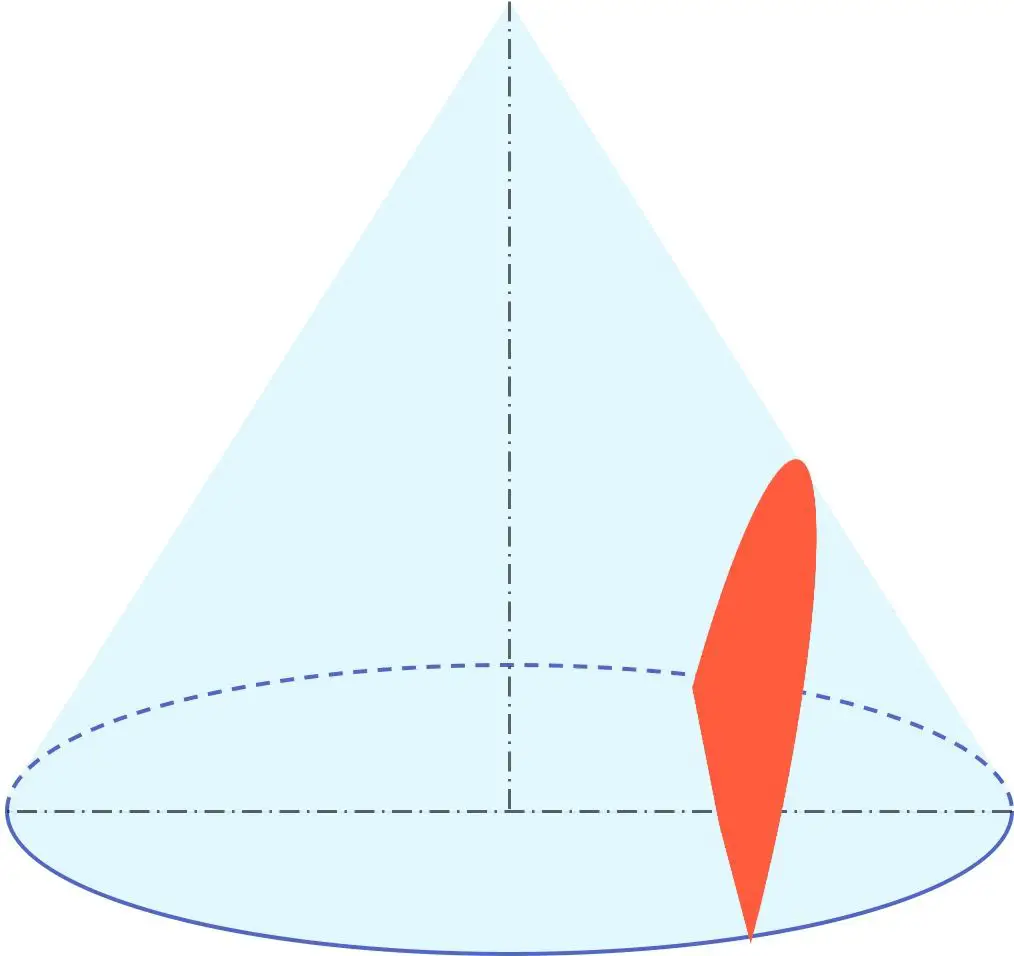
さらに、双曲線は、円周、楕円、放物線とともに円錐と呼ばれる幾何学的グループの一部です。したがって、双曲線は円錐断面、つまり円錐から得られます。
特に、双曲線は、回転軸に対して円錐の生成部によって形成される角度より小さい角度を有する平面による円錐の断面の結果である。
双曲線の要素
双曲線の特性は以下によって異なります。
- 焦点: これらは、各双曲線に特徴的な 2 つの固定点です (下のグラフの点 F および F’)。双曲線の任意の点から各焦点までの距離の差の絶対値は一定であり、以下に等しい。

- 焦点軸または主軸: 双曲線の 2 つの焦点を通過する線です。それは、前記幾何学的図形の対称軸に対応する。横軸または横軸とも呼ばれます。
- 二次軸: セグメント FF’ の二等分線 (点 B と B’ を通過する線) です。また、焦点軸に垂直な線であり、双曲線のもう一つの対称軸でもあります。
- 中心 (O) : 2 つの軸の交点、および 2 つの頂点と 2 つの焦点の中点です。双曲線には 2 つの対称軸があるため、対称の中心でもあります。
- 頂点 (A および A’) : 双曲線の枝と焦点軸との交点です。
- ベクトル光線 (R) : これらは、双曲線上の任意の点から各焦点に向かうセグメントです。
- 焦点距離: 2 つの焦点間の複合セグメントの長さです。
- 長軸または実軸:点 A から点 A’ までの線分であり、その長さは以下に相当します。

- 小軸または虚軸:点 B から点 B’ までの線分であり、その長さは以下に相当します。
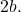
- 漸近線: グラフに示されている点線です。それらがどのように計算されるかを以下で見てみましょう。
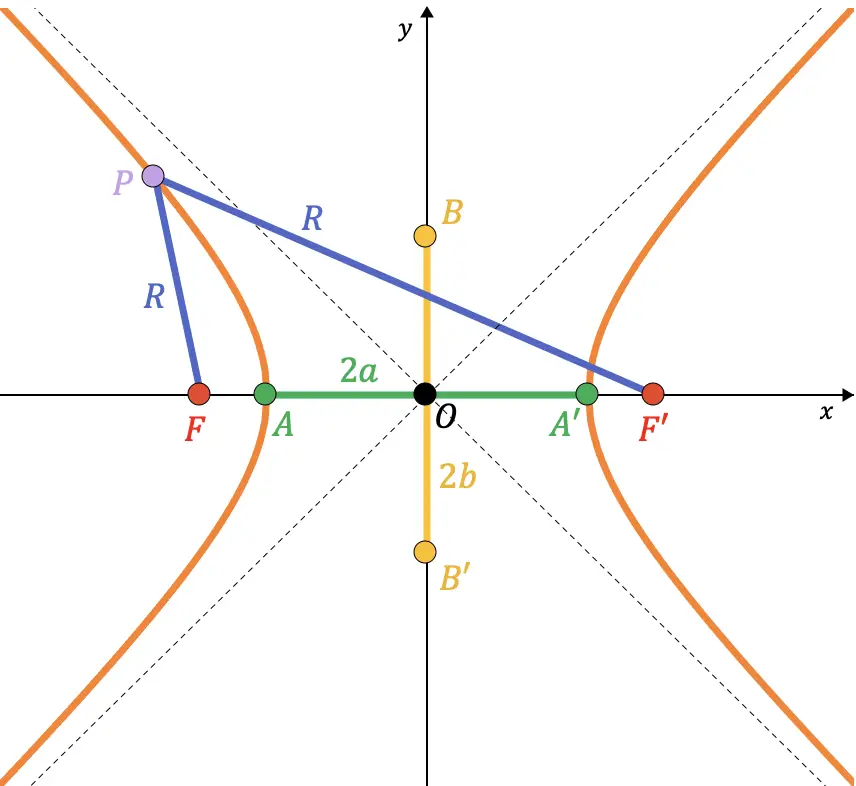
双曲線の要素間の関係
まず、半軸とは軸の半分という意味です。たとえば、真の半軸は、点 A から双曲線の中心まで向かう線分であり、その長さは
![]()
したがって、実半軸、虚半軸、および半焦点距離の間には非常に重要な関係がある。実際、次に導出する公式は、双曲線の演習や問題を解くためによく使用されます。
双曲線の点 B と B’ は、主軸と仮想半径円の交点に対応することを知っておく必要があります。
![]()
したがって、次の図でわかるように、点 A と点 B を結ぶ線分は、前記円の半径 (
![]()
):
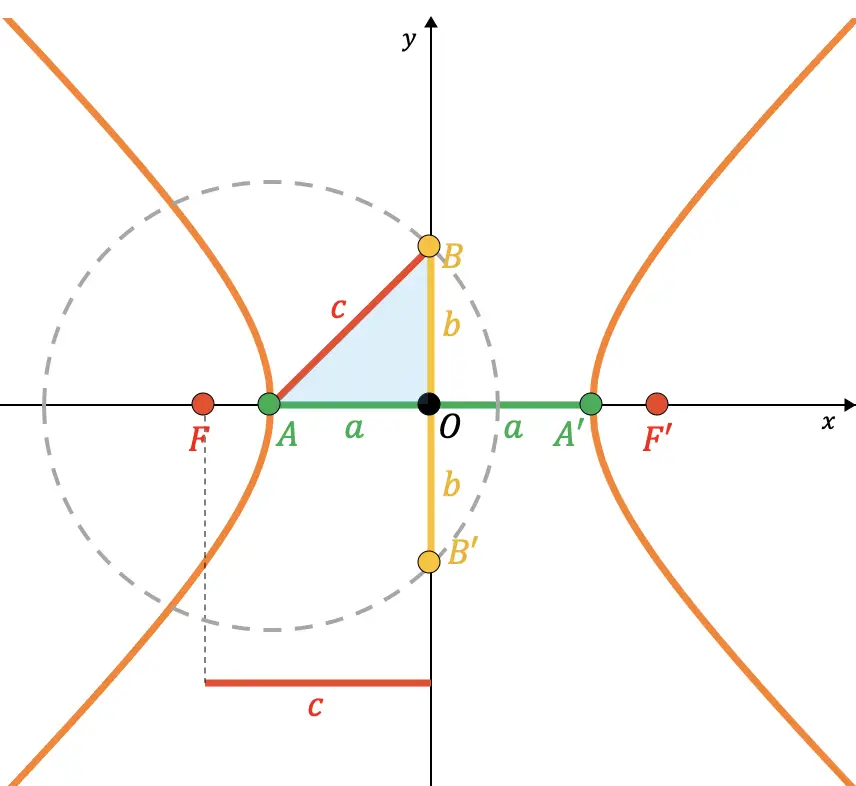
したがって、ピタゴラスの定理から、パラメータ間の関係が次のように証明できます。
![]()
そして
![]()
は次のとおりです。
![]()
双曲線方程式
双曲線方程式にはいくつかの種類があり、その特性に応じてどちらかが数学的に表現されるために使用されます。次に、それぞれを詳しく分析していきます。
まず、双曲線の常方程式があります。次に、常方程式の変形を見ていきます。これは、双曲線の縮小方程式または正準方程式です。次に、双曲線の一般方程式がどのようなものであるかを学習します。そして最後に、双曲線の 2 つの特殊なケース、つまり等辺双曲線と共役双曲線の方程式を分析します。
双曲線の常方程式
座標の原点 (点 (0,0)) に外部中心がある双曲線を方程式で定義したい場合は、次の公式を使用する必要があります。
デカルト座標における双曲線の常方程式の公式は次のとおりです。
![]()
金:
-

そして

は双曲線の中心の座標です。
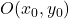
-

は双曲線の長半径の長さです。
-

双曲線の短半径の長さです。
この方程式を使用すると、焦点軸が水平 (枝が左右に開く) の双曲線を記述することができます。これが通常の双曲線です。しかし、垂直焦点軸 (枝が上から下に開く) を扱う場合、負の符号は変数 y から変数xに渡されます。
![]()
金
![]()
そして
![]()
は、前と同様、双曲線の中心の座標と項です。
![]()
そして
![]()
これらは依然として双曲線の長半径と短半径ですが、以前とは異なり、これら 2 つはそれぞれ垂直方向と水平方向を向くようになります。
双曲線の正準方程式または縮小方程式
このタイプの双曲線方程式は常方程式に非常に似ていますが、唯一の違いは、点 (0,0) を中心とする双曲線を解析的に表現するために正準方程式が使用されることです。したがって、双曲線の中心が座標の原点である場合、双曲線の正準方程式または縮小方程式を使用します。
ここで、常方程式から双曲線の縮小方程式の公式を導き出します。
![]()
双曲線の中心が座標の原点、つまり点 (0,0) である必要がある場合、次のことが常に当てはまります。
![]()
![]()
したがって、双曲線の正準方程式または縮小方程式は次のようになります。
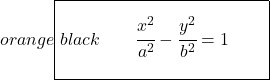
前と同様、焦点軸が水平ではなく垂直の場合、負の変数はxになります。
![]()
双曲線の一般方程式
双曲線の一般方程式の式は次のとおりです。
![]()
ただし、上の方程式が双曲線になるためには、係数は次のようになります。
![]()
そして
![]()
それらはゼロとは異なり、同時に反対の符号を持たなければなりません。
正双曲線方程式
等辺双曲線は、実半軸の長さが虚半軸の長さに等しい双曲線です。これは、次のことを意味します。
![]()
したがって、等辺双曲線の方程式は次のようになります。
![]()
さらに、等辺双曲線の漸近線は互いに垂直です。これらの直線の方程式は次のとおりです。
![]()
![]()
よく見ると、これら 2 つの方程式はそれぞれ、第 1 象限 (および第 3 象限) と第 2 象限 (および第 4 象限) の二等分線です。したがって、等辺双曲線を左に 45 度回転すると、その漸近線が座標軸の位置を占めます。
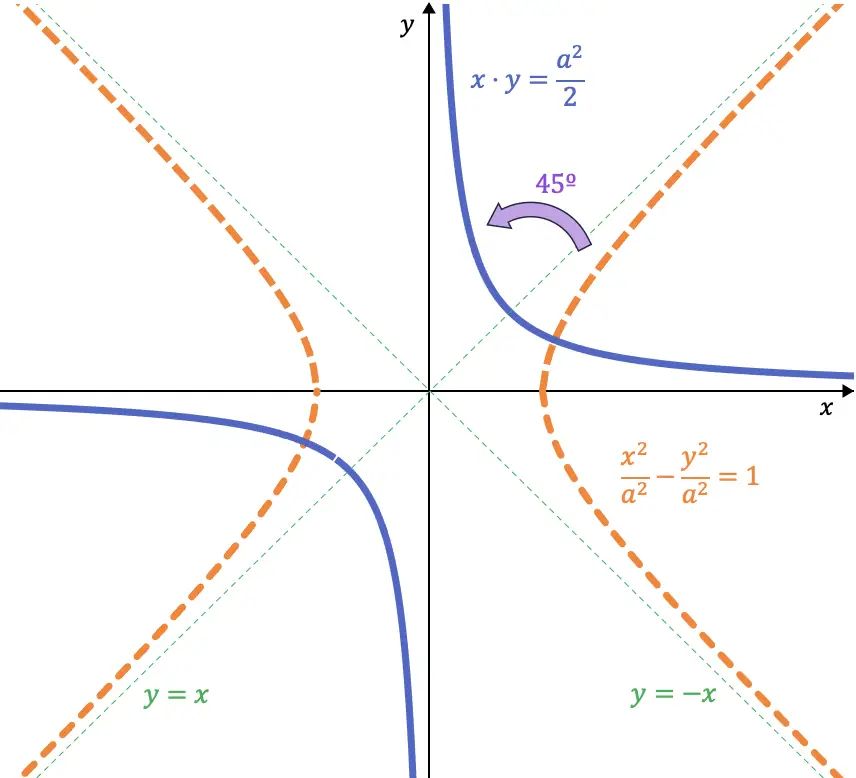
したがって、45 度回転するときの双曲線の方程式は次のようになります。
![]()
共役双曲線
2 つの双曲線は、一方の実軸が他方の虚軸と等しい場合に共役になります。したがって、分母の係数は同じままでなければならないため、2 つの共役双曲線の方程式の唯一の違いは、どの変数が否定されるかということです。
以下は、互いに共役な 2 つの双曲線の方程式の例です。
![]()
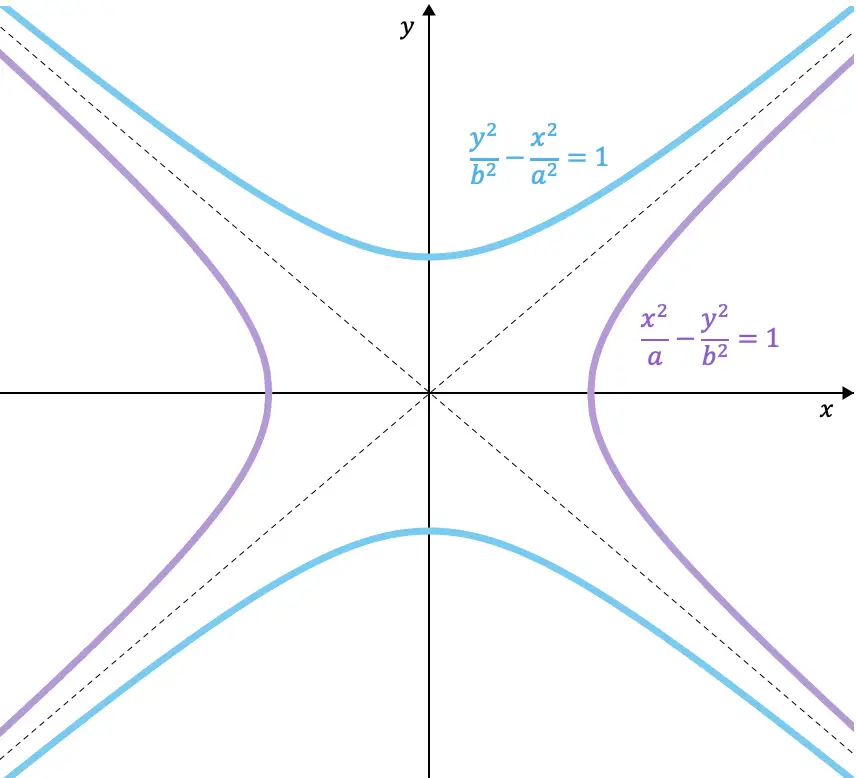
さらに、グラフ化された双曲線からわかるように、共役双曲線は同じ漸近線を共有します。
双曲線の漸近線
前のグラフで見たように、各双曲線には 2 つの漸近線があります。漸近線とは関数に非常に近づく直線ですが、完全に交差したり接触したりすることはないことに注意してください。
したがって、双曲線の漸近線に対応する式は次のとおりです。
![]()
![]()
双曲線の漸近線をその係数を使用して簡単に決定できるようにする
![]()
そして
![]()
これらはそれぞれ、双曲線の実半軸と虚半軸の長さです。
双曲線の離心率
双曲線の離心率は、双曲線の開き具合または閉じ具合を決定する特性パラメータです。数値的には、双曲線の離心率は、その半焦点長をその実半軸で割ることによって計算されます。
![]()
双曲線の離心率は常に 1 より大きくなります。
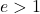
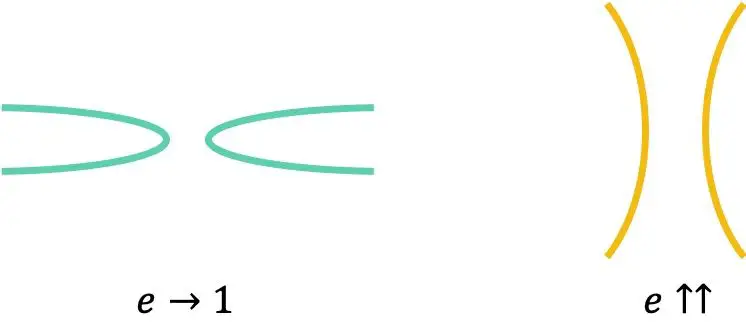
最後に、等辺双曲線の離心率は常に次と等しいことに注意してください。
![]()
双曲線の問題が解決されました
以下では、双曲線と双曲線方程式の問題や解いた演習で見てきた概念を練習することができます。
演習 1
点 (-1.3) を中心とし、実半軸の長さが 3 単位、虚半軸 (Y 軸に平行) の長さが 7 単位である双曲線の方程式は何ですか?
双曲線の方程式を見つけるには、単に双曲線の常方程式の公式を適用するだけです。
![]()
双曲線の中心の座標を方程式に代入します。
![]()
![]()
そして最後に、未知数の値を代入します
![]()
そして
![]()
![]()
![]()
演習 2
方程式が次のように定義される双曲線の中心、頂点、焦点、離心率の値、漸近線の座標を求めます。
![]()
まず、方程式の負の変数は変数yであることに注意してください。そのため、双曲線の枝は左右に開きます (焦点軸が X 軸に平行)。
第 2 に、方程式は双曲線の正準 (または縮小) 方程式に対応するため、その中心が座標の原点になります。
![]()
双曲線の中心がわかったら、他のすべてを計算するために実際の半軸の値 (パラメータ) を見つける必要があります。
![]()
) と仮想の半軸 (パラメータ
![]()
)。双曲線の正準 (または縮小) 方程式の式から両方を推定できます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
したがって、中心と頂点の間に 5 単位の距離がある場合、これは双曲線の頂点が次のとおりであることを意味します。
![]()
各焦点の座標を決定するには、焦点距離の半分の値 (パラメータ
![]()
)。このために、双曲線の要素を接続する公式を使用できます。
![]()
![]()
![]()
したがって、センターとホームの間には 13 ユニット分のスペースがあります。したがって、各世帯の座標は次のようになります。
![]()
次に、双曲線の離心率を計算するには、対応する公式を使用する必要があります。
![]()
そして最後に、双曲線の漸近線とその公式を見つけます。
![]()
![]()
演習 3
双曲線の点から焦点 F(-4.0) と F(4.0) までの距離の差が 6 単位であることを知って、座標の原点を中心とする双曲線の方程式を計算します。
まず、双曲線の中心は座標の原点にあるため、正準方程式または縮小方程式を使用します。
![]()
次に、双曲線の定義によれば、その点の 1 つから焦点までの距離の差の絶対値 (この場合は 6) は、実軸の長さに等しくなければなりません (
![]()
)。まだ:
![]()
![]()
![]()
![]()
一方、双曲線の中心は点(0,0)であり、焦点は点(4,0)である。したがって、2 点までの距離 (パラメータ)
![]()
)は4単位です。
![]()
これでパラメータの値が分かるようになりました
![]()
双曲線の 3 つの特性係数間の数学的関係は次のようになります。
![]()
![]()
![]()
![]()
したがって、双曲線の方程式は次のようになります。
![]()
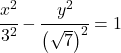
![]()