この記事では、無限マイナス無限(∞-∞)の不確定性を解く方法を説明します。さまざまなタイプの関数を使用したこの不確定性の例が見つかり、さらに、不確定性の無限マイナス無限を段階的に解く練習問題を練習することができます。
無限マイナス無限を解く不確定性
関数の極限が無限大マイナス無限大となる場合、それは不確定性(または不確定形式)であることを意味します。つまり、不定性マイナス無限大を与える関数の極限は、直接計算を実行することによって決定することはできず、むしろ予備的な手順を実行する必要がある。
したがって、無限マイナス無限の不確定性を解決するには、まず関数の種類に応じた手順を適用する必要があります。多項式関数の場合は比較によって計算でき、有理関数の場合は分数を次のように換算する必要があります。共通の分母であり、それが無理関数である場合は、共役を乗算する必要があります。
![]()
次に、無限マイナス無限の不定性が各タイプの関数でどのように解決されるかを例を使って見ていきます。
多項式関数における無限マイナス無限の不確定性
多項式では、不確定性無限大から無限大を引いたものが最高次数の無限大と等しくなります。つまり、最高次数の項が無限大の正負の符号を決定します。
たとえば、無限形式から無限大を引いた不定形を与える次の多項式関数の極限を見てください。
![]()
この場合、項 x 2は 2 次であり、項 3x は 1 次であるため、単項式 x 2は高次であるため支配的です。したがって、この項から得られる極限の結果は無限大となります。
以下の他の例を見てください。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bfb5cd294a19de382f74738af6be724_l3.png)
つまり、多項式関数で無限を制限する場合は、他のすべての項を無視して、単純に無限を最高次項に代入する必要があります。
分数を伴う不確定性無限マイナス無限
代数分数の加算または減算で無限大マイナス無限大の不確定性が発生する場合、最初に分数の加算または減算を行ってから、極限を計算する必要があります。
例を段階的に解決して、分数を含む関数の不確定性無限大マイナス無限大を計算する方法を見てみましょう。
![]()
まず制限を計算してみましょう。
![]()
しかし、不確定性 ∞-∞ が得られます。
したがって、最初に分数の引き算を行う必要があります。これを行うには、分数を共通の分母に換算します。つまり、一方の分数の分子と分母に、もう一方の分数の分母を掛けます。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68e489c5833478cb20929ea07ae2971d_l3.png)
両方の分数の分母が同じになったので、これらを 1 つの分数に結合できます。
![]()
分子と分母で演算します。
![]()
そして最後に、制限を再度計算します。
![]()
この場合、分子の次数が分母の次数よりも大きいため、無限大間の無限不確定性は + ∞ を与えます。
➤参照: 無限の間の無限とは何ですか?
不確定性無限マイナス無限根付き
根号加算または根号減算で無限大マイナス無限大の不確定性が発生する場合、まず共役根号式で関数を乗算および除算してから、極限を解く必要があります。
ステップバイステップの例を使用して、無理関数の不確定性無限マイナス無限を解決する方法を見ていきます。
![]()
まず、根号を使用して関数の極限を解いてみます。
![]()
ただし、不定形 ∞-∞ が得られます。したがって、無限大から無限大を引いた不確定性がどの程度かを知るには、説明した手順を適用する必要があります。
関数には根号があるため、共役無理数式で関数全体を乗算および除算します。
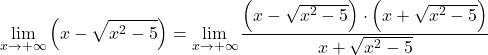
分子の代数式は、和と差の積の注目すべき単位に対応するため、式を簡略化できます。
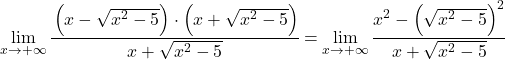
限界の根は二乗されるので、これを単純化します。
![]()
分数の分子を演算します。
![]()
![]()
そして最後に、制限の計算をやり直します。
![]()
したがって、無限大で割った数値はゼロに等しいため、制限の結果は 0 になります。
無限マイナス無限の不確定問題を解決しました
演習 1
x がプラス無限大に近づくにつれて、次の極限を解きます。
![]()
この極限では、最高次項は 3 次であるため、この項から得られる無限大に焦点を当てます。
![]()
演習 2
x が負の無限大に近づくときの次の多項式関数の極限を計算します。
![]()
負の無限大の 3 乗は負のままですが、2 乗すると正になります。後で、それらの符号はその前の係数によって変更されますが、次のようになります。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-172f2927f65e61079b13abd02234f1c7_l3.png)
次に、不定形式の無限大マイナス無限大は、最も高い次数の項 (-5x 3 ) によって定義され、そこから正の無限大が得られます。
![]()
演習 3
次の有理関数の無限大の極限を決定します。
![]()
まず、関数内の無限大を置き換えて制限を計算してみます。
![]()
しかし、最終的には ∞ – ∞ という不確定性が生じます。したがって、分数を共通の分母に換算します。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e2820674bc86d085f6deec7fdf9adf8_l3.png)
そして、両方の分数の分母が同じになったので、それらを 1 つの分数に結合できます。
![]()
分子のかっこを作ります。
![]()
そして最後に、制限を決定します。
![]()
この場合、分子の次数が分母の次数よりも大きいため、不決定 ∞/∞ は +∞ を与えます。
演習 4
x が 0 に近づくにつれて、次の分数関数の極限を解きます。
![]()
まず、いつものように制限を計算してみます。
![]()
しかし、不定形 ∞-∞ が得られます。したがって、関数の分数を共通の分母に減らす必要があります。
この場合、 x 4は x 2の倍数であるため、2 番目の分数の分子と分母に x 2を掛けるだけで、両方の分数が同じ分母を持つことがわかります。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-876115dc1fb49e81373d70be5fdcfb5e_l3.png)
2 つの分数を引き算できるようになりました。
![]()
もう一度制限を解決してみます。
![]()
しかし、最終的には定数をゼロで割った不確定性が生じます。したがって、関数の横方向の限界を計算する必要があります。
![]()
![]()
結論として、点 x=0 における関数の 2 つの横方向の極限は -∞ を与えるため、極限の解は -∞ になります。
![]()
演習 5
次の関数の無限極限を根で解きます。
![]()
極限を解こうとすると、無限マイナス無限という不確定性が得られます。
![]()
したがって、関数には根号があるため、共役根号式で乗算および除算する必要があります。
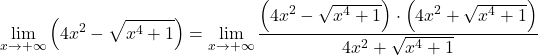
分子には、和と差の注目すべき積があり、これは二乗の差に等しいです。まだ:
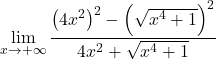
根号を二乗に単純化します。
![]()
分子で演算します。
![]()
![]()
そして最後に、限界を見つけます。
![]()
この場合、分子の次数が分母の次数よりも大きいため、無限不確定性を無限で割った値はより無限になります (平方根によって次数が 2 減少することを思い出してください:
![]()
)。
演習 6
次の無理関数の x が無限大に近づくときの極限を解きます。
![]()
まず、いつものように制限を計算してみます。
![]()
しかし、それは結果として、無限大の差が不定になることを与えます。したがって、関数にはルートがあるため、式を共役根号で乗算して除算する必要があります。
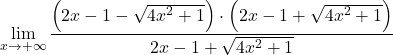
分数の分子の注目すべき等価性をグループ化します。
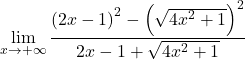
平方根を解きます。
![]()
差の二乗の注目すべき恒等式を解決します。
![]()
分子で演算します。
![]()
![]()
そして最後に、無限大での制限値を計算します。
![]()
分母に x の 2 乗がありますが、根の中にあるため、その次数は実際には 1 です。
![]()
したがって、分子の次数は分母の次数と同じであるため、不確定性 -∞/+∞ の結果は、より高い次数の x の係数の除算になります。
![]()
分母に 2 つの 1 次項があることに注意してください。
![]()
そして
![]()
、不確定性 -∞/+∞ を解決するには、1 次項のすべての係数を取得する必要があります。
![]()
の
![]()
そしてその
![]()
の
![]()
演習 7
分数を使用して、x が次の関数の 1 に近づくときの極限を計算します。
![]()
制限を作成しようとすると、無限から無限を引いた不定の制限が得られます。
![]()
したがって、分数を共通の分母に減らす必要があります。つまり、一方の分数の分子と分母に、もう一方の分数の分母を乗算する必要があります。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-75bf3ffa177f32711c5509ce5fe5992d_l3.png)
そして、2 つの分数の分母が同じになったので、これらをまとめることができます。
![]()
私たちは以下を運営しています:
![]()
![]()
そして、もう一度制限を解いてみます。
![]()
しかし、不確定性ゼロがゼロで除算されることがわかります。したがって、分子多項式と分母多項式を因数分解する必要があります。
![]()
ここで、分子と分母で繰り返される因数を削除して分数を単純化します。
![]()
そして最後に、制限を解決します。
![]()