このページでは、三角行列とは何か、さまざまな種類の三角行列を例とともに示します。さらに、三角行列の行列式を計算する方法と、この非常に興味深い行列の性質についても説明します。最後に、三角行列に関連する行列であるヘッセンベルグ行列とは何かについても説明します。
三角行列とは何ですか?
三角行列の定義:
三角行列は、主対角線の上下のすべての要素がゼロ (0) である正方行列です。
三角行列は、すべての位置に 0 以外の要素を持つ行列よりも、三角行列の逆行列、行列式の計算、さらには連立一次方程式の解法さえもこのタイプの行列で解く方がはるかに簡単であるため、線形代数の計算で広く使用されています。 。
上三角行列
上三角行列は、主対角線より下の要素がゼロ (0) である正方行列です。
上三角行列の例:

下三角行列
下三角行列は、主対角より上の各要素にゼロ (0) を持つ正方行列です。
下三角行列の例:
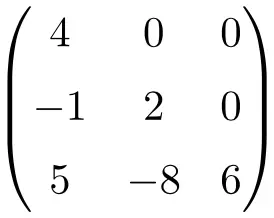
これらの行列は、上三角行列を表す文字 U を使用して、下三角行列を表す文字 L を使用して呼ばれることもあります。この命名法は主に英語で使用されていますが、実際には、U は上三角行列、L は下三角行列を表します。
三角行列の例
2×2次元三角行列
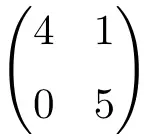
3×3次の三角行列
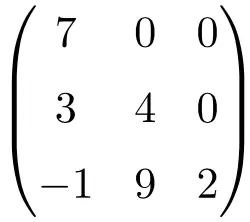
サイズ 4×4 の三角行列

三角行列の行列式
三角行列の行列式は、上三角であろうと下三角であろうと、主対角要素の積です。
行列式を見つけるには、三角行列の主対角要素の乗算を計算するだけで十分であることを解決する次の演習を見てください。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7503e88c4eaabd74347a4f79461a3ebe_l3.png)
この定理は簡単に証明できます。ブロック (または余因子) によって三角行列の行列式を計算するだけです。このデモは、一般的な三角行列を使用して以下で詳しく説明されています。
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-91281c322af35f07cfbfd6fe61fc3c58_l3.png)
一方、行列式が 0 以外の場合、行列は可逆であることがわかっています。したがって、主対角要素が 0 でない場合、三角行列も可逆となり、その結果、正規行列になります。マトリックス。
三角行列の性質
ここで、三角行列のプロパティを見てみましょう。
- 2 つの上三角行列の積は、 1 つの上三角行列と等しくなります。逆も同様です。2 つの下三角行列を乗算すると、別の下三角行列が得られます。
![Rendered by QuickLaTeX.com \begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dfd46e0ab8070d1c4c544d384fcf0f84_l3.png)
- 上三角行列の転置は下三角行列であり、その逆も同様です。下三角行列の転置は上三角行列です。
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ca1b4a07e3136aa75d1a8026e5e7c1ae_l3.png)
- 三角行列は、主対角上のすべての要素が非ゼロの場合、つまり、それらがゼロとは異なる場合、可逆です。このような場合、上(下)三角行列の逆行列も上(下)三角行列になります。
![Rendered by QuickLaTeX.com \left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-adafaa535a161d29c9bcb8a31a572dc2_l3.png)
さらに、反転行列の主対角には、常に元の三角行列の主対角の要素の逆数が含まれます。
- 対角行列はすべて、上三角行列と下三角行列の両方です。次に例を示します。
![Rendered by QuickLaTeX.com \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-497726e030cc2af2c07b16fdf3544024_l3.png)
- したがって、スカラー行列は上三角行列でもあり、下三角行列でもあります。たとえば単位行列は次のようになります。
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e4e9931fb7ae104414006cee93978a7_l3.png)
- 主対角線の上下の要素が 0 であるため、明らかに、ゼロ行列は上三角行列でもあり、下三角行列でもあります。
![Rendered by QuickLaTeX.com \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb061dcbc869eba51ece12af43f796f_l3.png)
- 三角行列の固有値 (または固有値) は主対角要素です。
![Rendered by QuickLaTeX.com \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5](https://mathority.org/wp-content/ql-cache/quicklatex.com-272d0e156e1f27c20348b171c984e390_l3.png)
- 上三角行列または下三角行列は常に固有ベクトルに基づいて対角化できます。
- 任意の行列は、下三角行列と上三角行列の積に因数分解できます。つまり、任意の行列を三角行列乗算に変換できます。さらに、行列が可逆である場合、この変換は一意です。行列を因数分解するには、LU 分解法がよく使用されます。
行列を三角化する
基数を変更することで三角形化できる行列に関する定理がいくつかあります。ただし、ここでは、ガウス法の場合のように、線に基本変換を適用することによって行列を三角測量する方法を見ていきます。
例えば:
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f66a4f370b37168439de204c1b0b401c_l3.png)
このようにして、元の行列をすでに三角化しています。
ガウス法の行間で許可される基本的な変換は次のとおりであることを思い出してください。
- ある行を他の行の線形結合に置き換えます。
- 行内のすべての項を 0 以外の数値で乗算または除算します。
- 注文明細行を編集します。
ヘッセンベルグ行列
ヘッセンベルグ行列の定義は次のとおりです。
ヘッセンベルグ行列は「ほぼ」三角行列です。つまり、最初の下対角 (上ヘッセンベルグ行列) または最初の上対角 (下ヘッセンベルグ行列) から始まるすべての要素がゼロになります。
上側のヘッセンベルグ行列の例と下側のヘッセンベルグ行列の例を見ると最もよく理解できると思います。
上部ヘッセンベルグ行列
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e76ad0fae8a28b5e5f31535683e63df5_l3.png)
下部ヘッセンベルグ行列
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9b13730483eaf930193baeb953d1d3c_l3.png)
上ヘッセンベルグ行列と下ヘッセンベルグ行列の両方である行列は、三重対角行列です。
この行列は、20 世紀の著名なドイツのエンジニア兼数学者であるカール ヘッセンベルクにちなんで名付けられました。
最後に、このタイプの行列には、三角行列を乗算すると、結果が常にヘッセンベルグ行列になるという特殊性があります。