角度の三角比は、直角三角形の 3 つの辺から得られる比です。つまり、その三辺を商(割り算)で比較した結果の値です。ただし、これらの理由は直角三角形(角度が 90 度の三角形)にのみ存在することに注意してください。
直角三角形の三角比
最も重要な 6 つの三角比は、サイン、コサイン、タンジェント、コセカント、セカント、コタンジェントです。次に、これらのそれぞれの理由がどのように定義されるかについて詳しく説明し、それらを特徴付ける式について説明します。以下の説明を理解するために、次の直角三角形を考慮します。

胸
角度の正弦 (sin または sin) は、斜辺 (c) 間の反対側の脚 (a) の商に等しいため、正弦の公式は次のようになります: sin (α) = a / c 。サインの定義を知ることは非常に重要です。サインはすべての三角法の基礎であり、このセクションで説明する他の理由も同様です。
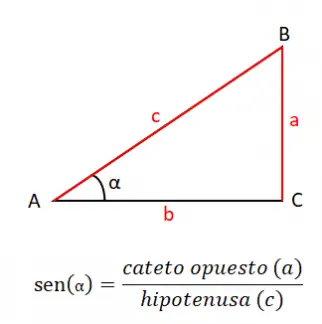
トラヴこれは正弦定理に基づいており、三角形の任意の辺を計算できます。これは、対応する辺間の特定の角度の商を接続することによって実行できます。たとえば、辺 a を計算する必要があり、角度 A と B による辺の値がある場合、次の式を使用して計算できます: a / sin (A) = b / sin (B) 。この単純な方程式を解くことで、計算したい変数に対応する値が得られます。
余弦
角度の余弦 (cos) は斜辺 (c) 間の隣接する脚 (b) の商に等しいため、余弦の公式はcos (α) = b / cとなります。この場合、式は、調査したい角度 (この例では角度 A または α) に接する三角形の 2 つの辺で構成されます。
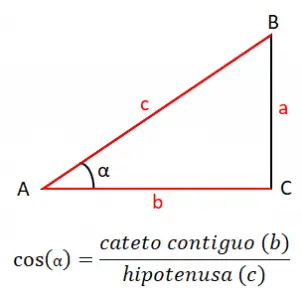
コサインを使用すると、コサイン定理に基づいて三角形の辺を計算する方法もあります。これにより、辺を角に接続できるようになり、次の 3 つの式が得られます。
a² = b² + c² – 2bc cos (A)
b² = a² + c² – 2ac cos (B)
c² = a² + b² – 2ab cos (C)
正接
3 番目に重要な理由は、これで一連の元の理由を終了することになりますが、タンジェント (tan または tg) です。これは、反対側の脚 (a) と隣接する脚 (b) の間で除算することによって計算されるため、接線の公式は次のようになります: Tan (α) = a / b 。以下にグラフで見ることができます。
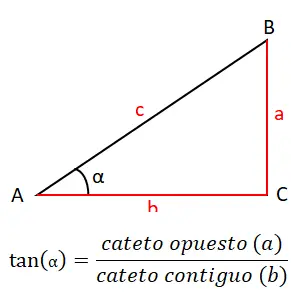
タンジェントには、タンジェント定理と呼ばれる独自の定理もあります。これにより、三角形の 2 つの辺の長さを角度の接線と関連付けることができます。ステートメントは次のとおりです。「2 つの辺の減算の商は、これらの辺に対向する 2 つの角度の平均の正接と、それらの差の半分の正接との商に等しい。」
三角比の導出
今説明した 3 つの三角比から、他の導出三角比を得ることができます。これらは、サイン、コサイン、タンジェントの逆比をとることで得られます。
- コセカント:サインの逆比であり、次の式で計算されます: cosec (α) = c / a および cosec (α) = 1 / sin (α)。
- セカント:コサインの逆比で、次の式で計算されます: sec (α) = c / b および sec (α) = 1 / cos (α)。
- コタンジェント:タンジェントの逆比で、公式: cotg (α) = b / a および cotg (α) = 1 / Tan (α) で計算されます。
三角比表
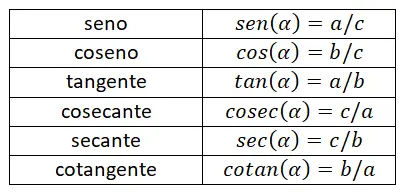
以下に、これまで説明したすべての理由をまとめた表を示します。この表を使用すると、各数式の違いを簡単に区別できるため、すべての公式を効果的に覚えることができます。
円の中の三角比
三角法を研究するもう 1 つの方法は、ゴニオメトリック円周または単位円を使用することです。この円周の半径は 1 で、原点は点 (0, 0) です。この図は円とその円の内側に描かれた直角三角形で構成されており、より正確には、これから研究する角度が原点に触れなければなりません。
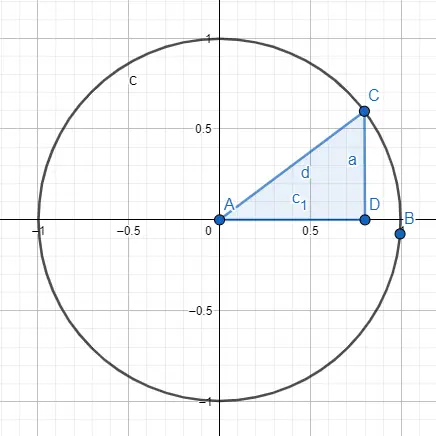
この画像があるとき、半径が斜辺に等しい、つまり 1 に等しいことがわかります。したがって、サインとコサインを計算したい場合は、半径の値と、その反対側の値を使用します。三角形。サインを計算するには、次の計算を行います: sin (A) = CD / AC = CD / radius = CD / 1 = CDしたがって、A のサインは a です。一方、コサインを計算するには、 cos (A) = AD / AC = AD / radius = AD / 1 = AD という計算を行います。したがって、A のコサインは c1 です。
2 つのことに留意することが非常に重要です。 1 つ目は、三角比の研究でこの円が使用されるのは、三角形で研究できる角度よりも大きな角度を扱う必要があるためです。たとえば、150 度の角度は大きすぎるため、単純な三角形では調べることができません。 2 番目に留意すべきことは、サインとコサインは 1 より大きく -1 より小さい値を決して採用できないということです。
三角比の符号
前に述べたように、三角形で処理できるより大きな角度を処理するには、ゴニオメトリック円周を使用します。これを行うには、円周を分割する4 つの象限の 1 つで、円の内側の三角形を正確に表します。次の図では、4 つの象限が表されていることがわかります。
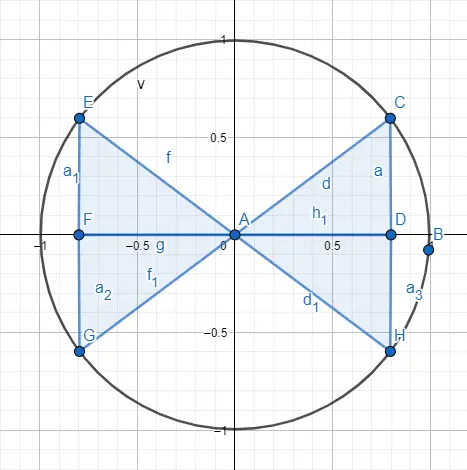
したがって、同じになる 30 の角度と 210 の角度を区別するには三角形内の分布についてでは、三角形が位置する象限に応じた符号の分布を使用します。以下に、各象限に対応する記号と描画例を示します。
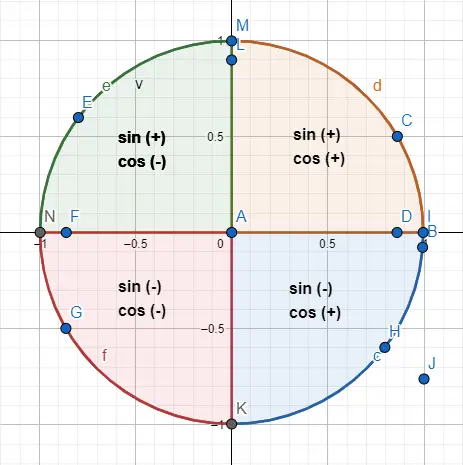
たとえば、角度 30 度と 210 度は同じ数値を共有しますが、それらのサインとコサインは反対の符号を持ちます。つまり、sin(30) = 1/2 および cos(30) = √3/2、一方、sin(210) = -1/2 および cos(210) = -√3/2 となります。この結果を達成するために、円周上の 2 つの角度を表し (下の画像)、標識の指示に従いました。
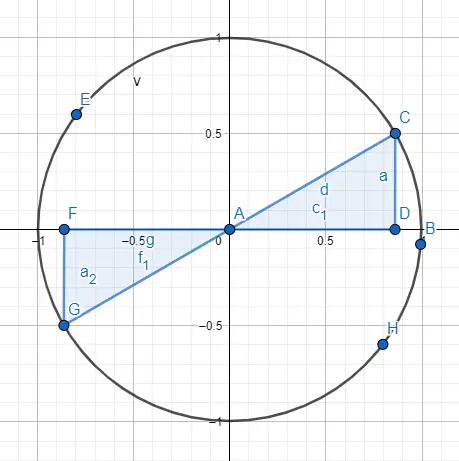
最後に、円周が 360 度しかないため、そうは思えないかもしれませんが、360 度を超える角度をどのようにして設定できるかについて説明します。ただし、750 度の角度を解決したい場合は、0 度から 360 度までの角度に減らすことができます。単純に 750 を 360 で割ると、余りが残りの角度になります。750 度の場合、角度は 30 度になります。
象限に応じた角度の種類
異なる角度の間には関係があるため、比率を計算できます。円に属するすべての角度の三角関数の値。これらの理由を理解しましょう第 1 象限への縮小。これは、特定の角度から第 1 象限までを単純化し、対応する符号を適用することを意味します。以下に、さまざまな手順を説明します (象限に応じて)。
第一象限
この第 1 象限 (0° – 90°) では、与えられた角度で三角比を解くだけで済みます。そして、先ほど記号について説明した両方の図を見ると、サインとコサインの前に正の値が付いています (得られる結果は符号の影響を受けません)。
第 2 象限から第 1 象限への縮小
第 2 象限 (90 度 – 180 度)では補角を扱います。これは、2 つの角度の合計が 180 度になることを意味します。したがって、第 2 象限から第 1 象限への縮小を行う必要があり、式 180 – α = βを使用してそれを行います。ここで、α は第 1 象限の角度、 βは元の角度です。
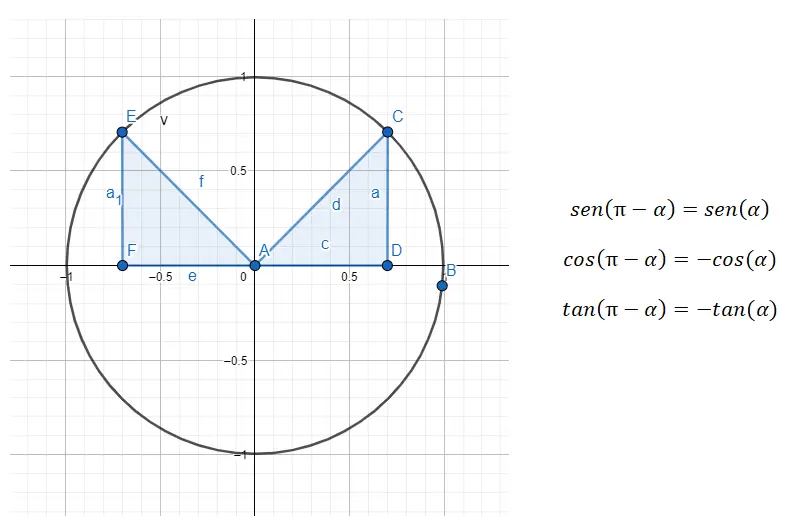
たとえば、角度 135° (第 2 象限に属する) が与えられた場合、最初にこれに関連する第 1 象限からの角度を見つける必要があります。この例では、180 – 45 = 135 であるため、探している角度 (α) は 45 度です。したがって、次のことが当てはまります: sin (135) = sin (180 – 45) = sin (45), cos (135) ) = cos (180 – 45) = -cos (45) および Tan (135) = Tan (180 – 45) = -tan (45)。
第 3 象限を第 1 象限に縮小
第 3 象限 (180 度 – 270 度)では、80 度異なる角度を扱います。これは、角度が 180 度離れていることを意味します。したがって、第 3 象限から第 1 象限に縮小したい場合は、式 180 + α = βを使用する必要があります。ここで、α は第 1 象限の角度、 βは元の角度です。
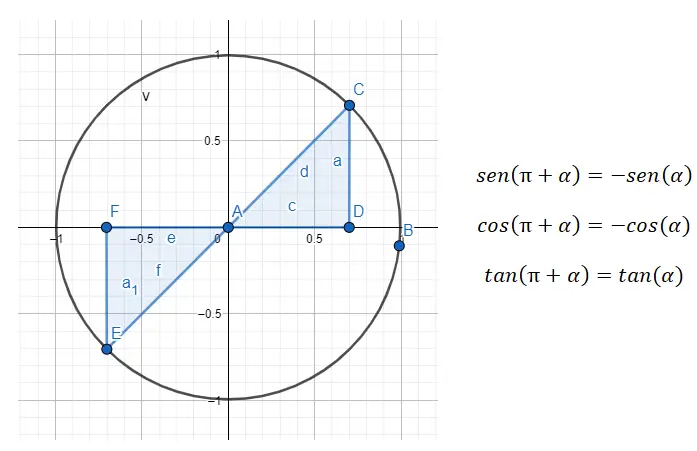
たとえば、角度 225° (第 3 象限に属する) が与えられた場合、それに対応する第 1 象限の角度を見つける必要があります。 225 度の場合、180 + 45 = 225 なので、探している角度 (α) はやはり 45 度です。したがって、sin (225) = sin (180 + 45) = -sin (45), cos (225) =cos(180+45)=-cos(45)、tan(225)=tan(180+45)=tan(45)が成り立ちます。 )。
第 4 象限を第 1 象限に縮小
第 4 象限 (270 度 – 360 度)では、反対の角度を扱います。これは、角度が数値的には等しいが、符号が反対であることを意味します。 、 30° と -30° など (360° – 30° = 330° であるため、330° に相当) 。反対の角度は、正の角度と負の角度、または 2 つの正の角度として記述できることに留意することが重要です (先ほど説明した例で違いを説明しました)。
したがって、第 4 象限から第 1 象限への縮小を行う場合は、式 360 – α = βを使用する必要があります。ここで、α は第 1 象限の角度、 βは元の角度です。
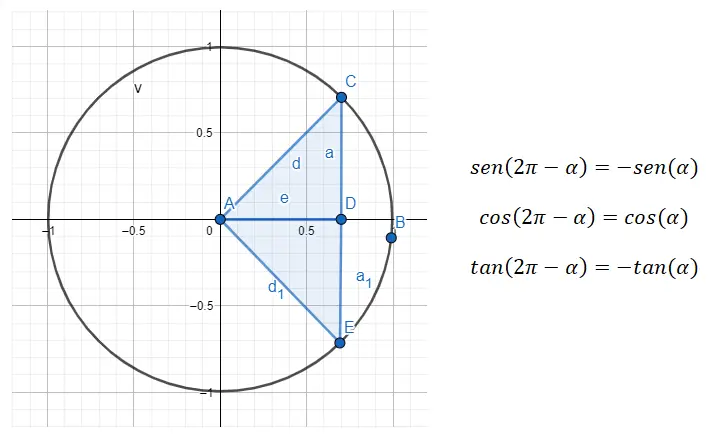
たとえば、角度 315° (第 4 象限に属する) が与えられた場合、最初にこれに関連する第 1 象限の角度を見つける必要があります。探している角度 (α) の場合、360 – 45 = 315 であるため、まだ 45 度です。したがって、sin (315) = sin (360 – 45) = -sin (45), cos ( 315 ) = cos (360 – 45) = cos (45) および Tan (315) = Tan (360 – 45) = -tan (45)。結論として、すべての象限の 45 度から導出される角度がわかりました。
最も重要な角度の三角比
三角法で最も一般的な、注目角 と呼ばれる角度がいくつかあります。自分の三角比を暗記することを強くお勧めします。したがって、以下に、これらの角度の三角比とその導関数 (同じ角度ですが、90、180、または 270 度の差がある) を含む表を作成しました。
| 角度(°) | 角度 (rad) | 胸 | 余弦 | 正接 |
| 0度 | 0ラド | 0 | 1 | 0 |
| 30度 | 1/6πラジアン | 1/2 | √3/2 | √3/3 |
| 45度 | 1/4πrad | √2/2 | √2/2 | 1 |
| 60度 | 1/3πラジアン | √3/2 | 1/2 | √3 |
| 90度 | 1/2πrad | 1 | 0 | ∞ |
| 120度 | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135度 | 3/4πrad | √2/2 | -√2/2 | -1 |
| 150度 | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180度 | πラジアン | 0 | -1 | 0 |
| 225度 | 5/4πrad | -√2/2 | -√2/2 | 1 |
| 270度 | 3/2πrad | -1 | 0 | ∞ |
| 315度 | 7/4πラジアン | -√2/2 | √2/2 | -1 |
三角比の関係
さまざまな三角比を関連付ける方法はいくつかあります。これらの関係から、異なる三角関数間の一種の等式が得られ、これを三角関数恒等式と呼びます。このタイプのアイデンティティのおかげで、他のアイデンティティに基づいて比率を計算できます。三角恒等式にはさまざまなタイプがあり、式自体をサポートする関係のタイプに基づいて分類されることに注意してください。
三角比で解決できる問題
次に、この記事で説明したすべての理論を実践できる一連の演習を提供します。行き詰まったり、質問がある場合は、いつでも記事を読み返すことができます。もう一度読むと、すべてをよりよく理解できることを忘れないでください。つまり、次の練習を始めることができます。
演習 1
角度 225 度の 6 つの三角比を計算します。
まず角度 (α) を計算します。これは 180 + α = 225°、したがって α = 45° となります。
sin(225) = sin(180 + 45) = -sin(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
Tan(225) = Tan(180 + 45) = Tan(45) = 1
演習 2
角度 120 度の 6 つの三角比を計算します。
まず角度 (α) を計算します。これは 180 – α = 120°、したがって α = 60° となります。
sin(120) = sin(180 – 60) = sin(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
Tan(120) = Tan(180 – 60) = -tan(60) = -√3
演習 3
角度 510 度の 6 つの三角比を計算します。
開始する前に、角度を減らす必要があります: 510 / 360 = 1 回転し、残りの角度は 150 です。次に、角度 (α) を計算します。これは 180 – α = 150、したがって α = 30° となります。
sin(150) = sin(180 – 30) = sin(30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
Tan(150) = Tan(180 – 30) = -tan(30) = -√3/3