この記事では、一次関数の導関数がどのくらいになるかを示します。さらに、線形関数の微分の例をいくつか解き、このタイプの微分の公式を示します。一次関数の導関数に関する解決済みの演習も見つかります。
一次関数の導関数は何ですか?
線形関数の導関数は 1 次項の係数です。つまり、線形関数の導関数f(x)=Ax+BはAに等しくなります。
![]()
定数の導関数はゼロであるため、独立項は導関数から削除されます。そして、一方、一次項の導関数は、当該項の係数である。したがって、これら 2 種類の関数の和の微分値が線形項の係数となります。
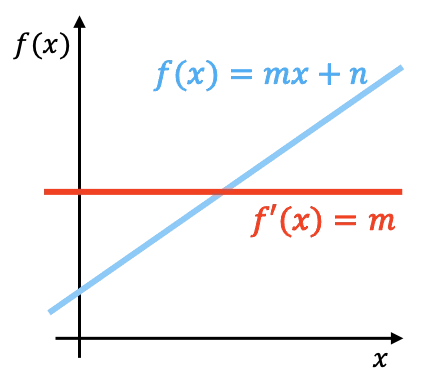
幾何学的には、線形関数の導関数はその関数の傾きです。上のグラフでは、線形関数とその微分関数が表されていることがわかります。
一次関数の導関数の例
線形関数の導関数の定義を考慮して、概念を理解するために線形関数の例をいくつか計算します。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b12cfa0a6432f8171149ec0139d259ce_l3.png)
関数に独立した項がない場合、つまり 1 次の項が 1 つしかない場合、線形関数の導関数は常に変数 x に付随する数値であることに注意してください。例えば:
![]()
したがって、線形関数の導関数は独立変数のない関数、つまり単純な数値になります。
一次関数の導関数の証明
次に、一次関数の導関数の公式を示します。
f を任意の線形関数とします。
![]()
ある点における関数の導関数を計算する式は次のとおりです。
![]()
したがって、線形関数の前の制限を計算すると、次のようになります。
![]()
括弧を解決します。
![]()
分子で演算します。
![]()
最後に、分数を単純化します。
![]()
結論として、一次関数の導関数は、どの点でも 1 次項の係数に等しくなります。したがって、一次関数の導関数の公式が導出されます。
一次関数の導関数の問題を解決しました
次の線形関数の導関数を計算します。
![]()
![]()
![]()
![]()
![]()
![]()
一次関数を導出するには、関数から定数項と変数を単純に削除して、一次項の係数のみを残します。まだ:
![]()
![]()
![]()
![]()
![]()
![]()
関数の係数は分数または根ですが、一次関数の導出も同様に行われます。