逆余弦の微分

ここでは関数の逆余弦を求める方法を説明します。さらに、逆余弦の導関数の例もあり、段階的に解いた演習で練習することができます。最後に、アークコサイン導関数の公式の証明を示します。

逆余弦の導関数は何ですか?

x の逆余弦の導関数は、1 から x の 2 乗を引いた値の平方根を負の 1 で計算したものです。

$f(x)=\text{arccos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{\sqrt{1-x^2}}$

したがって、関数の逆余弦の導関数は、その関数の導関数を 1 からその関数の 2 乗を引いた平方根で割った商を引いたものに等しくなります。

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

実際、最初の式は、2 番目の式の x を u に置き換えることによって得られます。要約すると、逆余弦の導関数の公式は次のとおりです。

ご覧のとおり、 arccosine の導関数の式はarcsine の導関数に似ていますが、その前に負の値が追加されます。

逆余弦導関数の例

逆余弦関数の導関数の公式が与えられたので、このタイプの三角関数導関数のいくつかの例を分析します。こうすることで、関数の逆余弦がどのように導出されるのかを理解しやすくなります。

例 1: 2x の逆余弦の導関数

$f(x)=\text{arccos}(2x)$

逆余弦の導関数を解くには、次の式を使用します。

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

2x の微分値は 2 であるため、2x の逆余弦微分値は、ルート 1 から 2x の 2 乗を引いた値からマイナス 2 になります。

$f(x)=\text{arccos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\sqrt{1-(2x)^2}}=-\cfrac{2}{\sqrt{1-4x^2}}$

例 2: x の 2 乗の逆余弦の導関数

$f(x)=\text{arccos}(x^2)$

逆余弦導関数の公式を連鎖則に適用して導関数を計算します。

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

関数 x ²の導関数は 2x であるため、x の逆余弦の 2 乗の導関数は次のようになります。

$f(x)=\text{arccos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=-\cfrac{2x}{\sqrt{1-x^4}}$

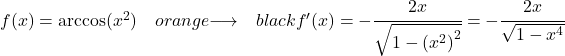
例 3: 対数の逆余弦の導関数

$f(x)=\text{arccos}\bigl(\ln (x)\bigr)$

この例の関数は逆余弦と自然対数から構成される関数なので、連鎖律を使用して導出する必要があります。

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

自然対数の導関数は x で割ったものであるため、整数関数の導関数は次のようになります。

$f(x)=\text{arccos}\bigl(\ln (x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\cfrac{1}{x}}{\sqrt{1-\left(\ln(x)\right)^2}}=\cfrac{1}{x\sqrt{1-\ln^2(x)}}$

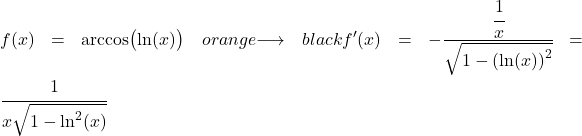
逆余弦導関数で問題が解決されました

次の逆余弦関数を導出します。

$\text{A) }f(x)=\text{arccos}(7x)$

$\text{B) }f(x)=\text{arccos}(x^3+6x)$

$\text{C) }f(x)=\text{arccos}^3\left(e^{3x}\right)$

$\text{D) }f(x)=\text{arccos}\left(\log_3(x^3)\right)$

$\text{E) }f(x)=\text{arccos}\left(\sqrt{4x}\right)$

解決策を参照

$\text{A) }f'(x)=-\cfrac{7}{\sqrt{1-(7x)^2}}=-\cfrac{7}{\sqrt{1-49x^2}}$

$\text{B) }f'(x)=-\cfrac{3x^2+6}{\sqrt{1-(x^3+6x)^2}}$

$\begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}$

$\begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$