根から派生 - マソリティ

ここではルート（根関数）の導関数の取り方を説明します。ルートを分割するための公式と、ルートの導関数を段階的に解決する練習問題が見つかります。

ルートの導関数の公式

根の導関数、または無理関数は、根の指数と同じ根の積で割った基数の導関数 (根号の下の式) を割り、基数の指数から 1 を引いたものに等しくなります。

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

ただし、ルートラジカンドが単なる x の場合、式は簡素化されます。したがって、x の根導関数は次のようになります。

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

つまり、根を求めるには 2 つの公式があります。1 つ目は常に使用でき、2 つ目は基数が x の場合にのみ使用できます。

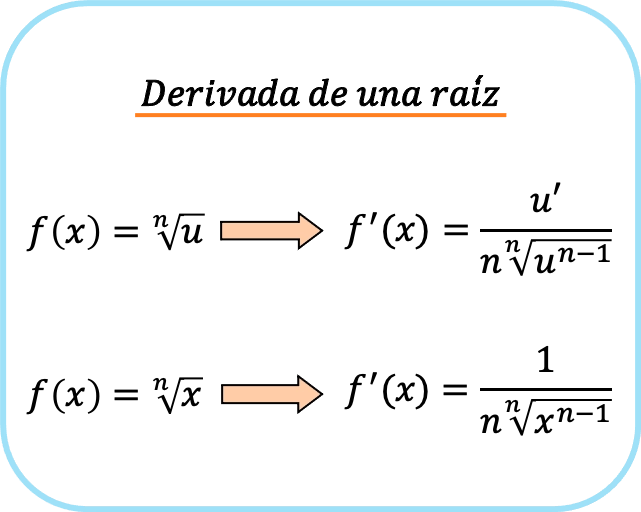
よく見ると、分数の分子の項は、根の導関数を求めるときに連鎖律を適用した結果として得られる項です。これが、基数が x の場合、x の導関数であるため、分母に 1 が表示される理由です。

ルート導関数の例

根関数の導関数の公式を考慮して、根の導関数を求める方法を理解できるように、以下にこのタイプの導関数の例をいくつか説明します。

例 1: 平方根の導関数

次に、平方根の導関数が何であるかを見てみましょう。

$f(x)=\sqrt{x}$

この場合、ルート内の式は単なる x なので、次の式を使用できます。

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

したがって、平方根の導関数は、1 を x の平方根の 2 倍の積で割ったものに等しくなります。

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

例 2: 立方根の導関数

$f(x)=\sqrt[3]{x}$

この例では、ルートの下の式は x であるため、次の式を適用できます。

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

したがって、立方根の導関数は、1 を x の 2 乗の立方根の 3 倍で割ったものに等しくなります。

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

例 3: 4 番目の根の導関数

$f(x)=\sqrt[4]{7x-2}$

現在、根号記号の下に x はありませんが、より複雑な代数式があります。したがって、ルートの導関数には次の一般式を使用する必要があります。

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

根号の下の式は 1 次関数であるため、その導関数は 7 です。したがって、関数全体の導関数は次のようになります。

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

例 4: あるルートから別のルートへの派生

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

別のルートから構成されるこのルートの導関数を解くには、次の公式を適用する必要があります。

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

この場合、導関数を計算するには、同じ式を続けて 2 回使用する必要があります。

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

ルートの導関数の問題を解決しました

次の根の導関数を計算します。

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

解決策を参照

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

ルートの導関数の公式

ルート導関数の例

例 1: 平方根の導関数

例 2: 立方根の導関数

例 3: 4 番目の根の導関数

例 4: あるルートから別のルートへの派生

ルートの導関数の問題を解決しました

コメントする 返信をキャンセル

コメントする返信をキャンセル