ユニタリー行列 - マソリティ

このページでは、ユニタリー行列とは何かを説明し、さらによく理解できるようにいくつかの演習で説明します。また、このタイプの行列の特性が線形代数にとって非常に重要であることもわかります。

ユニタリ行列とは何ですか?

ユニタリ行列の定義は次のとおりです。

ユニタリ行列は、共役転置行列を乗じた複素行列であり、単位行列と等しくなります。つまり、次の条件が満たされます。

$U\cdot U^* = U^* \cdot U =I$

金

$U$

はユニタリ行列であり、

$U^*$

その共役転置。

したがって、この条件は、単位行列の逆行列がその共役転置であることを意味します。なぜなら、逆行列の定義によれば、その積が行列 d’identify と等しい場合、行列は別の行列の逆行列であるからです。。

$\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}$

したがって、ユニタリ行列は常に逆行列を持つため、常に正規行列または非縮退行列になります。

一方、実数環境におけるユニタリ行列の類似物は直交行列であり、この場合、ユニタリ行列に転置を乗算したものが単位行列に等しいことは事実です。

$U\cdot U^t = U^t \cdot U =I$

したがって、この場合、U の逆行列は、直接その転置 (または転置) 行列になります。

単位行列の例

2×2次元の単位行列の例

単位行列の概念を理解したら、それをよく理解するために 2×2 単位行列の例を見てみましょう。

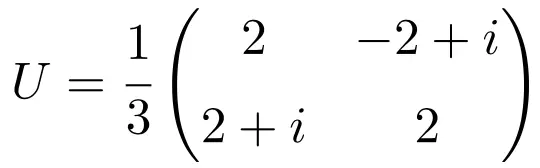
この行列は、それ自体とその共役行列を乗算すると恒等行列 (または単位) 行列が得られるため、ユニタリです。

$\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

そして、前に見たように、ユニタリ行列は共役転置で可換です。

$\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

単位対角行列の例

行列の次元に関係なく、複素数iのみから構成される対角行列もユニタリ行列の一例です。以下は、次元 3 × 3 の単位行列を使用してこれを示す、解決済みの演習です。

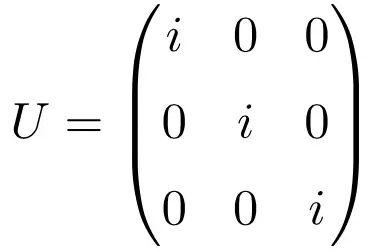
共役転置によって行列の積を解くと、解として恒等行列が得られることに注意してください。

$\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

そして、行列を逆に乗算した場合にも同じことが起こります。

$\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

この行列の特徴は、行列が主対角線上の虚数iによって毎回形成され、残りの要素がゼロ (0) であるため、任意の次元のユニタリ行列の例として機能することです。 ) ユニタリ行列になります。

ユニタリ行列の性質

単位行列のプロパティは次のとおりです。

明らかに、ユニタリ行列は正規行列です。ただし、すべての通常の行列がユニタリ行列であるわけではありません。

ユニタリ行列は常に正方行列です。

すべての単位行列は対角化可能です。つまり、対角行列に変換できます。

単位行列の行列式の絶対値は常に 1 に等しくなります。

$\begin{vmatrix} det(U) \end{vmatrix} = 1$

同一行列はユニタリ行列です。

すべてのために
$n$

、すべての単位行列のセット

$n\times n$

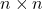
行列積演算により、ユニットグループと呼ばれるグループが形成されます。

したがって、同じ次数の 2 つの単位行列を乗算すると、別の単位行列が得られます。

単位行列のすべての固有値 (または固有値) の係数は常に 1 に等しくなります。

$\begin{vmatrix} \lambda \end{vmatrix} = 1$

このタイプの行列の固有空間は直交しています。

ユニタリ行列とは何ですか?

単位行列の例

2×2次元の単位行列の例

単位対角行列の例

ユニタリ行列の性質

コメントする 返信をキャンセル

コメントする返信をキャンセル