このページは、存在するヘッセ行列の最も完全な説明であることは間違いありません。ここでは、ヘッセ行列の概念とその計算方法を例とともに説明し、実践するための解決された演習もいくつかあります。さらに、多変数関数の最大値と最小値の計算方法や、それが凹関数か凸関数かについても学ぶことができます。最後に、ヘッセ行列のユーティリティとアプリケーションも紹介します。
ヘッセ行列とは何ですか?
ヘッセ行列 (またはヘッセ行列) の定義は次のとおりです。
ヘッセ行列は、 n 変数の関数の偏二次導関数で構成される n × n 次元の正方行列です。
この行列はヘッセ行列としても知られ、一部の数学の本では判別式と呼ばれています。ただし、最も一般的な呼び方はヘッセ行列です。
したがって、ヘッセ行列の式は次のようになります。

したがって、ヘッセ行列は常に関数内の変数の数に等しい次元を持つ正方行列になります。たとえば、関数に 3 つの変数がある場合、ヘッセ行列の次元は 3×3 になります。
さらに、シュワルツの定理(またはクレローの定理) は、微分の順序は重要ではない、つまり、変数に関して部分的に導出することが重要であると述べています。
![]()
次に変数に関して
![]()
に関して偏微分することに相当します
![]()
それなら尊重する
![]()
。
![]()
したがって、ヘッセ行列は対称行列、つまり主対角を軸とする対称性を持ちます。
興味深いことに、ヘッセ行列は、線形代数の分野に非常に重要な貢献をした 19 世紀のドイツの数学者、ルートヴィヒ オットー ヘッセにちなんで名付けられました。
ヘッセ行列の計算例
2 × 2 次元のヘッセ行列を見つける方法の例を見てみましょう。
- 次の関数の点 (1,0) におけるヘッセ行列を計算します。
![]()
まず、一次偏導関数を計算する必要があります。
![]()
![]()
一次導関数がすでにわかったら、すべての二次偏導関数を計算します。
![]()
![]()
![]()
したがって、2 × 2 行列の式からヘッセ行列を見つけることができます。
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-926f350fe0ac3184ec0b563b57fd6041_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b7f3d45918645a5b6019896ed45eda75_l3.png)
したがって、点 (1,0) で評価されるヘッセ行列は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bdccfc61f7befe6c75f66c8a4658f3e6_l3.png)
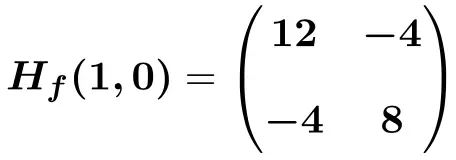
ヘッセ行列の問題を解決しました
演習 1
点 (1,1) で 2 つの変数を使用して、次の関数のヘッセ行列を計算します。
![]()
まず、関数の一次偏導関数を見つける必要があります。
![]()
![]()
一次導関数をすでに計算したら、すべての二次偏導関数を解きます。
![]()
![]()
![]()
したがって、ヘッセ行列は次のように定義されます。
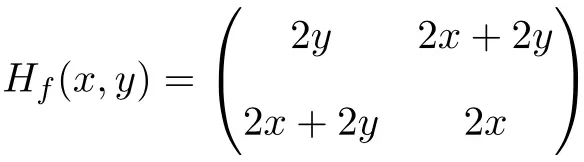
最後に、残っているのは、点 (1,1) でヘッセ行列を評価することだけです。
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5353c0229942269e07455047284f92b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf00fccdb37a19388e76b5a84a408d02_l3.png)
演習 2
2 つの変数で次の関数の点 (1,1) におけるヘッセ行列を計算します。
![]()
まず、関数の一次偏導関数を計算する必要があります。
![]()
![]()
一次導関数を取得したら、関数の二次偏導関数を計算します。
![]()
![]()
![]()
したがって、関数のヘッセ行列は 2×2 次元の正方行列になります。
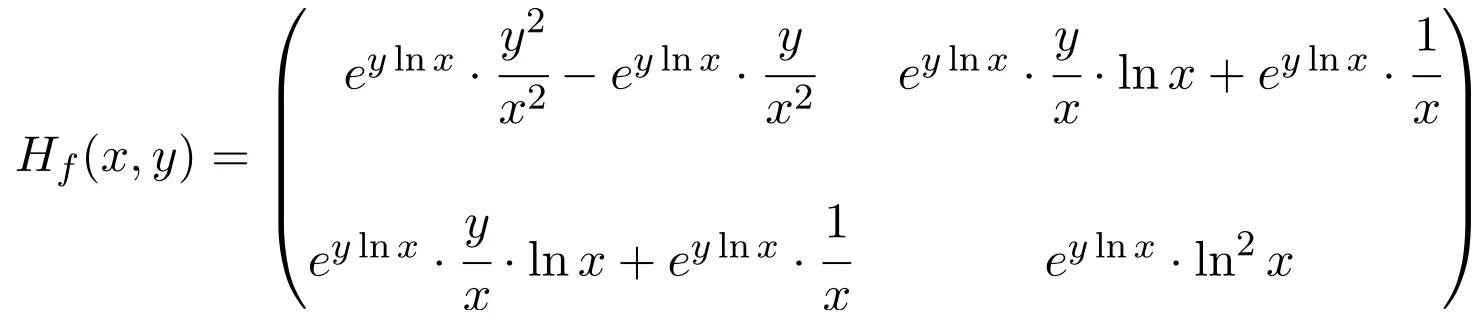
最後に、残っているのは、点 (1,1) でヘッセ行列を評価することだけです。
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c316cc61e6d007e5d034274e0f494520_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e456b856c722a140d73ade63f13ec9f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-929fbf6e7f0f90110d11d4ccd51fd51a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce780ddb8c09515afccfb2da2d842584_l3.png)
演習 3
点でのヘッセ行列を求めます
![]()
3 つの変数を使用した次の関数:
![]()
まず、関数の一次偏導関数を計算します。
![]()
![]()
![]()
一次導関数を取得したら、関数の二次偏導関数を計算します。
![]()
![]()
![]()
![]()
![]()
![]()
したがって、関数のヘッセ行列は 3 × 3 次元の正方行列になります。
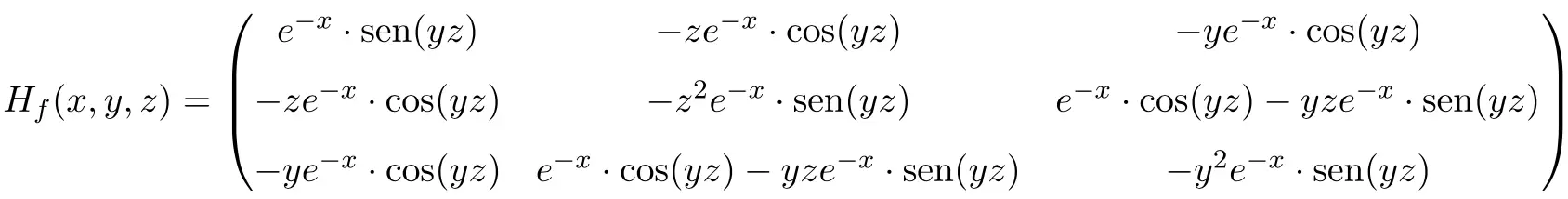
最後に、変数をその時点のそれぞれの値に置き換えます
![]()
![Rendered by QuickLaTeX.com \displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e198192f67babd81228caa53b66e8a0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ce9c6b4cfcddfb0c2eb51db1189c653_l3.png)
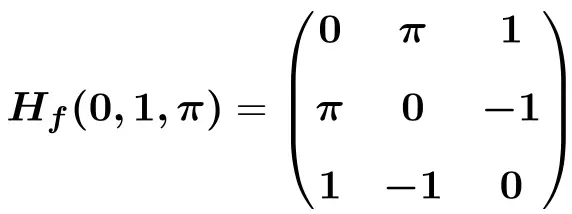
演習 4
4 つの変数を使用して、次の関数の点 (2,-1,1,-1) におけるヘッセ行列を決定します。
![]()
最初のステップは、関数の一次偏導関数を見つけることです。
![]()
![]()
![]()
![]()
次に、関数の 2 次偏導関数を解きます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
したがって、すべての偏導関数を解くことによって得られる 4×4 ヘッセ行列の式は次のようになります。
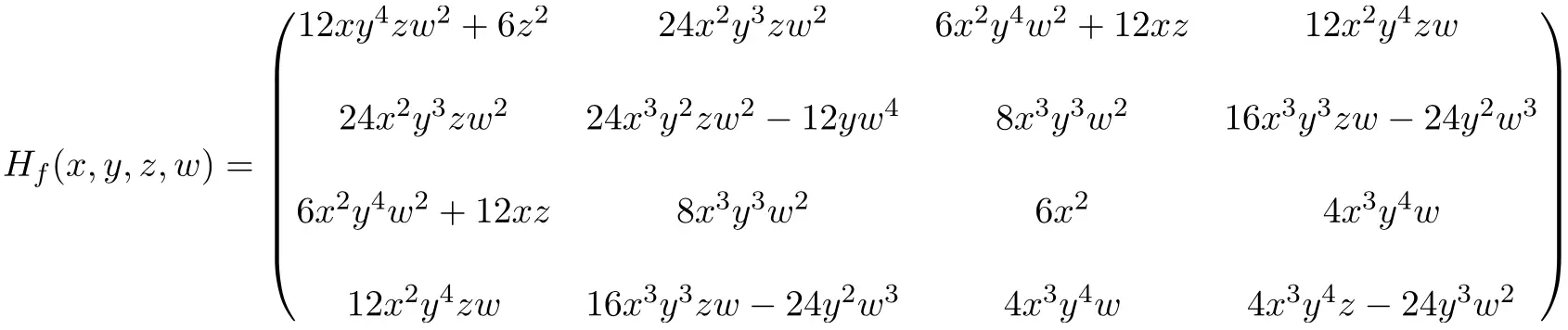
最後に、未知数をそれぞれの点の値 (2,-1,1,-1) に置き換えて計算を行います。
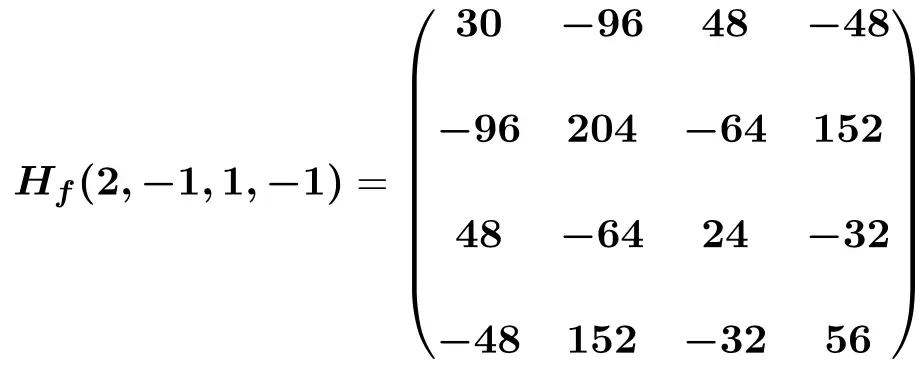
ヘッセ行列が正、負、または不定であることはどのようにしてわかりますか?
後で説明するように、ヘッセ行列が正の半定値、正の定値、負の半定値、負の定値、または不定の行列であるかどうかを知ることは非常に役立ちます。それでは、どのように調べられるかを見てみましょう。
固有値(または固有値)の基準
行列のタイプを知る 1 つの方法は、ヘッセ行列の固有値 (または固有値) を調べることです。
- ヘッセ行列は、ゼロ以上の固有値 (または固有値) を持つ場合、正の半定値です。つまり、正の固有値と 0 に等しい固有値が少なくとも 1 つあります。
![]()
- ヘッセ行列は、そのすべての固有値 (または固有値) がもっぱら 0 (正) より大きい場合、正定行列です。
 半定値です。つまり、負の固有値と 0 に等しい固有値が少なくとも 1 つあります。
半定値です。つまり、負の固有値と 0 に等しい固有値が少なくとも 1 つあります。
![]()
- ヘッセ行列は、すべての固有値 (または固有値) が 0 (負) 未満の場合、負定行列です。
![]()
- ヘッセ行列は、正と負の固有値 (または固有値) を持つ場合、定義されません。
![]()
シルベスター基準
ヘッセ行列がどのタイプであるかを知るもう 1 つの方法は、シルベスターの基準を使用することです。ただし、この定理では、行列が正定値、負定値、または不定値であるかどうかのみがわかります。ただし、一般に計算が簡単なため、使用した方がはるかに高速になる場合もあります。
したがって、シルベスター基準は次のようになります。
- ヘッセ行列のすべての主副行列が 0 より大きい場合、その行列は正定行列です。
- 偶数のインデックスを持つヘッセ行列の主マイナーが 0 より大きく、奇数のインデックスを持つ主マイナーが 0 未満の場合、それは負定行列です。
- ヘッセ行列のすべての主副行列が 0 以外で、前の 2 つの条件のどちらも満たされない場合、その行列は不定行列になります。
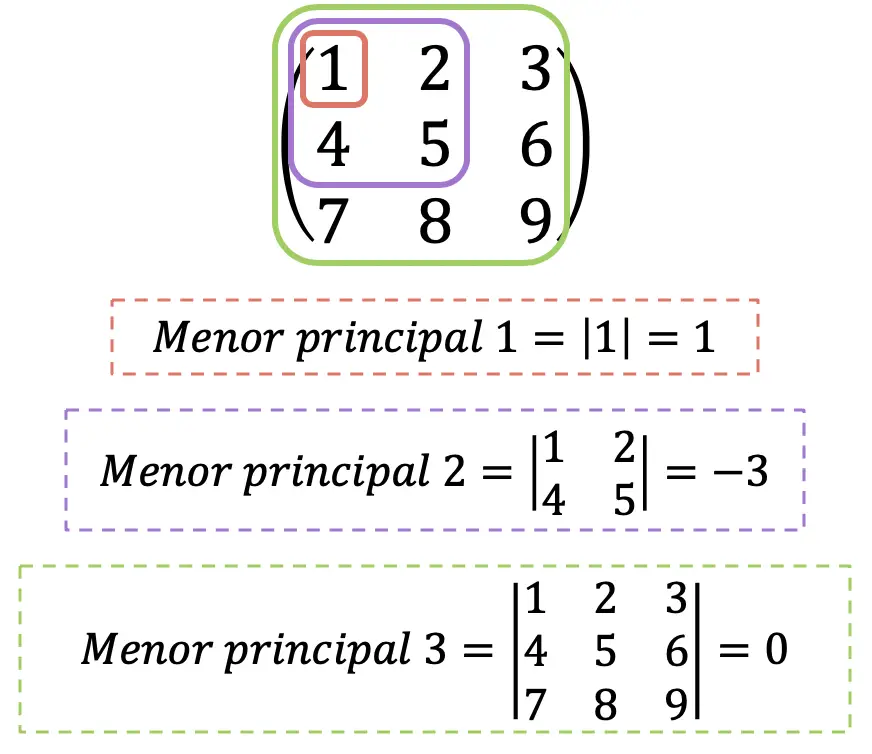
明らかに、ヘッセ行列の最大主短関数は常に行列式と一致します。情報提供のみを目的として、ヘッセ行列の行列式は「ヘッセ行列」とも呼ばれますが、ここでは混乱を避けるためにそうしません。
ヘッセ行列を使用して関数の最大値または最小値を計算する方法
ヘッセ行列の計算方法を理解すると、おそらくこの行列は何に使用されるのか疑問に思うでしょう。
ヘッセ行列の応用の 1 つは、複数の変数を持つ関数の最大値または最小値を見つけることです。ここでは、最大値と最小値を計算する方法を段階的に説明します。
- まず、多変数関数の臨界点が計算されます。これを行うには、関数の勾配またはヤコビ行列を計算し、それを 0 に設定して方程式を解きます。
- ヘッセ行列が計算されます。
- ステップ 1 で見つかった臨界点がヘッセ行列に代入されます。したがって、関数を持つ臨界点と同じ数のヘッセ行列を取得します。
- 各ヘッセ行列がどのようなタイプの行列であるかを見ていきます。つまり、正定値、負定値、不定値などであるかどうかを確認します。
- ヘッセ行列が正定値の場合、臨界点は関数の相対最小値になります。
- ヘッセ行列が負定値の場合、臨界点は関数の相対最大値になります。
- ヘッセ行列が定義されていない場合、臨界点は鞍点になります。
多変数関数の最大値と最小値を計算する例
これがどのように行われるかを確認するために、ヘッセ行列を使用して関数の相対極値を計算および分類する例を次に示します。
- 次の多変数関数の相対極値をすべて求めます。
![]()
最初に行う必要があるのは、関数のヤコビ行列を計算することです。この場合、これはスカラー関数であるため、勾配と一致します。
![]()
ここで臨界点を決定する必要があります。これを行うために、得られた方程式を 0 に等化し、連立方程式を解きます。
![]()
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d851eb626a9bd385aec8f68c9df71a39_l3.png)
したがって、私たちが見つけた臨界点は (0,-2) です。
関数の臨界点が見つかったら、ヘッセ行列を計算する必要があります。
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-702fa5f5c3e3d872e1ec0dad0e3216c7_l3.png)
そして明らかに、臨界点で評価されるヘッセ行列は同じです。
![Rendered by QuickLaTeX.com \displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b56ffff28d1a9b98c9848891ae924eb_l3.png)
それがどのタイプの行列であるかを確認するために、シルベスター基準を使用します。したがって、行列の主なマイナーを解きます。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8](https://mathority.org/wp-content/ql-cache/quicklatex.com-d66efe9fca481475009bb1703939e4f6_l3.png)
主短調 1 (奇数) は正、主短調 2 (偶数) は負であるため、シルベスターの基準によれば、これは不定行列になります。したがって、臨界点 (0,-2) は鞍点です。
ヘッセ行列を使用した関数の凹性または凸性の決定
ヘッセ行列のもう 1 つの用途は、関数が凹か凸かを知ることです。そして、これは次の定理に従って決定できます。
なれ
![]()
オープンセットと
![]()
二次導関数が連続である関数。その凹面と凸面はヘッセ行列によって定義されます。
- 関数

全体的に凸状になっている

そのヘッセ行列がセットのすべての点で正の半定値である場合に限ります。
- 関数

全体的に厳密に凸状である

そのヘッセ行列がセットのすべての点で正定値である場合に限ります。
✓したがって、もし
![]()
はヤコビ行列も消滅する点における凸関数であり、この点は局所最小値です。
- 関数

全体的に凹んでいる

そのヘッセ行列がセットのすべての点で負の半定値である場合に限ります。
- 関数

全体的に厳密に凹んでいます

そのヘッセ行列がセットのすべての点で負定値である場合に限ります。
✓したがって、もし
![]()
はヤコビ行列も消滅する点で凹型の関数であり、この点は極大値です。
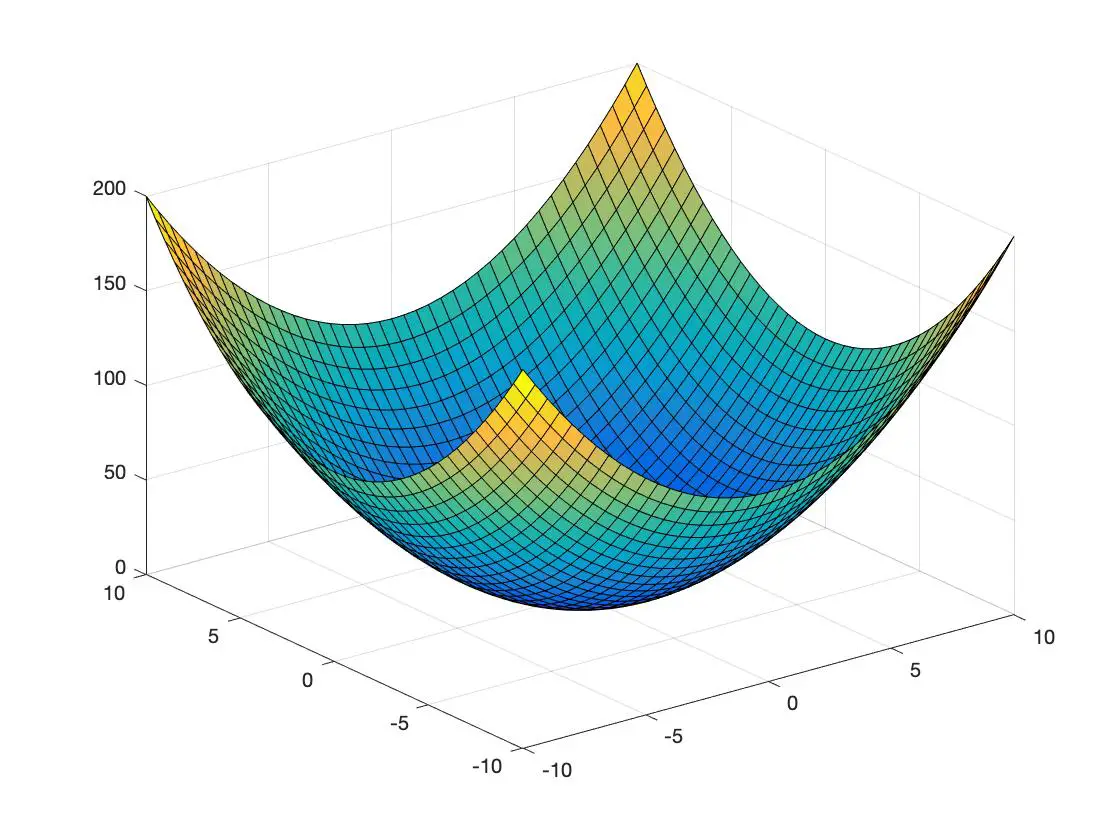
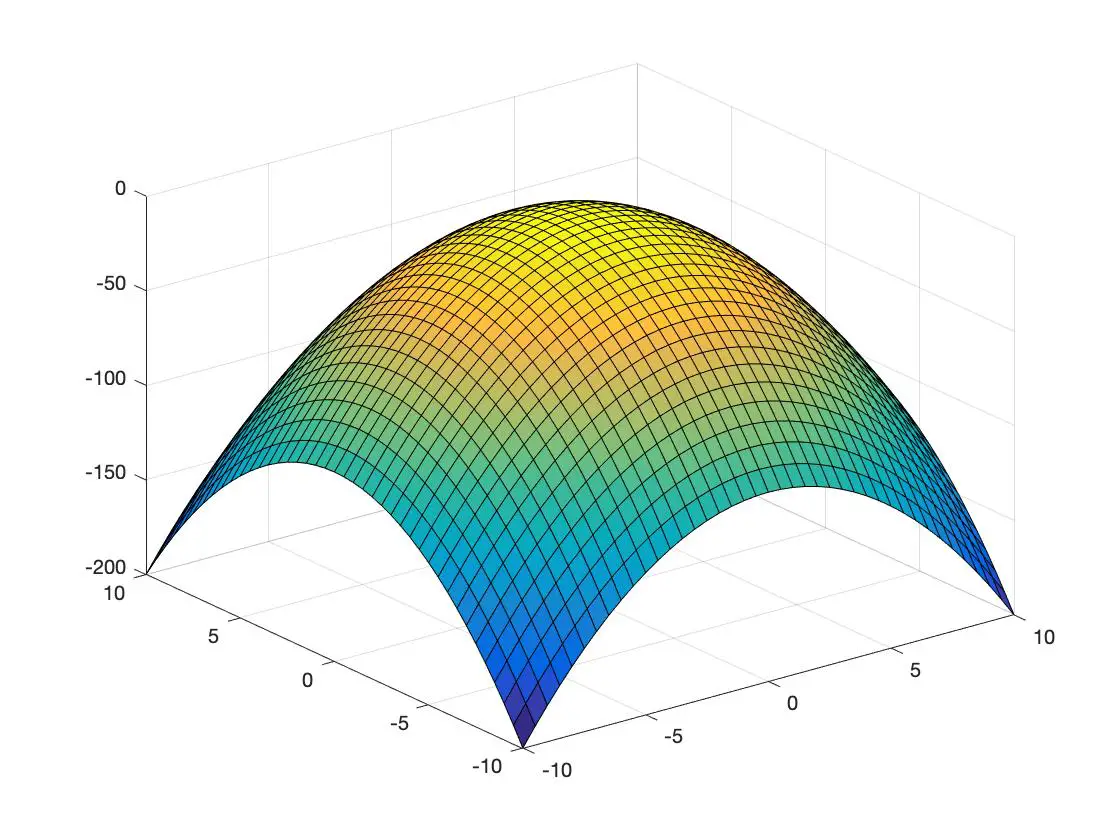
以下に、3 次元空間で表現された凸関数と凹関数の例を示します。
凸関数
凹関数
ヘッセ行列のその他の応用
ヘッセ行列の主な用途はすでに見たものですが、他の用途もあります。最も興味のある方のために、以下で説明します。
テイラー多項式
点における 2 つ以上の変数の関数に対するテイラー多項式の展開
![]()
次のように始まります:
![]()
ご覧のとおり、テイラー展開の 2 次項は、多項式の展開点で評価されたヘッセ行列によって与えられます。
ボーダー付き黄麻布マトリックス
ヘッセ行列のもう 1 つの用途は、多変量関数の最小値と最大値を計算することです。
![]()
別の役割に制限される
![]()
。この問題を解決するには、有界ヘッセ行列を使用し、次の手順に従います。
ステップ 1:ラグランジュ関数が計算されます。これは次の式で定義されます。
![]()
ステップ 2:ラグランジュ関数の臨界点を見つけます。これを行うには、ラグランジュ関数の勾配を計算し、方程式を 0 に設定して方程式を解きます。
![]()
![]()
ステップ 3:見つかった各点について、次の行列で定義される有界ヘッセ行列を計算します。
![Rendered by QuickLaTeX.com \displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3d1b2b04de9559a521e6704151c27bc4_l3.png)
ステップ 4:各臨界点について、それが最大値であるか最小値であるかを判断します。
- これは関数の極大値になります

関数制約の下で
臨界点で評価された境界付きヘッセ行列の最後のnm ( nは変数の数、 m は制約の数) の主マイナーの場合、負の符号で始まる交互の符号が付きます。
- これは関数の極小値になります

関数制約の下で
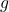
最後のnm ( nは変数の数、 m は制約の数) の場合、臨界点で評価されたシャープ ヘッセ行列の主マイナーはすべて負の符号を持ちます。
ある制約付き関数の別の関数に対する相対的な最小値または最大値は、制限されていない関数についても必ずしもそうである必要はないことに留意する必要があります。したがって、境界付きヘッセ行列は、このタイプの問題にのみ役立ちます。
他の業務との関係
最後に、ヘッセ行列は、主にヤコビ行列やラプラス演算子など、他の重要な演算や行列にもリンクされています。
ヤコビアン行列との関係
関数のヘッセ行列
![]()
は、同じ関数の勾配のヤコビ行列です。
![]()
ラプラス演算子
ヘッセ行列トレースは、ラプラス演算子と同等です。
![]()
ラプラス演算子の定義は関数の勾配の発散であるため、この等価性は簡単に証明できます。
![]()
したがって、その式は次のようになります。
![]()
そして、この合計はヘッセ行列の痕跡にすぎないため、等価性が証明されます。