このページでは、パラメーターを使用して連立方程式を議論し解く方法を説明します。さらに、連立一次方程式の例と解答済みの練習問題も見つかります。
一方、連立一次方程式を解析するには、クラマー則とは何か、 ルーシェ・フロベニウスの定理とは何かを理解しておくことが重要です。これらは常に使用することになるためです。
パラメータを使用した連立一次方程式の例
- パラメーターmに関して次の連立方程式を議論して解きます。
![Rendered by QuickLaTeX.com \begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ab2286d15c20029b98a5ea4622033d4_l3.png)
まず、システムの行列 A と拡張行列 A’ を作成します。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef8e6b26595703c77c65178cbf90ffc_l3.png)
次に、Sarrus の法則を使用して A の行列式を解き、行列がどのランクであるかを確認します。
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e823f83f25f798bd854612a7352680d4_l3.png)
したがって、 A の行列式の結果はmの値に依存します。したがって、 mのどの値について行列式が消えるかを見てみましょう。これを行うには、結果を 0 に設定します。
![]()
そして、二次方程式を次の式で解きます。
![]()
![Rendered by QuickLaTeX.com \displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e863082ac1f9b43df4de9fe93f5eb305_l3.png)
したがって、 mが 2 または 3 に等しい場合、A の行列式は 0 になります。また、 m が2 または 3 とは異なる場合、A の行列式は 0 とは異なります。
したがって、各ケースを個別に分析する必要があります。
m≠3 および m≠2:
先ほど見たように、パラメーターmが 2 および 3 と異なる場合、行列 A の行列式は 0 とは異なります。したがって、 A のランクは 3 です。
![]()
さらに、行列 A’ の階数も 3 です。これは、その中に行列式が 0 とは異なる 3×3 部分行列があるためです。また、「4×4 行列式を作ることはできない」ため、階数 4 にすることはできません。
![]()
次に、行列 A のランクは行列 A’ のランクとシステムの未知数の数 (3) に等しいため、ルーシェ-フロベニウスの定理により、それが決定されたシステム互換性(SCD) であることがわかります。 :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
システムが互換性決定システム (DCS) であることがわかったら、それを解決するためにCramer の法則を適用します。これを行うには、行列 A、その行列式、および行列 A’ が次のとおりであることを思い出してください。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef8e6b26595703c77c65178cbf90ffc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac47361358555f733a42cffecabdbe9_l3.png)
クラマー則で x を計算するには、行列 A の行列式の最初の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b17f49436fdadbb014011b5c461a4a56_l3.png)
Cramer の規則を使用して y を計算するには、A の行列式の 2 番目の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a2bf75bdabfb2c83870f1869ce19e3d_l3.png)
Cramer の規則を使用して z を計算するには、A の行列式の 3 番目の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eebb3c4d280afc8a9aed8877ddcd4ac5_l3.png)
したがって、m≠3 および m≠2 の場合の連立方程式の解は次のようになります。
![]()
ご覧のとおり、この場合、連立方程式の解は m の関数です。
m が 2 および 3 と異なる場合の解を見つけたら、m が 2 に等しい場合の系を解きます。
m=2:
ここで、パラメーターm が2 に等しい場合のシステムを分析します。この場合、行列 A と A’ は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f42ec4801f3e84cd44b4e0b2ae6351cf_l3.png)
前に見たように、m=2 の場合、A の行列式は 0 です。したがって、行列 A はランク 3 ではありません。しかし、その内部には 0 とは異なる 2×2 行列式があります。たとえば、次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-55ef6cd148fca7a869e14760007e1f2e_l3.png)
したがって、この場合、A のランクは 2 です。
![]()
行列 A のランクがわかったら、A’ のランクを計算します。最初の 3 列の行列式は 0 を与えるため、行列 A’ 内の他の可能な 3×3 行列式を試します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c68c742cae37c52ad2566b7feec5301_l3.png)
次元 3×3 の考えられるすべての行列式は 0 になります。しかし、明らかに、行列 A’ は行列 A と同じ 2×2 の非 0 行列式を持ちます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-55ef6cd148fca7a869e14760007e1f2e_l3.png)
したがって、行列 A’ もランク 2 になります。
![]()
したがって、行列 A のランクは行列 A’ のランクに等しいが、これら 2 つはシステム (3) の未知数の数より小さいため、ルーシェ-フロベニウスの定理によって、これは不定互換性のあるシステムであることがわかります。 (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
これは ICS であるため、これを解決するにはシステムを変換する必要があります。これを行うには、まずシステムから方程式を削除する必要があります。この場合、最後の方程式を削除します。
![Rendered by QuickLaTeX.com \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10c7facda35cb8894e6bbb236e4953f1_l3.png)
次に、変数 z を λ に変換しましょう。
![Rendered by QuickLaTeX.com \begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0155083595420da31a486927e953805c_l3.png)
そして、λ を含む項を独立した項に置きます。
![Rendered by QuickLaTeX.com \begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8486baee4be39f417988ee12b5e67c7_l3.png)
したがって、システムの行列 A と行列 A’ は残ります。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8591e8c21bce2f49998311bbb08f7dee_l3.png)
最後に、システムを変換したら、 Cramer のルールを適用します。これを行うには、まず A の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3](https://mathority.org/wp-content/ql-cache/quicklatex.com-c34669d7234c9736c350f793df337bd3_l3.png)
Cramer の規則を使用してxを計算するには、A の行列式の最初の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-987ebe052154332042afeb27535996f1_l3.png)
Cramer の規則を使用してyを計算するには、A の行列式の 2 番目の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a3c7b2cd7319f7f9db6df7df79abb50_l3.png)
したがって、m=2 の場合、連立方程式の解は λ の関数になります。これは SCI であるため、無限の解が存在します。
![]()
パラメーターm が2 および 3 と異なる場合、および 2 に等しい場合のシステムの解をすでに分析しました。 したがって、必要なのは最後のケース、つまりm が3 の値を取る場合だけです。
m=3:
ここで、パラメーターm が3 の場合に何が起こるかを分析します。この場合、行列 A と A’ は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49bbc0d7d36606aa59be050c2682de5_l3.png)
前に見たように、m=3 の場合、A の行列式は 0 です。したがって、行列 A はランク 3 ではありません。しかし、その内部には 0 とは異なる 2×2 の行列式があります。たとえば、次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d88ce42feb4bba9aa74aae98e1062c4a_l3.png)
したがって、この場合、A のランクは 2 です。
![]()
行列 A のランクがわかったら、A’ のランクを計算します。最初の 3 列の行列式は 0 を与えるため、行列 A’ 内にある別の 3×3 行列式、たとえば最後の 3 列の行列式を試します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e6f1a5c155ca004c73e51bdcbe5ece9_l3.png)
一方、行列 A’ には結果が 0 とは異なる行列式が含まれているため、行列 A’ のランクは 3 になります。
![]()
したがって、m = 3 の場合、行列 A のランクは行列 A’ のランクよりも低くなります。したがって、ルーシェ-フロベニウスの定理から、システムは互換性のないシステム(IS) であると推定されます。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3454f804b63f3cca9bcf08bc93815f90_l3.png)
したがって、 m = 3 の場合、連立方程式には解がありません。
例の要約:
これまで見てきたように、連立方程式の解はパラメーターmの値に依存します。考えられるすべてのケースの概要は次のとおりです。
- m≠3 および m≠2:
![Rendered by QuickLaTeX.com \displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf366a55bd307517f94fd8aa00cdf598_l3.png)
- m=2:
![Rendered by QuickLaTeX.com \displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94002d4f4d866569ed7d6993dd977b81_l3.png)
- m=3:
![]()
システムには解決策がありません。
ここでは、ルーシュの定理とクラマーの法則を使用してプロセス全体を実行しましたが、パラメーターを含む連立方程式は、ガウスの方法 (演習付き)によって議論および解決することもできます。この方法の詳細については、リンク先のページで学ぶことができます。このページには、手順の詳細な説明、例、および解決された演習が段階的に記載されています。
パラメータ付き一次方程式系のディスカッション問題を解決しました
演習 1
次のパラメータ依存線形方程式系について議論して解きます。
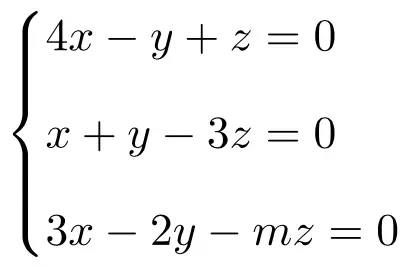
まず、システムの行列 A と拡張行列 A’ を作成します。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b641845325965882d4aac899246cffb3_l3.png)
次に、行列 A のランクを見つける必要があります。これを行うには、行列全体の行列式が 0 と異なるかどうかを確認します。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d36c7cffe0248a2f45cd5871abc6ed5_l3.png)
A の行列式の結果は、m の値に依存します。したがって、m のどの値について行列式が消えるかを見てみましょう。これを行うには、結果の結果を 0 に等しくして、方程式を解きます。
![]()
![]()
![]()
したがって、m が -4 の場合、A の行列式は 0 になります。また、m が -4 と異なる場合、A の行列式は 0 とは異なります。したがって、各ケースを個別に分析する必要があります。
m≠-4:
先ほど見たように、パラメーター m が -4 と異なる場合、行列 A の行列式は 0 とは異なります。したがって、A のランクは 3 になります。
![]()
さらに、行列 A’ の階数も 3 です。その中には行列式が 0 とは異なる 3×3 部分行列があるためです。また、「4×4 行列式を作ることはできない」ため、階数 4 になることはあり得ません。
![]()
したがって、ルーシェ-フロベニウスの定理を適用すると、 A の範囲が A’ の範囲および未知数の数に等しいため、これが互換性のある決定系(SCD) であることがわかります。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
システムが SCD であることがわかったら、それを解決するために Cramer の法則を適用します。これを行うには、行列 A、その行列式、および行列 A’ が次のとおりであることを思い出してください。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9e0bd352ad7713a03824ead1239041c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20](https://mathority.org/wp-content/ql-cache/quicklatex.com-530cb4576ee1a91d6246ed6cf9dd0fc8_l3.png)
Cramer の規則を使用して xatex] を計算するには、A の行列式の最初の列を独立項の列で変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b076bbda8d086abedb459570d74c80a9_l3.png)
未知数を計算するには、クラマーの法則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f642a8cb2fd174e5c383a4df53e11a2e_l3.png)
Cramer の規則を使用して z を計算するには、A の行列式の 3 番目の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5020a9ba4995b9715d8d1fb4720952b1_l3.png)
したがって、m≠-4 の場合の連立方程式の解は次のようになります。
x=0 y=0 z=0
m=-4:
次に、パラメーター m が -4 の場合のシステムを分析します。この場合、行列 A と A’ は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e585e6465d27ea27ccc2c1a6ec1fe9ae_l3.png)
前に見たように、m=-4 の場合、A の行列式は 0 です。したがって、行列 A はランク 3 ではありません。しかし、その内部には 0 とは異なる 2×2 の行列式があります。たとえば、次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62d150aef4ec798814d25c988b0afd7_l3.png)
行列には 0 とは異なる次数 2 の行列式があるため、行列 A はランク 2 になります。
![]()
A のランクがわかったら、A’ のランクを計算します。最初の 3 列の行列式が 0 を与えることはすでにわかっているので、他の可能な 3×3 行列式を試します。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-39fc49c7a63920c8956703a4851ecfc0_l3.png)
行列 A’ の 3×3 行列式はすべて 0 であるため、行列 A’ もランク 3 にはなりません。ただし、内部には 0 とは異なる次数 2 の行列式が含まれています。例:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62d150aef4ec798814d25c988b0afd7_l3.png)
したがって、行列 A’ はランク 2 になります。
![]()
行列 A の範囲は行列 A’ の範囲に等しいですが、これら 2 つは系 (3) の未知数の数より小さいため、ルーシェ-フロベニウスの定理によれば、c は不定互換系 (ICS) です。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f43fdf4978386c61d18f9bb5b5883881_l3.png)
これは ICS システムなので、それを解決するにはシステムを変換する必要があります。まず、1 つの方程式を削除します。この場合、それが最後の方程式になります。
![Rendered by QuickLaTeX.com \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d5499fda37d3cbf56fbf6ecbfc6bfba_l3.png)
次に、変数 z を λ に変換しましょう。
![Rendered by QuickLaTeX.com \begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96ea68274b072531365282e01d926718_l3.png)
そして、λ を含む項を独立した項に置きます。
![Rendered by QuickLaTeX.com \begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6192715e62cc8e3d3fe4c51da8629c70_l3.png)
システムの行列 A と行列 A’ はそのまま残ります。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-99a91208ff1742f81e799aa5ab7f9097_l3.png)
最後に、システムを変換したら、クラマーの法則を適用します。これを行うには、まず A の行列式を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5](https://mathority.org/wp-content/ql-cache/quicklatex.com-34832b783ddaf4af205302240d0feafb_l3.png)
Cramer の規則を使用して x を計算するには、A の行列式の最初の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-362167d2eaa02d7243dedd5c385d08b1_l3.png)
未知数を計算するには、クラマーの法則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ede5a3a87ac0bb9ceea4232ec7b381fd_l3.png)
したがって、m=-4 の場合、連立方程式の解は λ の関数になります。これは SCI であるため、無限の解が存在します。
![]()
演習 2
次のパラメータ依存一次方程式系について議論し、解を見つけてください。
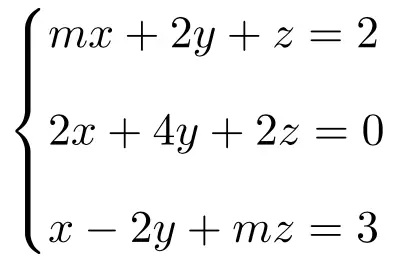
最初に行うことは、システムの行列 A と拡張行列 A’ です。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e924dd1b3fe5c0da561b92da9bf5da3b_l3.png)
次に、行列 A のランクを見つける必要があります。これを行うには、行列全体の行列式が 0 と異なるかどうかを確認します。
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d0f8dbb7408ac6521e0144ac2f3a8a3_l3.png)
A の行列式の結果は、m の値に依存します。したがって、m のどの値について行列式が消えるかを見てみましょう。これを行うには、結果の結果を 0 に等しくして、方程式を解きます。
![]()
![]()
![]()
![]()
![]()
したがって、m が +1 または -1 の場合、A の行列式は 0 になります。また、m が +1 および -1 と異なる場合、A の行列式は 0 とは異なります。したがって、各ケースを次のように分析する必要があります。
m≠+1 および m≠-1:
先ほど見たように、パラメーター m が +1 および -1 と異なる場合、行列 A の行列式は 0 とは異なります。したがって、A のランクは 3 になります。
![]()
さらに、行列 A’ の階数も 3 です。その中には行列式が 0 とは異なる 3×3 部分行列があるためです。また、「4×4 行列式を作ることはできない」ため、階数 4 になることはあり得ません。
![]()
したがって、ルーシェ-フロベニウスの定理を適用すると、 A の範囲が A’ の範囲および未知数の数に等しいため、これが互換性のある決定系(SCD) であることがわかります。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
システムが SCD であることがわかったら、それを解決するために Cramer の法則を適用します。これを行うには、行列 A、その行列式、および行列 A’ が次のとおりであることを思い出してください。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e924dd1b3fe5c0da561b92da9bf5da3b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5114be5e37d2c91f02f22fba22edc42_l3.png)
Cramer の規則を使用して x を計算するには、A の行列式の最初の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b7402e02ee62bd78a6f880d3d122119_l3.png)
未知数を計算するには、クラマーの法則を使用して、A の行列式の 2 番目の列を独立項の列で変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-551c66a9530d0195a9a4ff64d42350c4_l3.png)
Cramer の規則を使用して z を計算するには、A の行列式の 3 番目の列を独立項の列に変更し、それを A の行列式で割ります。
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-28375ce522b7644a745a9adea4c78ae7_l3.png)
したがって、m≠+1 および m≠-1 の場合の連立方程式の解は次のようになります。
![]()
m=+1:
ここで、パラメーター m が 1 に等しい場合のシステムを分析します。この場合、行列 A と A’ は次のとおりです。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6af272a99ed7c281ee8dd9199698686_l3.png)
前に見たように、m=+1 の場合、A の行列式は 0 です。したがって、行列 A はランク 3 ではありません。しかし、その内部には 0 とは異なる 2×2 行列式があります。たとえば、次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ebedf6c9e4316844dc99ceca9472fac5_l3.png)
行列には 0 とは異なる次数 2 の行列式があるため、行列 A はランク 2 になります。
![]()
A のランクがわかったら、A’ のランクを計算します。最初の 3 列の行列式が 0 になることはすでにわかっているので、たとえば最後の 3 列の行列式を試してみます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d0109b155be9f87a0cee337ddec5517_l3.png)
一方、行列 A’ には、結果が 0 とは異なる 3×3 行列式が含まれているため、行列 A’ のランクは 3 になります。
![]()
したがって、m=+1 の場合、行列 A のランクは行列 A’ のランクよりも小さくなります。したがって、ルーシェ-フロベニウスの定理から、システムは互換性のないシステム (IS) であると推定されます。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bb3fec88cf5c6d788afb4480ab1f58_l3.png)
したがって、 m=+1 の場合、連立方程式は互換性のない系であるため、解がありません。
m=-1:
次に、パラメーター m が -1 の場合のシステムを分析します。この場合、行列 A と A’ は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-46b0a00ef38d0e5a433b418de7eb1ec3_l3.png)
前に見たように、m=-1 の場合、A の行列式は 0 です。したがって、行列 A はランク 3 ではありません。しかし、その内部には 0 とは異なる 2×2 の行列式があります。たとえば、次のようになります。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff5373c7e7901f253421efbbd52d192e_l3.png)
行列には 0 とは異なる次数 2 の行列式があるため、行列 A はランク 2 になります。
![]()
A のランクがわかったら、A’ のランクを計算します。最初の 3 列の行列式が 0 になることはすでにわかっているので、たとえば列 1、3、および 4 の行列式を試してみます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20](https://mathority.org/wp-content/ql-cache/quicklatex.com-a95e30910bd64db920f3c2bcb5f2ff62_l3.png)
一方、行列 A’ には、結果が 0 とは異なる 3×3 行列式が含まれているため、行列 A’ のランクは 3 になります。
![]()
したがって、m = -1 の場合、行列 A のランクは行列 A’ のランクよりも低くなります。したがって、ルーシェ-フロベニウスの定理から、システムは互換性のないシステム (IS) であると推定されます。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bb3fec88cf5c6d788afb4480ab1f58_l3.png)
したがって、 m=-1 の場合、連立方程式は互換性のない系であるため、解がありません。