オイラーの公式は、複素数と三角法という数学の 2 つの基本概念を結び付ける数学的概念です。このため、これは最も重要な概念化の 1 つであり、数学全体で最も多くの応用が可能です。この記事では、この式がどのようなものなのか、またその使用法をすべて見ていきます。
オイラーの公式とは何ですか?
オイラーの公式は、 オイラー数に基づく基本的な数学方程式であり、複素数を三角法に関連付けます。 18 世紀にスイスの数学者レオンハルト オイラーによって発見され、以来、物理学からコンピューター サイエンスに至るまで、さまざまな分野で使用されてきました。
オイラーの公式は e ix = cos(x) + i sin(x) と書きます。ここで、e は自然対数の底、i は虚数単位(-1 の平方根として定義)、x は実数です。番号。この方程式は、複素数 e ix が実数 cos(x) と虚数 i と実数 sin(x) の積の和に等しいことを指定します。

オイラーの公式の重要性は、複素数を実数と三角法の観点から表現できるようになり、操作と計算が容易になるという事実にあります。
オイラーの公式の証明
オイラーの公式の証明は、指数関数に対するテイラー級数の使用と、コサインとサインに対する三角関数の恒等式に基づいています。
まず、指数関数のテイラー級数を考えます。

次に、上記の方程式の x を ix に置き換えます。ここで、i は虚数単位 (-1 の平方根) です。
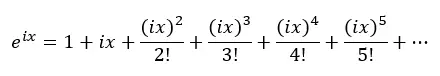
したがって、i のべき乗を適用して、前の式に代入します。
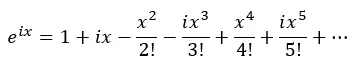
ここで、実項と i を含む項をグループ化します。
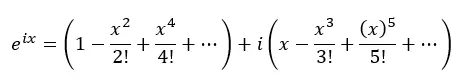
実際、上記の各括弧はコサインとサインのテイラー級数です。
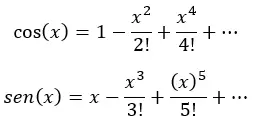
最後に、(括弧内の各式を x のコサインとサインに置き換えることによって) 簡略化すると、次のようになります。

オイラーの公式の例
この数式がどのように機能するかがわかったので、次の実際的な例を解いてみることをお勧めします。 複素数 e 2i (ラジアン単位)を二項形式で表します。
オイラーの公式の主な用途は、指数形式で表現された複素数を二項形式に変換することです。したがって、次の式を使用します: e ix = cos(x) + i sin(x)
e 2i = cos(2) + i sin(2)
e2i = -0.416 + 0.909i
そして、すでに二項形式の数値が得られています。そこから、複素平面でグラフィック表現を作成できます。そのためには、複素数は、横軸 (x 軸) の実部と縦軸 (y 軸) の虚部を座標として使用して複素平面で表現されることを理解する必要があります。
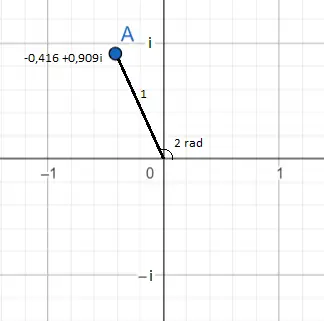
前の画像では、複素数 e 2iが示されています。これは -0.416 + 0.909i に等しくなります。これは青色の点として表示されます。平面上のその位置は2 つの角度から見ることができます。
最初の最も明白な方法は、数値を二項形式で表現したものです: -0.416 (横軸) と 0.909 (コンピューター上)。 2 番目は指数形式です。e 2iの加群は、e の前にある数値であるため 1 に等しくなります (e の前に数値がないので、1 があると想像する必要があります)。指数には 2 があるため、引数または角度は 2 ラジアンに相当します。
この最後の段落をよく理解していない場合は、複素数に関する記事を読むことをお勧めします。さて、そこでは、複素数を記述するさまざまな方法とそのすべてのプロパティについて、非常に詳細に説明しています。
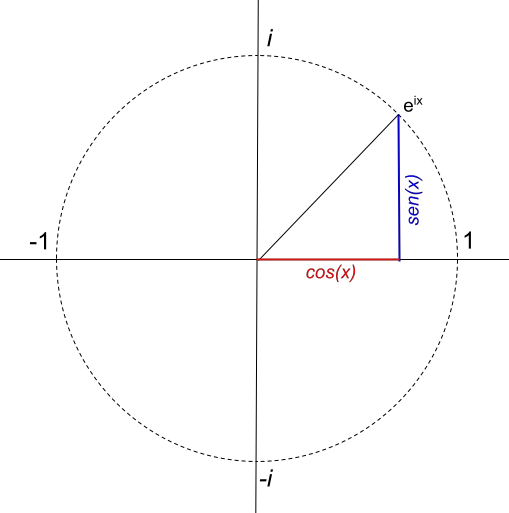
オイラーの公式のグラフ表示
前の例では、オイラーの公式がどのように適用され、それが複素平面でどのようにグラフィカルに表現されるかを確認できました。しかし、もう少し進んでオイラーの公式と同等の関数を表現しようとすると、非常に興味深いことがわかります。半径 1 の円が生成されます。
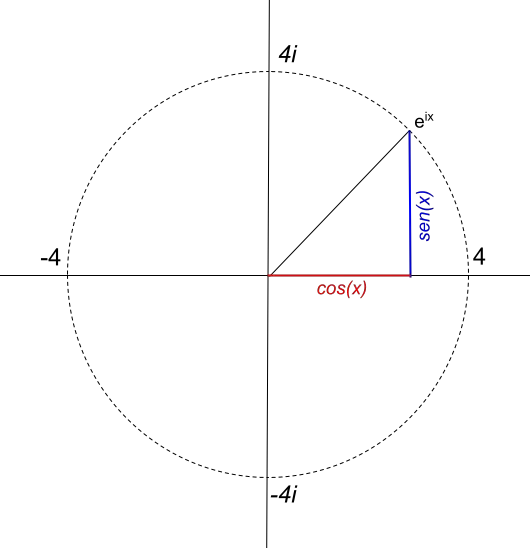
ただし、円の半径は複素数のモジュールの値に直接依存します。たとえば、半径 4 の円を表したい場合、関数は 4e ixになります。したがって、関数 4e ixは次のように表されます。
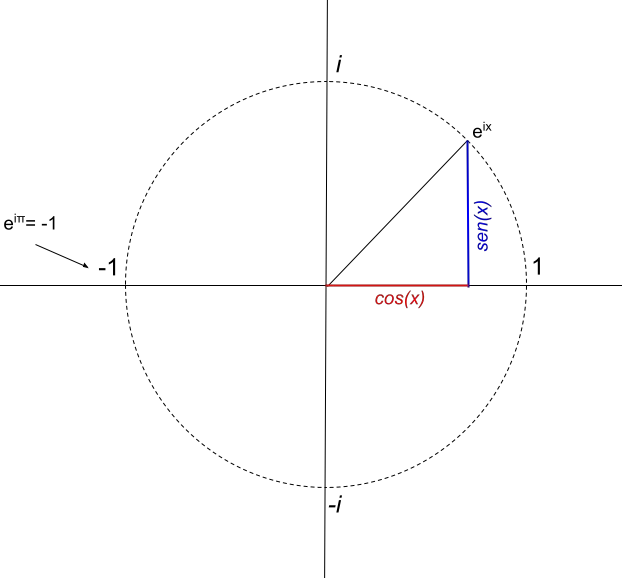
半径 1 の円に戻ると、e iπ (ラジアン単位) を表すことにした場合、最初に次のように計算する必要があります。
e πi = cos(π) + i sin(π)
eri = -1 + i 0
エリ= -1
e πi = -1 が得られます。これは有名なオイラー恒等式です。
これから、複素数 e πi には -1 に等しい実数部が 1 つだけあることが推測されます。したがって、その表現は次のようになります。
オイラーの公式の応用
- 複素数:オイラーの公式は、三角関数と複素数の関係です。この式から、複素数をさまざまな方法 (二項、指数、極) で表現できます。
- テイラー級数:オイラーの公式はテイラー級数関数を拡張するために使用されます。
- 線形代数:オイラーの公式は、線形代数の基本的な手法である行列の対角化で使用されます。
- 微積分および積分:オイラーの公式は、微積分に関連する手法である微分方程式の解法に使用されます。
さらに、多くの数学理論や、物理学の定理など、数学の領域外の概念にも応用できます。
結論
この記事で見てきたように、オイラーの公式の最大の応用は複素数、つまりその数値表現とその表現です。これが代数に応用できることは確かですが、本質的には複素数を扱うことになります。したがって、それらをよく理解することが何よりも重要です。
そうは言っても、この概念をよりよく理解するのに役立つことを願っています。質問がある場合、またはエクササイズの方法がわからない場合は、遠慮なくコメント欄に書いてください。