このページでは、座標系とは何かを説明し、さらにデカルト座標系についてすべて説明します。他のタイプの座標系 (極座標系、円筒座標系、球面座標系など) や座標系の実世界の応用例も紹介します。
座標系とは何ですか?
最初はこの概念を理解するのが少し難しいですが、座標系の定義は次のとおりです。
座標系は、点の位置を識別できるようにするシステムです。つまり、幾何学的オブジェクトの位置を定義するために使用される値のセットです。
たとえば、次の飛行機が飛行している位置は、次の座標系で表すことができます。
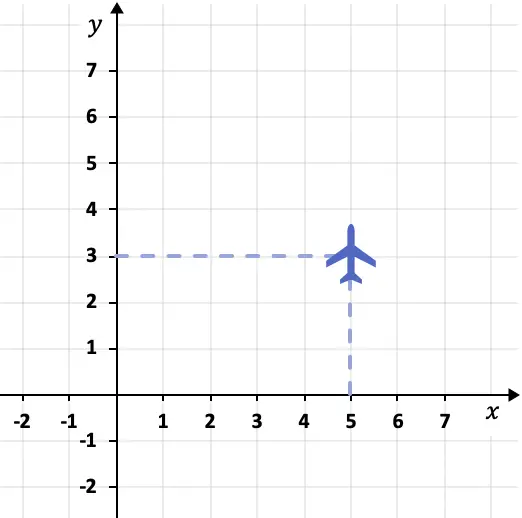
この場合、平面は点 (5.3) にあります。 X 座標が 5、Y 座標が 3 であるためです。
![]()
一方、点 (0,0) は、座標軸の開始点であり、座標系の基準点であるため、座標原点と呼ばれます。
好奇心からですが、座標系を発明した数学者はフランス人のルネ・デカルトであると考えられています。そのため、デカルト座標系とも呼ばれます。
平面内のデカルト座標系
前のセクションで見たグラフは、平面内のデカルト座標系に属しています。これが 2 次元システムであるため、平面内にあると言えます。つまり、X 軸と Y 軸の 2 つの軸しかありません。
X 軸は水平座標に対応し、Y 軸は垂直座標を表します。以下に、座標とともにグラフィカルに表現されたいくつかの点を示します。
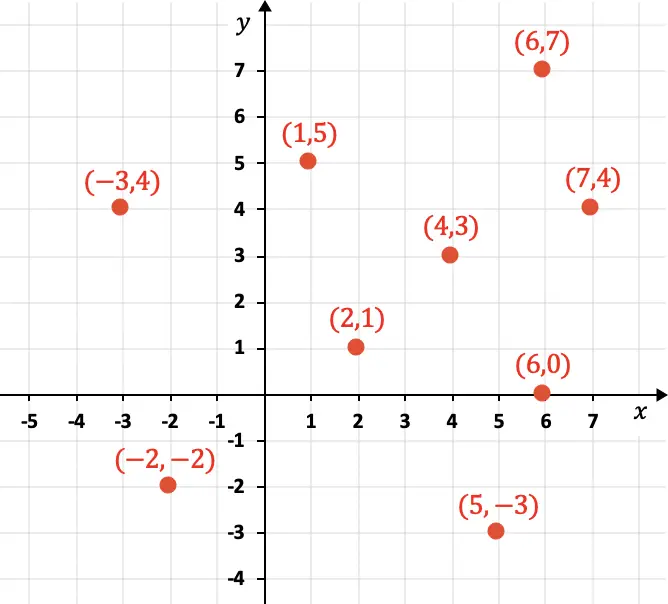
グラフからわかるように、座標は括弧で数値的に表され、さらに X コンポーネントが最初に配置され、次に Y コンポーネントが配置されます: (4,3)。さらに、座標は正、負、またはゼロにすることができます。
一方、このタイプの座標系はデカルト平面とも呼ばれます。
最後に、座標軸はすべて同じことを意味しますが、いくつかの言い方ができることを知っておく必要があります。
- X 軸は、横軸または OX 軸とも呼ばれます。
- Y 軸は、y 軸または OY 軸とも呼ばれます。
空間内のデカルト座標系
平面内、つまり 2 つの軸 (2 次元) を持つ座標系で点を表す方法を説明しました。しかし、現実は3次元(高さ、幅、奥行き)で構成されています。
したがって、ユークリッド幾何学では、3 次元空間は一般に、互いに垂直な 3 つの軸を持つ座標系で表されます。
- X 軸は深さを表します。
- Y 軸は幅を示します。
- Z 軸は高さに対応します。
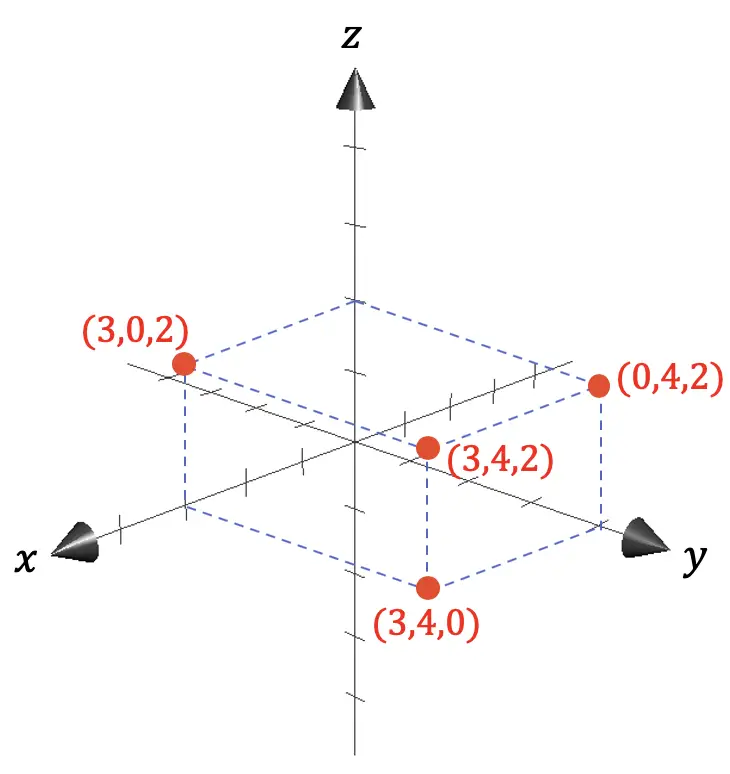
前のグラフ表示でわかるように、任意の点の座標は、問題の点と原点 (0,0,0) の間の距離の軸への投影によって与えられます。
極座標系
2D または 3D のデカルト座標系が最も広く使用されています。ただし、場合によっては、別のタイプの座標系を使用した方が便利な場合もあります。
極座標系は2 次元の参照系であり、その座標は次のとおりです。
-

座標原点と点の間の距離です。これを動径座標と呼びます。
-

点と原点を通る線と X 軸がなす角度です。これは角度座標または方位座標と呼ばれます。
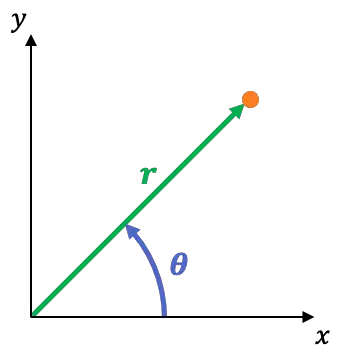
次の方程式を使用すると、直交座標系から極座標系に簡単に切り替えることができます。
極座標をデカルト座標に変換する
![]()
![]()
デカルト座標から極座標への切り替え
![]()
![]()
円筒座標系
円筒座標系は極座標系に非常に似ています。実際、これは同じことですが、もう 1 つの座標、つまり高さが異なります。
したがって、円筒フレームは 3 次元フレーム、つまり 3 つの座標を持ちます。
-

は、XY 平面内の点の正投影、つまり Z 軸からの点の距離です。
-

正の半軸が成す角度です

-

は点の高さであり、空間内のデカルト座標系の同じ座標です。
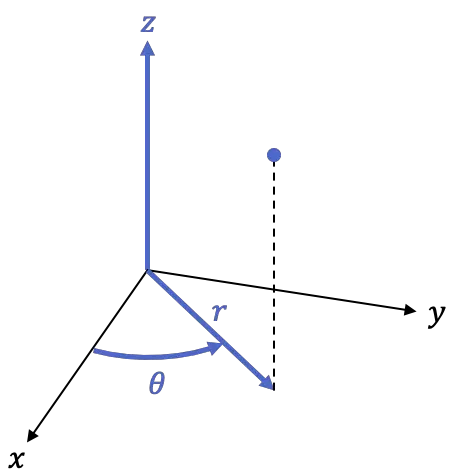
次の公式は、デカルト座標系を円筒座標に変換するために使用されます。
円筒座標をデカルト座標に変換する
![]()
![]()
![]()
デカルト座標を円筒座標に変換する
![]()
![]()
![]()
球面座標系
最後に、球面座標系があります。このタイプの座標系は極座標や円筒座標にもよく似ていますが、明らかにそれらとはいくつかの違いがあります。
球面座標系は3 次元ユークリッド空間を記述するためのシステムであるため、次の 3 つの座標があります。
-

原点から点までの距離 (R3 内の) です。
-

X 軸の正の部分が線となす角度です。

XY 平面に投影されます。
-
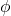
Z 軸の正の部分と直線の間の角度です。

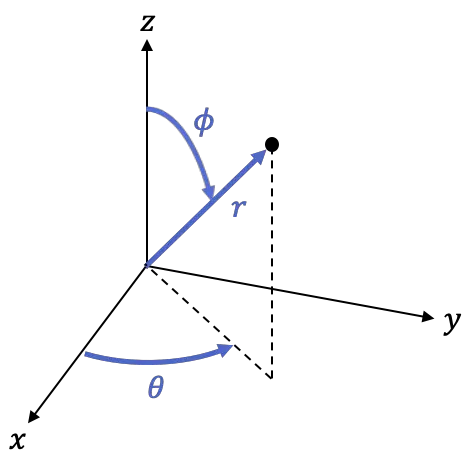
次の式を使用して、球面座標とデカルト座標を切り替えることができます。
球面座標をデカルト座標に変換する
![]()
![]()
![]()
デカルト座標を球座標に変換する
![]()
![]()
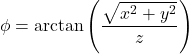
座標系の実世界への応用
座標系は実生活でも使用されるため、数学において非常に重要です。たとえば、地図上の物体、人、さらには場所の位置を特定するのに役立ちます。実際、GPS は座標系のおかげで存在します。地球上の位置を知るために GPS が使用されるからです。
より正確には、GPS 地理座標は緯度と経度の 2 つの要素で構成されます。緯度 (北または南) と経度 (東または西) は、地球の中心と現在地の間の角度を測定する 2 つの角度座標です。どちらも、10 進座標または 60 進座標の度で表されます。