この記事では、関数(式)のコセカントを求める方法を説明します。コセカントの導関数を段階的に解く練習問題も見つかります。そして最後に、このタイプの三角関数導関数の公式のデモンストレーションを見ることができます。
コセカント導関数の公式
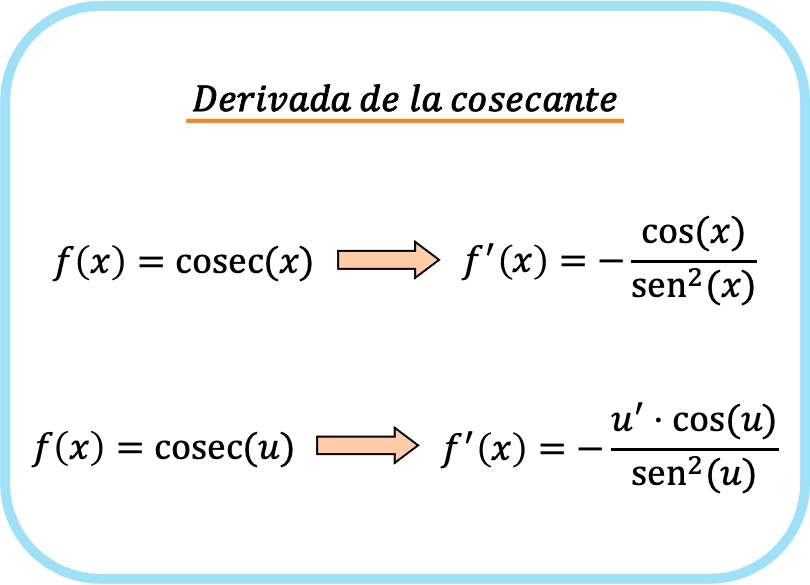
x の余割の導関数は、x の余弦を x の二乗正弦で割った商を引いたものに等しくなります。
![]()
三角関数の公式を使用すると、x のコセカントの導関数を、x のコタンジェントと x のコセカントの積を引いたものとして定義することもできます。
![]()
連鎖則を適用すると、関数のコセカントの微分値は、関数の微分値と関数のコサインの積を減算し、関数の正弦の 2 乗で割った値になります。
![]()
したがって、関数のコセカントを導出するために使用される式は次のようになります。
コセカントの導関数の例
コセカントの導関数の公式が何であるかを理解したので、次にいくつかの例を示します。したがって、関数の余割がどのように導出されるかを正確に確認できます。
例 1: 2x の余割の導関数
この例では、2x の余割の微分がどのくらいになるかを確認します。
![]()
コセカント引数関数は x とは異なるため、コセカント微分規則と連鎖規則を使用する必要があります。
![]()
したがって、この三角関数の導関数を求めるには、前の式の値を単純に置き換えます。コサインとサインの引数に 2x を入力し、u’ は 2x の導関数、つまり 2 に対応します。
![]()
例 2: x の 2 乗の余割の導関数
この演習では、x の 2 乗の余割の導関数がどのくらいになるかを確認します。
![]()
論理的には、この三角関数の導関数は、余割の導関数の公式を使用して解決されます。
![]()
x の 2 乗の導関数は 2x となるため、x のコセカントの 2 乗の導関数は次のようになります。
![]()
例 3: 指数関数の 3 乗余割の導関数
![]()
関数の引数が何であっても、関数の余割の導関数の規則は次のとおりです。
![]()
しかし、この場合、コセカントが 3 に累乗され、さらにその引数に指数関数があるため、複合関数になります。したがって、関数全体を区別するには、連鎖ルールを数回適用する必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ac2ce49dfcba1b7f27696dba0a2decb_l3.png)
コセカントの導関数の問題を解決しました
次の余割関数を導出します。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-32dde68d2a11ef6a05d483b26f0a98ef_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bea25dae467cefdcc1bd48e8d9bc88_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb70e1d7b6f2ce2636934b235904861f_l3.png)
コセカントの導関数の公式の証明
次に、余割の導関数の公式を示します。他のデモとは異なり、この場合は導関数を定義する制限を使用しませんが、コセカントの数学的定義から始めます。
代数的には、余割三角関数は正弦の乗法逆関数です。
![]()
したがって、商規則を使用して余割の導関数を求めることができます。
![]()
![]()
ご覧のとおり、割り算の導関数のルールを適用することによってのみ、コセカントの導関数の公式に到達します。また、商の導関数はすでに証明されているため (次のリンクで確認できます)、コセカント導関数則も証明されています。
➤参照:商の導関数の証明