▷ コサインの導関数（公式と演習問題）

ここでは、コサイン関数（公式）を導出する方法を学びます。コサイン関数の導関数の例を確認し、段階的な演習で練習することができます。さらに、式の証明、コサインの二次導関数、さらには逆コサインの導関数も示します。

コサインの導関数は何ですか?

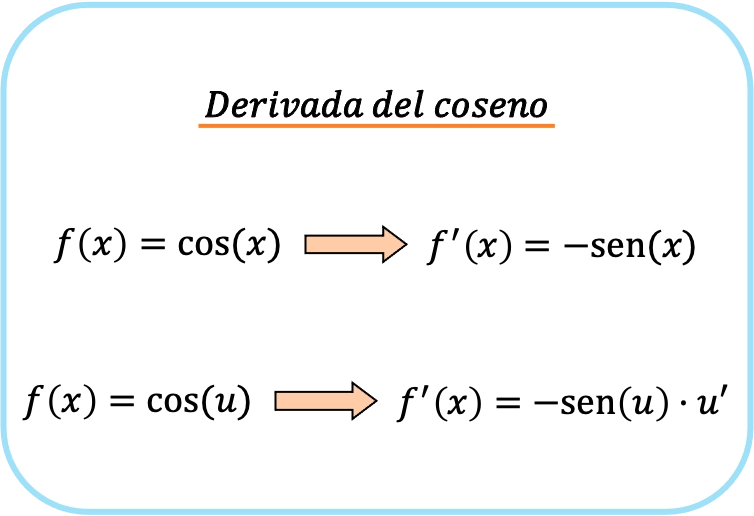
コサイン関数の導関数は、符号変更されたサイン関数です。言い換えれば、x のコサインの導関数は、x のサインを引いたものに等しくなります。

$f(x)=\text{cos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x)$

コサイン引数に関数がある場合、コサインの導関数は、その関数のサインを引いた値と関数の導関数を掛けた積になります。

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

2 番目の式は最初の式と同等ですが、連鎖規則を適用します。つまり、コサインの導関数の公式は次のようになります。

コサイン導関数の例

コサイン公式が何であるかを理解したところで、コサイン関数の導出方法について疑問がなくなるように、このタイプの三角関数の導関数の例をいくつか説明します。

例 1: 2x のコサインの導関数

$f(x)=\text{cos}(2x)$

コサイン引数には単一の x はなく、より複雑な関数が含まれています。したがって、次の式を使用してコサインを導出する必要があります。

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

2x の導関数は 2 であるため、2x のコサインの導関数は、2x のサインを 2 倍した値を引いたものになります。

$f(x)=\text{cos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(2x)\cdot 2=-2\text{sen}(2x)$

例 2: x の 2 乗の余弦の導関数

$f(x)=\text{cos}(x^2)$

前の例と同様に、コサイン引数には x とは異なる関数があるため、連鎖規則を使用してコサインを導出します。

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

この場合、x ²の導関数は 2x となるため、x のコサインの 2 乗の導関数は次のようになります。

$f(x)=\text{cos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x^2)\cdot 2x$

例 3: 3 乗コサインの導関数

$f(x)=\text{cos}^3(2x^6-5x^3)$

この例のコサイン関数は別の関数で構成されているため、導関数を解くには次の公式を適用する必要があります。

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

したがって、式を適用すると、関数の導関数が得られます。

$\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}$

➤この関数を微分するには、ポテンシャル関数の導関数の公式も使用する必要があります。

コサインの二次導関数

次に、三角関数の性質により、sin の 2 階微分が簡単に計算できることを見てみましょう。

➤注:以下の内容を理解するには、 sine の導関数が何であるかを知る必要があります。

x のコサインの 2 階導関数は、x のコサインを引いたものです。奇妙に思われるかもしれませんが、数学的にはそのようです。実際、サインの導関数はコサインなので、x のコサインを 2 回微分すると、符号が変更されたコサインが再び得られます。

$\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}$

このプロパティは、コサイン引数が x でない場合に変化します。この場合、連鎖ルールの項をドラッグするためです。

$\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}$

逆余弦の導関数

すべての三角関数には逆関数があり、コサイン関数も逆関数になります。同様に、逆余弦は微分可能です。

関数の逆余弦の微分値は、関数の微分値を 1 の平方根で割った値から、関数の 2 乗を引いた値を引いたものです。

$f(x)=\text{cos}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

逆余弦は逆余弦とも呼ばれることを覚えておいてください。

たとえば、3x の逆余弦の導関数は次のようになります。

$f(x)=\text{cos}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3}{\sqrt{1-(3x)^2}}=-\cfrac{3}{\sqrt{1-9x^2}}$

コサインの微分に関する演習を解決しました

次のコサイン関数の導関数を計算します。

$\text{A) } f(x)=\text{cos}(4x)$

$\text{B) } f(x)=\text{cos}(2x^3-5x+1)$

$\text{C) } \displaystyle f(x)=9\text{cos}\left(\frac{x}{3}\right)$

$\text{D) } f(x)=\text{cos}^5(x^2+3x)$

$\text{E) } f(x)=\text{cos}\left(e^{5x}\right)$

$\text{F) } \displaystyle f(x)=9\text{cos}\left(\frac{e^x}{5x}\right)$

解決策を見る

$\text{A) } f'(x)=-\text{sen}(4x)\cdot 4 =-4\text{sen}(4x)$

$\text{B) } f'(x)=-\text{sen}(2x^3-5x+1)\cdot (6x^2-5)$

$\text{C) } \displaystyle f'(x)=-9\text{sen}\left(\frac{x}{3}\right)\cdot \frac{1}{3} =-3\text{sen}\left(\frac{x}{3}\right)$

$\text{D) } f'(x)=-5\text{cos}^4(x^2+3x)\cdot \text{sen}(x^2+3x)\cdot (2x+3)$

$\text{E) } f'(x)=-\text{sen}\left(e^{5x}\right)\cdot e^{5x}\cdot 5=-5\text{sen}\left(e^{5x}\right)\cdot e^{5x}$

$\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}$