L’intérêt simple est le moyen le plus courant de calculer les intérêts, et il est utilisé à diverses fins, de l’achat d’une maison à l’obtention d’un prêt personnel. Si jamais vous avez besoin de calculer des intérêts simples, ce guide vous montrera comment le faire étape par étape. Aussi, nous mettons à votre disposition un calculateur en ligne pour vous faciliter la tâche.
Calculateur d’intérêts simple
Ce calculateur d’intérêt simple en ligne est un outil qui peut vous aider à calculer l’une des variables impliquées dans le calcul de l’intérêt simple. Pour l’utiliser, il vous suffit de sélectionner ce que vous voulez calculer et d’entrer les données des variables qu’il demande. Ensuite, vous devez cliquer sur le bouton calculer et c’est tout.
Qu’est-ce que l’intérêt simple ?
L’intérêt simple est le taux d’intérêt appliqué lorsque vous investissez ou prêtez un montant pour une période de temps déterminée. Il est calculé en multipliant le montant initial par le taux d’intérêt et le temps. En résumé, cet intérêt est utilisé dans des actions financières constantes et normalement de courte durée.
Étant donné que le taux d’intérêt et la période de temps sont maintenus constants, les intérêts qui doivent être payés mensuellement ou annuellement sont toujours les mêmes , puisque les intérêts ne s’accumulent pas. C’est la principale différence entre l’intérêt simple et l’intérêt composé .
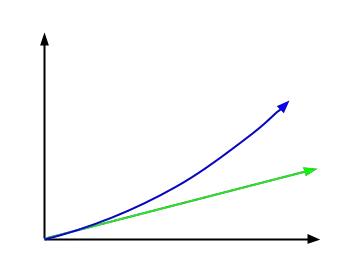
Dans l’image suivante, vous pouvez voir en vert la fonction qui représente l’intérêt simple et la fonction d’intérêt composé, représentée en bleu. Comme on peut le voir sur l’image, il a une forme beaucoup plus exponentielle .
Formule pour calculer l’intérêt simple
La formule pour calculer l’intérêt simple est : I = C xixt , dans laquelle interviennent les variables suivantes :
- Capital initial (C) : somme d’argent investie ou prêtée, sur laquelle sont calculés des intérêts simples.
- Taux d’intérêt (i) : cet indicateur nous indique en pourcentage le montant des intérêts par rapport au temps. Il est important de l’écrire autant par un dans la formule (divisez la valeur en pourcentage par cent).
- Temps (t) : La durée de la période d’investissement, généralement exprimée en années. Bien que, ci-dessous, nous vous apprendrons comment le convertir en d’autres unités de temps, telles que : mois et jours.
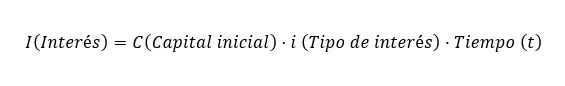
Pour voir comment cette formule est utilisée, on peut considérer l’ exemple suivant : nous avons 1000€ investis à un taux annuel de 4%, au bout de trois ans, combien d’intérêts aurons-nous générés ? Pour trouver les intérêts générés, nous devons appliquer la formule : I = C x (i ÷ 100) xt = 1000 x (4 ÷ 100) x 3 = 120 €.
Ensuite, à partir de la formule principale, on peut isoler les différentes variables et ainsi, on obtient les formules qui permettent de calculer le capital initial, le taux d’intérêt, le temps et le capital final. Et c’est ce que nous verrons dans les sections suivantes, où nous vous apprendrons comment calculer ces variables à partir de la formule que vous avez déjà vue et d’une autre très simple.
Comment est calculé le capital final ?
Pour calculer le capital final , il suffit d’appliquer la logique. Ensuite, puisque le montant final est égal au montant initial, une fois qu’on a appliqué les intérêts, sa formule est : Capital final (Cf) = Capital initial (C) + Intérêts (I). Cette expression est la deuxième formule d’intérêt simple la plus importante, la plus importante étant la précédente.
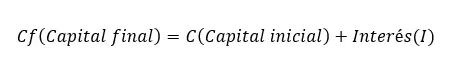
Maintenant que vous connaissez la formule, essayez de résoudre cet exemple pratique : Quel est le capital final que vous obtiendrez si vous investissez 50 000 € pendant 4 ans, avec un intérêt de 20 000 € ? Simplement, on applique l’ expression d’avant : Capital final (Cf) = Capital initial (C) + Intérêt (I) = 50 000 + 20 000 = 70 000 €.
Comment est calculé le capital initial ?
Si nous voulons calculer le capital initial, nous pouvons utiliser deux formules, en fonction des données qu’elles nous donnent. Dans un premier temps, on peut appliquer l’expression de la section précédente si l’on dispose du capital final et du montant généré par les intérêts : Capital initial (C) = Capital final (Cf) – Intérêts (I).
Deuxièmement, nous pouvons isoler la valeur du capital initial dans la formule d’intérêt simple (celle dont nous avons parlé au début). Il nous resterait donc Capital initial (C) = Intérêt (I) ÷ (Temps (t) x Taux d’intérêt (i)).

Voyons un exemple du deuxième cas, plus complexe : Combien dois-je investir pour obtenir des intérêts sur 30 000 €, avec un taux de 8 % pendant 2 ans ? Nous appliquons la formule Capital initial = I ÷ (tx (i ÷ 100)), ce qui nous laisse avec 30 000 ÷ (2 x (8 ÷ 100)) = 187 500 € initial.
Comment est calculé le taux d’intérêt ?
Pour calculer le taux d’intérêt , nous devons également utiliser la formule d’intérêt simple, mais en isolant le i. Par conséquent, il nous reste : Taux d’intérêt (i) = Intérêt (I) ÷ (Capital initial (C) x Temps (t)). Comme vous pouvez le voir, toutes les formules sont les mêmes, mais en isolant une variable différente.
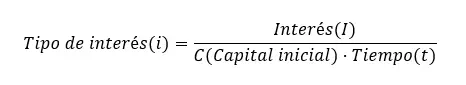
Voici un cas pratique de calcul de taux d’intérêt : A quel taux d’intérêt faut-il investir 180 000 € pendant 5 ans, si on veut le convertir en 200 000 € ? Dans cet exemple, il faut d’abord trouver l’intérêt : I = Cf – C = 200 000 – 180 000 = 20 000 €. Et puis nous résolvons : Taux d’intérêt = 20 000 ÷ (180 000 x 5) = 0,022 x 100 = 2,2 %.
Comment le temps est-il calculé ?
Enfin, nous pouvons calculer le temps , qui peut également être obtenu à partir de la formule initiale : Temps (t) = Intérêt (I) ÷ (Montant initial (C) x Taux d’intérêt (i)). Il est important de se rappeler que la formule exige que les unités de temps soient des années. Cependant, si vous souhaitez l’exprimer dans d’autres unités, vous pouvez utiliser les variantes suivantes de la formule :
- I = C · (i / 100) · t si t sont des années (Formule Générale)
- I = C · (i / 1200) · t si t sont des mois (Résultat en mois)
- I = C · (i / 36000) · t si t sont des jours (Résultat en jours)
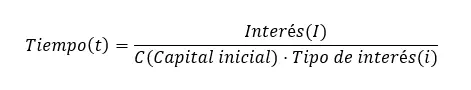
Regardez l’exemple suivant : Combien de temps doit s’écouler si on veut qu’un investissement de 40 000 € génère un intérêt de 5 000 €, avec un taux de 5 % ? Le calcul reste : Temps = 5 000 ÷ (40 000 x 5 ÷ 100) = 2,5 ans. Cependant, si nous voulons le calculer en mois, nous pouvons faire ce qui suit : Temps = 5 000 ÷ (40 000 x 5 ÷ 1200) = 30 mois.
Exemple réel de calcul d’intérêt simple
Vous avez maintenant vu un exemple de calcul de chaque variable qui compose la formule d’intérêt simple. Cependant, nous voulons vous montrer un dernier exemple du calcul le plus courant , qui est celui de l’intérêt lui-même. Avec lequel appliquer la première formule, vous aurez des restes. Au cas où vous souhaiteriez revoir le calcul, voici une étude de cas :
Nous empruntons 10 000 € pour investir et nous voulons calculer combien d’argent nous devrons rembourser après 5 ans s’ils nous demandent 3 % d’intérêts annuels. Le calcul serait :
10 000 x 0,03 = 300
300 x 5 ans = 1 500 €
CF = 10 000 € + 1 500 € = 11 500 €
Ainsi, au bout des 5 ans les intérêts seraient de 1 500 € et le capital final à verser serait de 11 500 € .
conclusion
En résumé, pour calculer les intérêts simples , il faut tenir compte du montant du prêt, du taux d’intérêt et de la durée. À partir de là, il vous suffit de multiplier ces trois nombres pour obtenir le montant total des intérêts à payer. Et si vous voulez calculer l’une des autres variables, au lieu de l’intérêt, il vous suffit d’isoler cette valeur dans la formule générale.